LeetCode刷题17:深度优先搜索解决547. 省份数量

有?n?个城市，其中一些彼此相连，另一些没有相连。如果城市?a?与城市?b?直接相连，且城市?b?与城市?c?直接相连，那么城市?a?与城市?c?间接相连。

省份?是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个?n x n?的矩阵?isConnected?，其中?isConnected[i][j] = 1?表示第?i?个城市和第?j?个城市直接相连，而?isConnected[i][j] = 0?表示二者不直接相连。

返回矩阵中?省份?的数量。

示例 1：

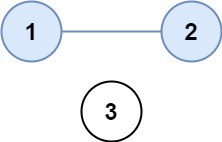
输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]

输出：2

示例 2：

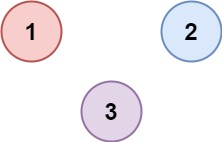
输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]

输出：3

提示：

• 1 <= n <= 200
• n == isConnected.length
• n == isConnected[i].length
• isConnected[i][j]?为?1?或?0
• isConnected[i][i] == 1
• isConnected[i][j] == isConnected[j][i]

思路解析：

? ? ? 由题我们可以看出该题就是图的应用，我们可以把示例中的输入看成图的邻接矩阵表达方式，而题目表示一个省份是直接或间接相连的，我们可以把那么连一块的节点看做一个省份，这样不难看出这是图的深度优先遍历方法的应用。

因此，我们就用常规方法深搜遍历图，计算出所有省份即可

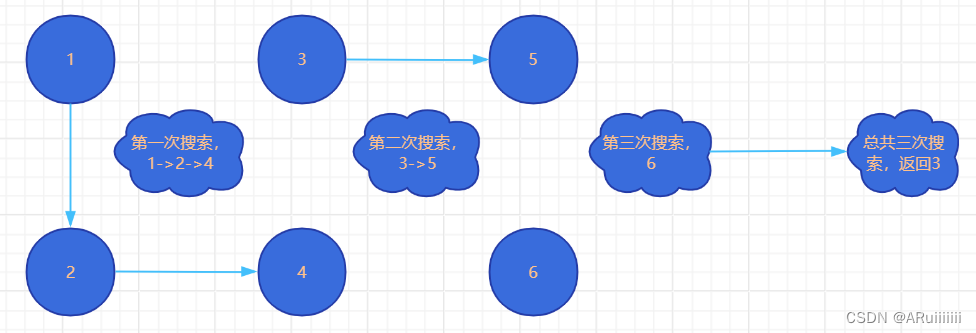
图示深度优先遍历过程：

输入：isConnected =

[[1,1,0,0,0,0],

[1,1,0,1,0,0],

[0,0,1,0,1,0],

[0,1,0,1,0,0],

[0,0,1,0,1,0],

[0,0,0,0,0,1]]

从下标1开始：

?代码实现：

class Solution {
    //boolean数组判断节点是否访问过
    boolean []isvisited;
    public int findCircleNum(int[][] isConnected) {
        int num=0;
        isvisited=new boolean[isConnected.length];
        //循环遍历节点，若访问过则跳过
        for(int x=0;x<isConnected.length;x++){
            if(!isvisited[x]){
                //每次进行搜索，num+1
                num++;
                dfs(x,isConnected);
            }
        }
        return num;
    }
    //进行深度优先搜索
    public void dfs(int n,int[][] isConnected){
        for(int x=0;x<isConnected[0].length;x++){
            if(isConnected[n][x]==1&&!isvisited[x]){
                isvisited[x]=true;
                dfs(x,isConnected);
            }
        }
    }
}