【算法与数据结构】62、LeetCode不同路径

所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。

一、题目

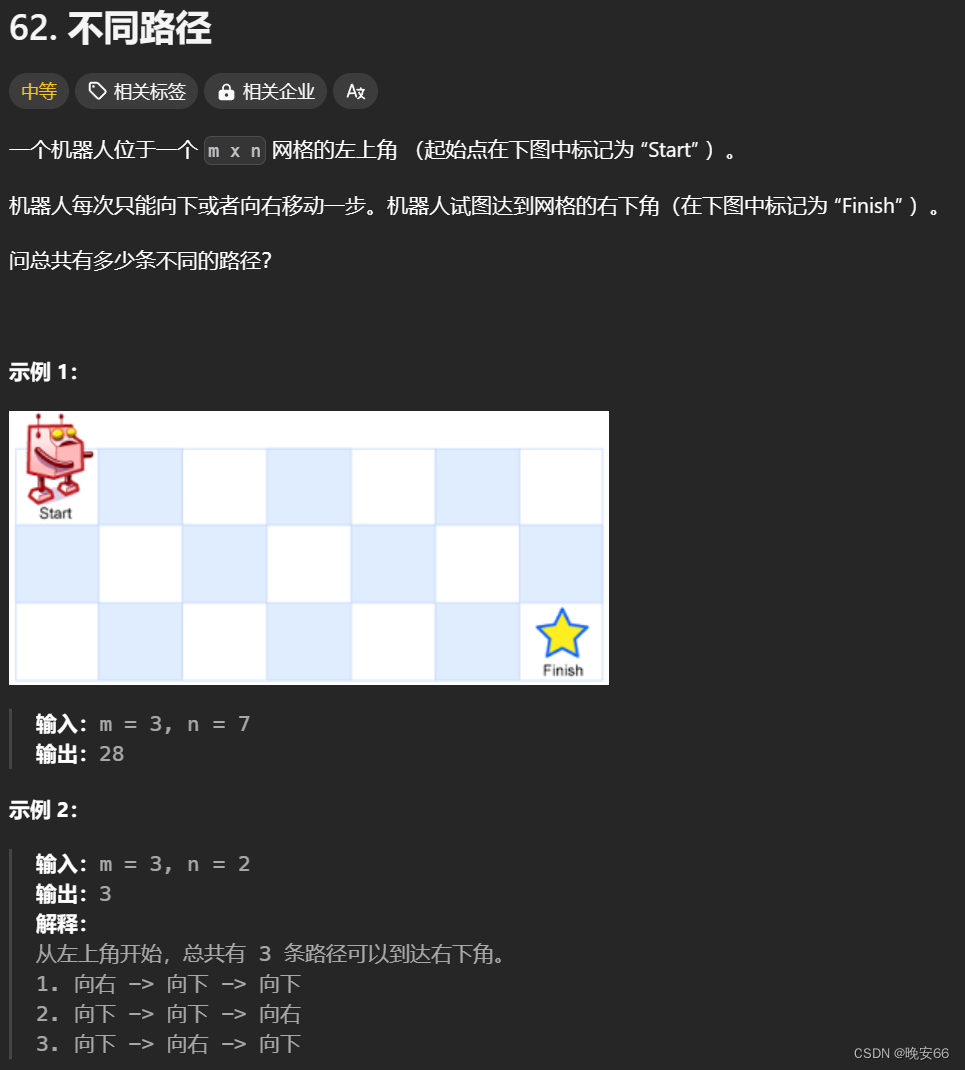
二、解法

??思路分析：机器人只能向下或者向右移动，那么到达（i,j）位置的路径和（i-1,j）以及(i,j-1)有关。那么我们就得到的动态规划的表达式$dp[i][j]=dp[i?1][j]+dp[i][j?1]$。其中，因为到达第一行和第一列位置的路径只有一条，因此dp数组中第一行第一列的元素都为1。根据如上信息，我们写出如下代码。
??程序如下：

class Solution {
public:
	int uniquePaths(int m, int n) {
		vector<vector<int>> dp(m, vector<int>(n, 1));
		for (int i = 1; i < m; i++) {
			for (int j = 1; j < n; j++) {
				dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
			}
		}
		return dp[m - 1][n - 1];
	}
};

复杂度分析：

• 时间复杂度： $O(m?n)$。
• 空间复杂度：$O(m?n)$。

三、完整代码

# include <iostream>
# include <vector>
using namespace std;

class Solution {
public:
	int uniquePaths(int m, int n) {
		vector<vector<int>> dp(m, vector<int>(n, 1));
		for (int i = 1; i < m; i++) {
			for (int j = 1; j < n; j++) {
				dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
			}
		}
		return dp[m - 1][n - 1];
	}
};

int main() {
	int m = 3, n = 2;
	Solution s1;
	int result = s1.uniquePaths(m, n);
	cout << result << endl;
	system("pause");
	return 0;
}

end