信号的互相关计算及时延估计

1. 信号的互相关计算

互相关反映向量x和移位（滞后）向量y之间的相似性。

最直观的解释是：互相关的作用是为了找到信号在哪一时刻与另一信号最像（另一信号为本身时就是自相关）！

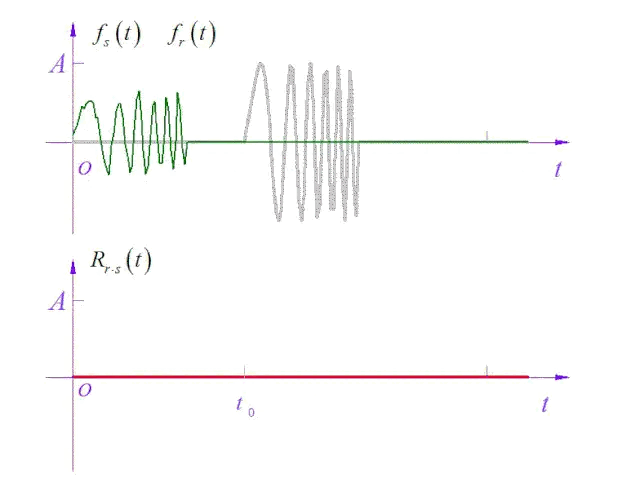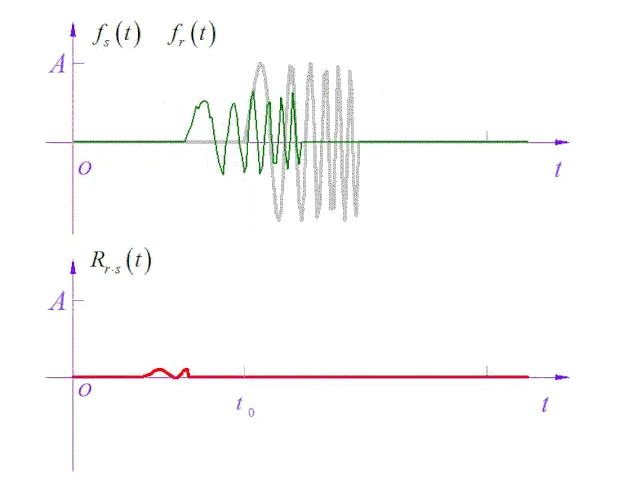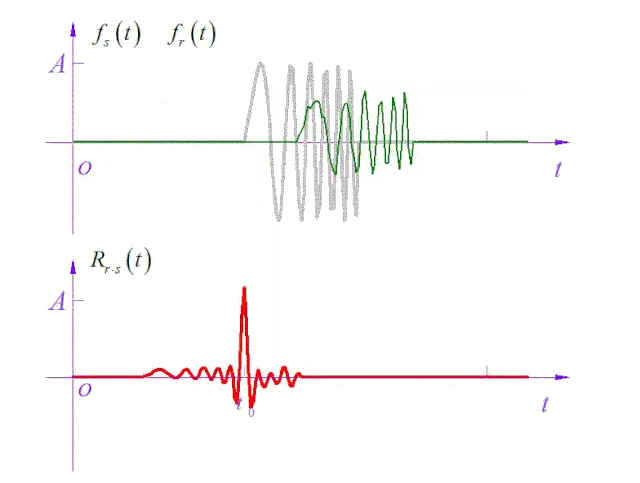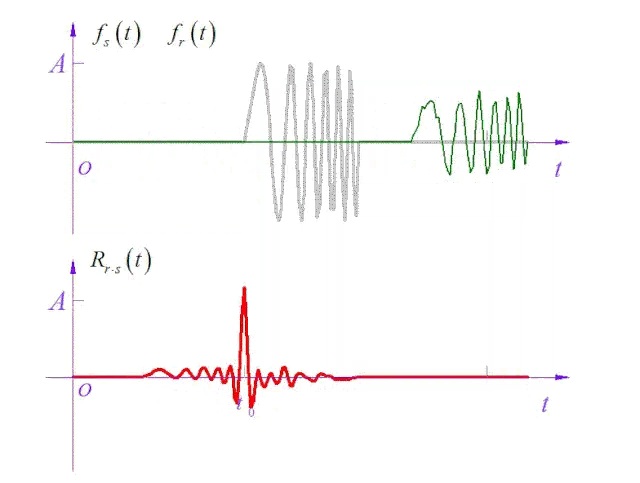
滑动求互相关（图片来源：卓晴老师）

互相关和自相关在本质上是两个函数做内积运算。即向量内积的连续形式。其在线性空间角度上的意义是：一个向量在另一个向量上的投影，内积结果越大，投影越大，两个向量间夹角越小，方向越一致，相似度越高。

互相关（Cross-Correlation）计算公式：
$$f(t)?g(t)={\int }_{?\infty }^{\infty }f(\tau )g(t+\tau )d\tau$$

离散形式：
$$f(t)?g(t)=\sum _{?\infty }^{\infty }f(t)g(t+\tau )d\tau$$

博主ccwcc给出的图片很形象的描述了这个计算过程。

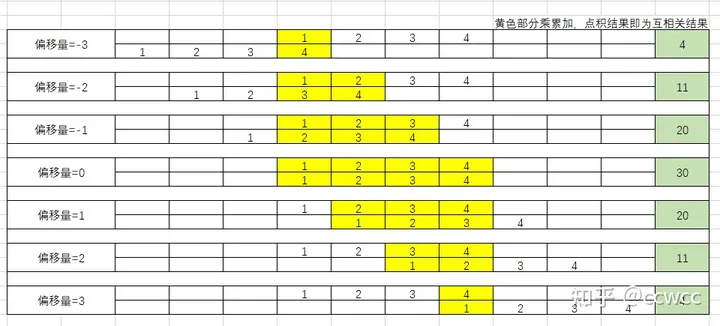
注意： 如果x和y的长度不同，函数会在较短向量的末尾添加0，使其长度与另一个向量相同。

时域和频域的求解方法如下：

clear,clc,close all
load xcorr_test.mat

xc = xcorr(x,y);
xc1 = xcorr_method1(x,y);
xc2 = xcorr_method2(x,y);
length(x)
length(y)
length(xc)
plot(xc)
hold on
plot(xc1)
plot(xc2)
legend

function corr_ = xcorr_method1(x,y)
    iDataN = length(x);
    iSyncLength = length(y);
    if iDataN > iSyncLength
        tmp = zeros(iDataN - iSyncLength,1);
        y = [y;tmp];
        len = iDataN;
    else
        tmp = zeros(iSyncLength-iDataN,1);
        x = [x;tmp];
        len = iSyncLength;
    end

    % 时域法
    N = len;
    corr_ = zeros(2*N-1,1);
    m = 0;
    for i = -(N-1):N-1
        m = m+1;
        for t = 1:N
            if 0<(i+t)&&(i+t)<=N
                corr_(m) = corr_(m) + y(t)*x(t+i);
            end 
        end
    end
end

function corr_ = xcorr_method2(x,y)

    iDataN = length(x);
    iSyncLength = length(y);
    if iDataN > iSyncLength
        tmp = zeros(iDataN - iSyncLength,1);
        y = [y;tmp];
    else
        tmp = zeros(iSyncLength-iDataN,1);
        x = [x;tmp];
    end

    % 频域法
    Nfft = length(x)+length(y)-1;
    corr_ = fftshift(ifft(fft(x,Nfft).*conj(fft(y,Nfft))));
end

2. 信号的时延估计

两个信号最相似时，相当于求自相关系数，此时类似求自身模长。

因此可用这一特性，求解时延周期。

xc = xcorr(x, y);
[peaks, locs] = findpeaks(xc);
[~, idx_] = max(peaks);
delay = locs(idx_) - length(x);

• 若delay > 0，则信号y滞后于信号x
• 若delay = 0，则信号x与信号y之间无时延
• 若delay < 0，则信号y超前于信号x

---

参考链接：

• https://zhuanlan.zhihu.com/p/71930587
• https://zhuanlan.zhihu.com/p/613949451
• https://blog.csdn.net/qq_45732223/article/details/109729960