机器学习 | K-means聚类

K-means聚类

基本思想

图中的数据可以分成三个分开的点集(称为族)，一个能够分出这些点集的算法，就被称为聚类算法

算法概述

K-means算法是一种无监督学习方法，是最普及的聚类算法，算法使用个没有标签的数据集，然后将数据聚类成不同的组K-means算法具有一个迭代过程，在这个过程中，数据集被分组成若干个预定义的不重叠的聚类或子组，使簇的内部点尽可能相似，同时试图保持簇在不同的空间，它将数据点分配给簇，以便簇的质心和数据点之间的平方距离之和最小，在这个位置，簇的质心是簇中数据点的算术平均值。

距离度量

详细可以看我之前的博客 度量距离
闵可夫斯基距离(Minkowski distance)

• 闵氏空间指狭义相对论中由一个时间维和三个空间维组成的时空，为俄裔德国数学家闵可夫斯基(H.Minkowski,1864-1909)最先表述。他的平坦空间(即假设没有重力，曲率为零的空间)的概念以及表示为特殊距离量的几何学是与狭义相对论的要求相一致的。闵可夫斯基空间不同于牛顿力学的平坦空间。$p$取1或2时的闵氏距离是最为常用的，$p=2$即为欧氏距离，而$p=1$时则为曼哈顿距离。

当$p$取无穷时的极限情况下，可以得到切比雪夫距离。
距离公式：

$$d\left(x,y\right)={\left(\sum _i|x_i?y_i{|}^p\right)}^{\frac{1}{p}}$$

K-means算法流程

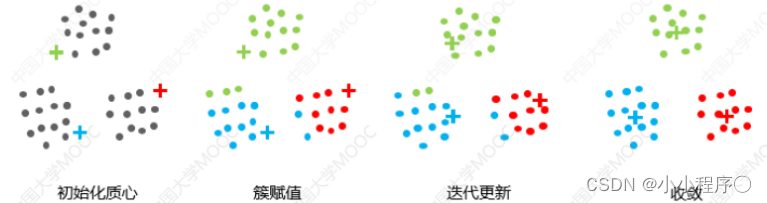
• 1.选择K个点作为初始质心。（初始化时，必须注意簇的质心必须小于训练数据点的数目。因为该算法是一种迭代算法，接下来的两个步骤是迭代执行的。）
• 2.将每个点指派到最近的质心，形成K个簇.（初始化后，遍历所有数据点，计算所有质心与数据点之间的距离。现在，这些簇将根据与质心的最小距离而形成。）
• 3.对于上一步聚类的结果，进行平均计算，得出该簇的新的聚类中心.（移动质心，因为上面步骤中形成的簇没有优化，所以需要形成优化的簇。为此，我们需要迭代地将质心移动到一个新位置。取一个簇的数据点，计算它们的平均值，然后将该簇的质心移动到这个新位置。对所有其他簇重复相同的步骤。）
• 4.重复上述两步/直到迭代结束: 质心不发生变化。（上述两个步骤是迭代进行的，直到质心停止移动，即它们不再改变自己的位置，并且成为静态的。旦这样做，k-均值算法被称为收敛。）
• 收敛函数
  
  

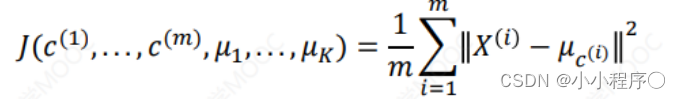
K值的选择

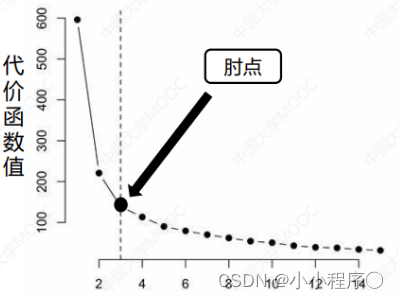
现在我们需要找到簇的数量。通常通过“时部法则”进行计算。我们可能会得到一条类似于人的时部的曲线。右图中，代价函数的值会迅速下降在K = 3的时候达到一个时点。在此之后，代价函数的值会就下降得非常慢，所以，我们选择K = 3。这个方法叫“时部法则”

K-means的优点

1. 原理比较简单，实现也是很容易，收敛速度快
2. 聚类效果较优。
3. 算法的可解释度比较强
4. 主要需要调参的参数仅仅是簇数K

K-means的缺点

• 需要预先指定簇的数量
• 如果有两个高度重叠的数据，那么它就不能被区分，也不能判断有两个簇
• 欧几里德距离可以不平等的权重因素限制了能处理的数据变量的类型
• 无法处理异常值和噪声数据
• 不适用于非线性数据集:
• 对特征尺度敏感-
• 如果遇到非常大的数据集，那么计算机可能会崩溃。
• 有时随机选择质心并不能带来理想的结果;

到这里，如果还有什么疑问欢迎私信、或评论博主问题哦，博主会尽自己能力为你解答疑惑的！
如果对你有帮助，你的赞和关注是对博主最大的支持！！
下次我将准备实现K-means算法