LeetCode、875. 爱吃香蕉的珂珂【中等，最小速度二分】

前言

博主介绍：?目前全网粉丝2W+，csdn博客专家、Java领域优质创作者，博客之星、阿里云平台优质作者、专注于Java后端技术领域。

涵盖技术内容：Java后端、算法、分布式微服务、中间件、前端、运维、ROS等。

博主所有博客文件目录索引：博客目录索引(持续更新)

视频平台：b站-Coder长路

---

LeetCode、875. 爱吃香蕉的珂珂【中等，最小速度二分】

来源：LeetCode专题《LeetCode 75》

题目及分类

题目链接：LeetCode、875. 爱吃香蕉的珂珂

类型：基础算法/二分

---

思路分析及代码实现

思路：

本题说让我们找到一个最少的每小时吃的香蕉数可以正好在有限时间内吃完，可以看到给我们的用例中数据量特别大，我们不可能将所有的每小时速度都去尝试模拟跑一遍，那么绝对会超时，我们选择好相应的左、右边界，然后来进行尝试二分处理。

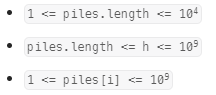
代码：

复杂度分析：时间复杂度O(n)；空间复杂度O(1)

class Solution {

    //对吃的最小速度进行二分
    //1000个位置 每个位置上限为亿
    public int minEatingSpeed(int[] piles, int h) {
        int l = 1, r = 1000000010;
        while (l < r) {
            int mid = (l + r) / 2;
            if (check(mid, piles, h)) r = mid;
            else l = mid + 1;
        }
        return l;
    }

    //check可以吃完，可以吃完返回true
    public boolean check (int k, int[] piles, int h) {
        int hh = 0;
        for (int i = 0; i < piles.length; i ++) {
            int curPile = piles[i];
            if (k >= curPile) hh ++;
            else hh += (int)Math.ceil(1.0 * curPile / k); //对于curPile / k可能会得到double类型，那么我们这里就需要提前*1.0让其变成浮点数
            if (hh > h) return false;
        }
        // if (k == 3) System.out.println(hh);
        return h >= hh ? true : false;
    }
}

代码优化

尝试优化，缩小左右边界：

①优化1：计算总和及某个元素最大值

long sum = 0;
int max = piles[0];
for (int pile: piles) {
    sum += pile;
    max = Math.max(max, pile);
}
//设置边界值
int l = (int)(sum / h), r = max;

原因：因为我们只是取所有数组中最大的那个元素，那么一旦我们数组中某个元素特别大，那么就会导致我们预想的直接失效。

②优化2：适当缩减右边界，提升效率

class Solution {

    //对吃的最小速度进行二分
    //1000个位置 每个位置上限为亿
    public int minEatingSpeed(int[] piles, int h) {
        int n = piles.length;
        long sum = 0;
        for (int pile: piles) {
            sum += pile;
        }
        //设置边界值  对于r尽可能相对大一些（我们将小时数尽量减小，这样就可以相对拉大速度，扩展右边界）
        int l = (int)(sum / h), r = (int)(sum / (h - n + 1) + 1);
        // System.out.printf("l=%d, r=%d\n", l, r);
        //进行二分
        while (l < r) {
            int mid = (l + r) / 2;
            if (check(mid, piles, h)) r = mid;
            else l = mid + 1;
        }
        return l;
    }

    //check可以吃完，可以吃完返回true
    public boolean check (int k, int[] piles, int h) {
        int hh = 0;
        for (int i = 0; i < piles.length; i ++) {
            int curPile = piles[i];
            if (k >= curPile) hh ++;
            else hh += (int)Math.ceil(1.0 * curPile / k); //对于curPile / k可能会得到double类型，那么我们这里就需要提前*1.0让其变成浮点数
            if (hh > h) return false;
        }
        // if (k == 3) System.out.println(hh);
        return h >= hh ? true : false;
    }
}

---

资料获取

大家点赞、收藏、关注、评论啦~

精彩专栏推荐订阅：在下方专栏👇🏻

• 长路-文章目录汇总（算法、后端Java、前端、运维技术导航）：博主所有博客导航索引汇总
• 开源项目Studio-Vue—校园工作室管理系统(含前后台，SpringBoot+Vue)：博主个人独立项目，包含详细部署上线视频，已开源
• 学习与生活-专栏：可以了解博主的学习历程
• 算法专栏：算法收录

更多博客与资料可查看👇🏻获取联系方式👇🏻，🍅文末获取开发资源及更多资源博客获取🍅

---

整理者：长路 整理时间：2024.1.22