GPU连通域分析方法
第1章连通域分析方法
连通域分析方法用于提取图像中相似属性的区域,并给出区域的面积,位置等特征信息。分为两种,基于游程(Runlength),和基于标记(Label)。
基于游程的方法,按照行对图像进行游程编码,然后,进行深度优先的逐区域扫描,或者广度优先逐行扫描的游程连接。一般来说广度优先扫描只需要扫描一遍游程即得到区域信息,效率较深度优先高。
基于标记的方法,使用一张标记图,将原始图中相似属性的区域,在标记图中赋值为相同的像素。再对标记图进行后处理,得到区域信息。
经过测试,基于游程的方案,不管是传输原始blob图到CPU进行游程提取与连接,还是在GPU中对blob图提取游程(压缩),只拷贝(压缩后)游程信息到CPU,其耗时都比较高。
在3060显卡上,只有当游程像素不超过全图的0.5%的情况下,才会比拷贝全图的方案有优势。在3090显卡上,只有当游程像素不超过全图的1.5%的情况下,才会比拷贝全图的方案有优势。
因此调研了在GPU上进行连通域分析的方法,认为基于标记的方法更适合在GPU上运行,在GPU上直接得到Blob缺陷信息。
基于标记的Komura方法,当前未优化代码,8k8k图像的区域标记在Nvidia的RTX4080上,仅需要3ms,Playne方法仅需要2.4ms。标记压缩耗时当前可以优化到11ms,区域信息提取并拷贝到CPU,需要1ms。相当于15ms内就完成了8k8k图像的blob分析。而基于游程的方法,仅从GPU拷贝8k8k图像的理论耗时就耗时7ms(64M/(12.8G/s70%)),即使采用GPU游程压缩方法,游程压缩步骤耗时也在7ms。
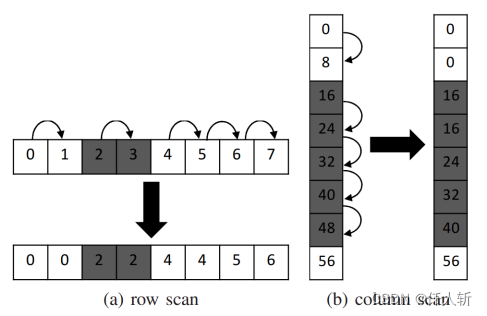
1.1.基于游程的方法
首先对图像按行进行游程编码,然后进行游程连接。
1.1.1.游程编码
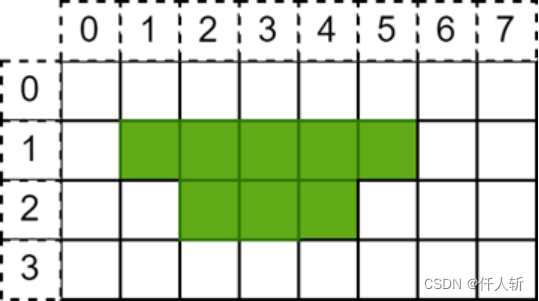
描述方法为:(x1,x2,y),x采用左闭右开区间。(1,6,1),(2,5,2)。采用2个三元组即描述了如上的区域。
该算法逐个读取像素,和阈值进行比较,实际执行效率极其低下。以下为采用SIMD并行指令集优化后的代码片段。
核心的指令共四条:alignr,xor,cmp1,cmp2。
mres = _mm_loadu_si128((const __m128i*)(pBlob1-16))//0-15
m1 = _mm_loadu_si128((const __m128i*)pBlob1); //16-31
mOffset = _mm_alignr_epi8(m1, mres, 1); //1-16
//mH, mL 作差, 一个非0,一个是0,则对应位置赋值为1
mR = _mm_xor_si128(_mm_cmpeq_epi8(mres, mzero), _mm_cmpeq_epi8(mOffset, mzero));
auto a = _pext_u64(_pos, mR.m128i_u64[0]);
while ((uint8_t)a) { pRun1[++n1Count] = x * 16 + uint8_t(a); a = a >> 8; }
auto b = _pext_u64(_pos, mR.m128i_u64[1]);
while ((uint8_t)b) { pRun1[++n1Count] = x * 16 + 8 + uint8_t(b); b = b >> 8; }
alignr实现像素的错位,根据0-15和16-31,生成1-16。
0-15和阈值比较,得到二值,1-16和阈值比较,得到二值。
0-15的二值和1-16的二值异或 xor,结果为1的像素必定为游程的边界。
使用_pext_u64搜集1的位置,得到游程编码。
1.1.2.游程连接
深度优先的方法实现检测,代码容易理解。而广度优先的方法,为了得到极致的效率,采用链表,其数据结构设计通常很复杂。
采用分块的方式,每块放8个游程,块间用链表连接,放满后放到下一个块。
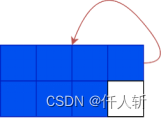
当一个blob有7个游程时:
当一个blob有10个游程时:
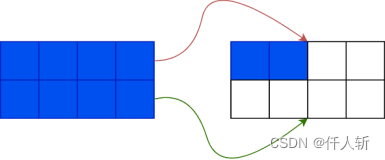
红色的是索引指针,永远指向链表的尾部。绿色是next指针。
当一个blob有18个游程时:
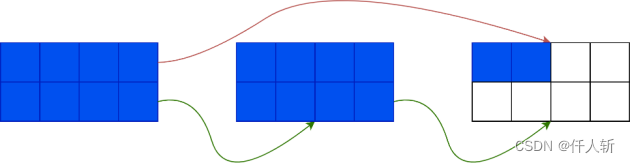
红色的是索引指针,永远指向链表的尾部。绿色是next指针。
可以看到,除了正常的单向链表连接外,设计了从首块到尾块的连接,使用首块的地址作为blob的唯一标识,如果判断新的游程需要加入这个blob,则从首块直接定位到可以加入未满的块。
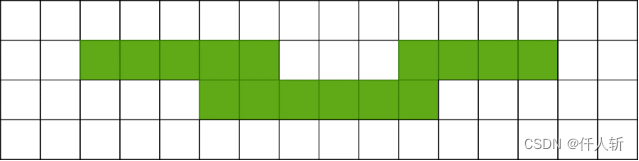
如上图所示,如果两个游程被下面的一行连接到一起,则需要对两个独立的链表进行连接,连接方法为:
当一个有18个游程和一个有20个游程的blob被连到一起后:
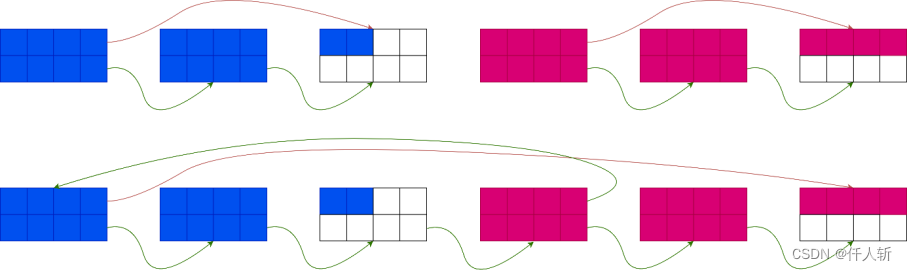
蓝色为B,红色为A。
将B的尾(B的头索引指针指向位置)的next指针指向A的头。
将B的头的索引指针指向A的尾(A的头索引指针指向位置)(新的游程将插入这个分块)。
1.1.3.执行结果
算法执行结果如下:




1.1.4.总结:基于游程的方法是适合CPU的方法
基于游程的方法,不管是游程提取还是游程连接,都适合在CPU完成。
比如游程提取步骤,换到GPU上,每行开启一个线程进行游程提取,其耗时已经超过了从GPU拷贝整张blob图像到CPU的时间。
至于游程连接步骤,则更是不可能在GPU上实现。
1.2.基于标记的方法
首先进行像素标记,然后对标记进行处理得到区域信息。
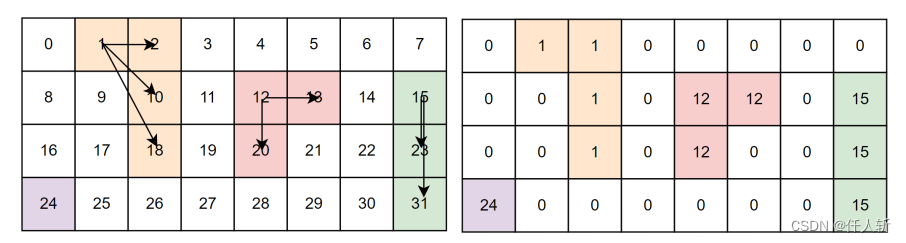
1.2.1.像素标记
将灰度值接近,或者同类像素的对应位置的标记像素设置为相同值。在CPU上采用递归实现。
// 深度优先搜索函数,用于连通域分析和像素标记
void DFS(uint8_t* image, int* labels, int currentLabel, int x, int y, int nW, int nH)
{
if (x < 0 || x >= nW || y < 0 || y >= nH || labels[y * nW + x] != 0 || image[y * nW + x] == 0) return; // 递归终止条件
// 标记当前像素
labels[y * nW + x] = currentLabel;
// 遍历相邻的像素
for (int i = -1; i <= 1; ++i)
for (int j = -1; j <= 1; ++j)
dfs(image, labels, currentLabel, x + i, y + j, nW, nH);
}
// 像素标记
void Labeling(uint8_t* image, int* labels, int nW, int nH)
{
int currentLabel = 0;
for (int i = 0; i < nH; ++i)
{
for (int j = 0; j < nW; ++j)
{
if (image[i * nW + j] == 1 && labels[i * nW + j] == 0)
{
// 新的连通域开始,递增标签值
currentLabel++;
DFS(image, labels, currentLabel, j, i, nW, nH);
}
}
}
}
1.2.2.标记压缩(可选)
在GPU上进行区域信息获取时,需要知道共有多少个区域,或者哪些像素属于同一个区域,在计算特征时,属于一个区域的一堆像素只需要计算一个。
如果在标记阶段,采用深度优先的方法,则标记本身就是连续的,不需要该步骤。
但在GPU的像素标记实现算法中,通常采用合并的方式。因此,标记值必定不是从0到区域数量之间连续的,标记值最大可能是图像的像素个数。
此时需要对标记进行压缩,示意如下:
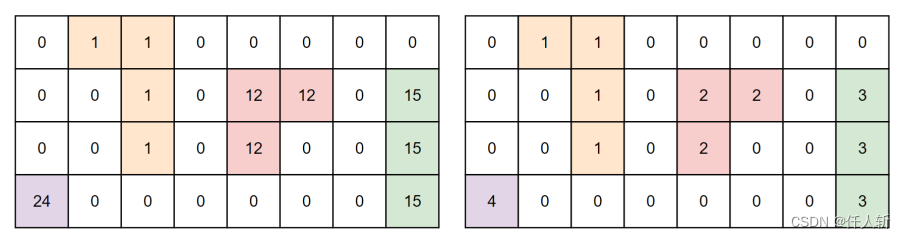
将之前不连续的前景标记修改为1的等差数列,在CPU上实现如下。
void compressLabels(int* labels, int width, int height)
{
std::vector<int> uniqueLabels;
std::unordered_map<int, int> labelMap;
// 1. 找到所有不同的标签值
for (int i = 0; i < width * height; ++i)
{
int label = labels[i];
if (label > 0 && std::find(uniqueLabels.begin(), uniqueLabels.end(), label) == uniqueLabels.end())
{
uniqueLabels.push_back(label);
}
}
// 2. 为每个不同的标签值分配一个新的连续的整数值
int newLabel = 0;
for (int label : uniqueLabels)
{
labelMap[label] = newLabel++;
}
// 3. 遍历标签图,将每个像素的标签值替换为其新的整数值
for (int i = 0; i < width * height; ++i)
{
int label = labels[i];
if (label > 0) {
labels[i] = labelMap[label];
}
}
}
1.2.3.区域信息提取
遍历图像,根据标记值,累加更新对应区域的面积,最大最小更新上下左右4个边界。
std::vector<int> labelAreas(labelCount, 0);
std::vector<int> labelTop(labelCount, nH);
std::vector<int> labelLeft(labelCount, nW);
std::vector<int> labelBottom(labelCount, 0);
std::vector<int> labelRight(labelCount, 0);
for (int i = 0; i < nH; ++i)
{
for (int j = 0; j < nW; ++j)
{
int label = labels[i * nW + j];
if (label > 0) {
labelAreas[label]++;
labelTop[label] = std::min(labelTop[label], i);
labelLeft[label] = std::min(labelLeft[label], j);
labelBottom[label] = std::max(labelBottom[label], i);
labelRight[label] = std::max(labelRight[label], j);
}
}
}
第2章基于标记的方法在GPU实现
1.2节中对基于标记的方式在CPU上的实现进行了原理验证。在GPU上的实现,需要采用不同的算法思路。
2.1.像素标记方法
为了充分利用GPU的并行处理优势,每像素一个线程,进行像素标记。
2.1.1.方案1:Union-Find 方法,2017年提出,Npp使用的方案
实现原理:An Optimized Union-Find Algorithm for Connected Components Labeling Using GPUs (2017)。
Step1:划分为3232的网格,对应1个block最多1024线程。
Step2:每个网格中标记初始化。
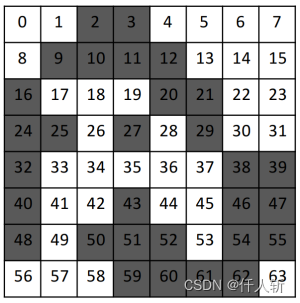
Step3:每个网格进行行列粗合并。
Step3:每个网格局部找根节点并修改标记为根节点标记值。
Step4:所有网格边界像素分析。

直接调用Nppi接口:
status = nppiLabelMarkersUF_8u32u_C1R(
(Npp8u)imSrc.Ptr(), imSrc.Width(),
(Npp32u*)imAResult.Ptr(), imAResult.Width() * imAResult.Depth(),
oSrcSizeROI, nppiNormInf, d_tmp);
对于8k8k大小的图像,RTX4080耗时17ms。
和论文中耗时还有差距(4k4k 1070耗时3.3ms)。
调用Npp,4080显卡,8k*8k图像需要17ms。自己实现可以超过Npp速度。
2.1.2.方案2:Komura方法,2015年提出
Komura亮点:在标记初始化阶段,进行了连接判断。得到一个区域内部像素串。根据像素串找根节点,将所有像素赋值为根节点的标记。
实现原理:GPU-based cluster-labeling algorithm without the use of conventional iteration use of conventional iteration(Komura,小村,2015)
Step1初始化:标记初始化,每个像素如果和左上有连接,初始化为左上像素的标记值。
Step2分析:每个像素找左上,递归找,直到找到根节点,称为root,当前像素赋值为根节点。
Step3合并:标记合并,一个区域多个root的情况消除。
Step4分析:同Step2,重新找根节点。
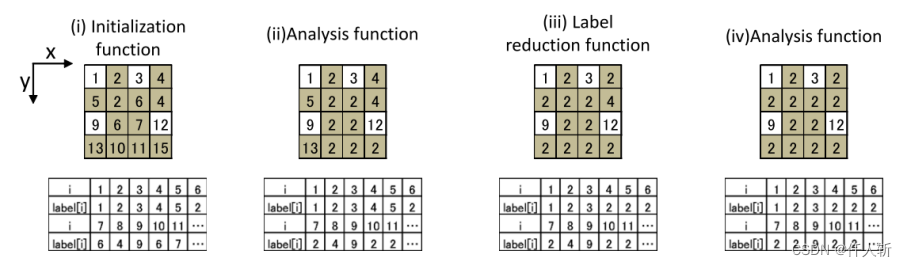
Step5:背景像素标记赋值为0。
该论文中的直接法,有github实现
Github地址:https://github.com/FolkeV/CUDA_CCL
对于8k*8k大小的图像,4080显卡,耗时3.5ms。
论文中给出了Komura直接法和两阶段法的耗时对比

采用两阶段方法,相比直接法,有10%的效率提升。
2.1.3.方案3:Playne方法,2018年提出
实现原理:A New Algorithm for Parallel Connected-Component Labelling on GPUs(Playne 普莱恩 2018)。
论文中对比了label方法,Komura方法和作者本人提出的Playne方法。
Komura方法和Playne方法比较:
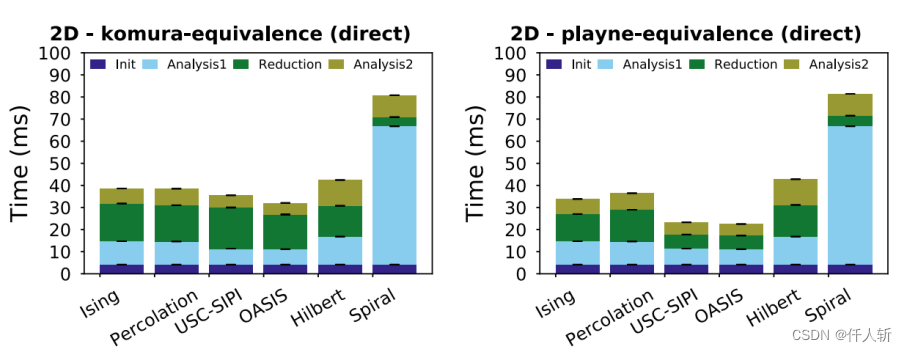
Playne使用两阶段,block,共享内存和shl指令优化。
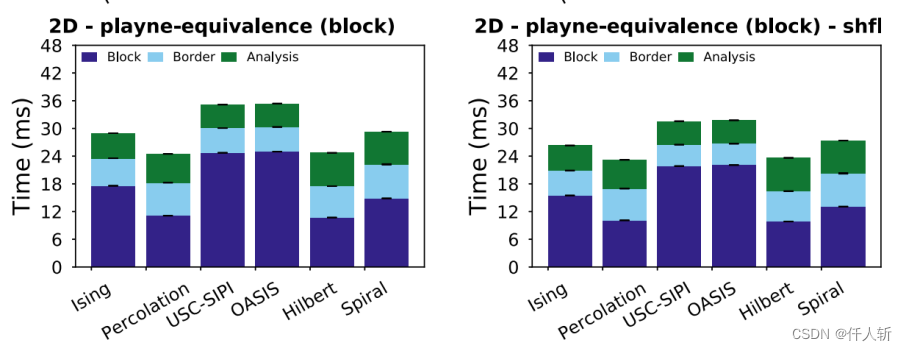
对于Ising数据集,,Playne方法相比Komura有66%的效率提升(40ms->24ms)。
作者使用显卡为K20X,处理能力为3060的1/4,为3090的1/8。即对于8k*8k的图像,完成区域标记仅需要3ms。
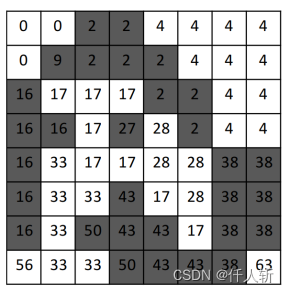
2.2.标记压缩方法
将之前不连续的前景标记修改为1的等差数列,如下图所示:
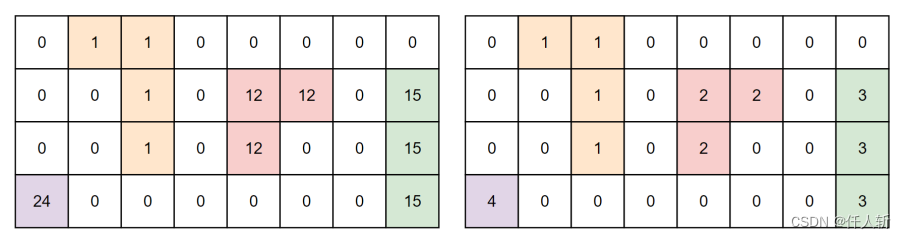
2.2.1.方案1:串行得到压缩后映射关系,耗时6000ms
GPU串行方案,使用1个线程计算压缩前标记和压缩后标记的映射关系,使用像素个数线程修改标记。
1个线程的核函数,8k*8k大小的图像,运行需要6200ms。
__global__ void compressLabelsGetMax(int* labels, int* labelMap, int* nCount,int width, int height)
{
bool isFind;
for (int i = 0; i < width * height; ++i)
{
int label = labels[i];
if (label <= 0)
continue;
isFind = false;
for (int j = 0; j < *nCount; j++)
{
if (labelMap[j] == label)
{
isFind = true;
break;
}
}
if (!isFind)
{
labelMap[(*nCount)++] = label;
}
}
}
而得到映射关系后,使用像素个数线程修改标记的核函数,运行时间为4ms,核函数实现在第2章2.3小节。
2.2.2.方案2:排序+去重,当前最优实现12ms
拷贝图像,所有像素排序,去掉相邻的重复像素。
//图像拷贝0.9ms
cudaMemcpy(d_labels_cpy, d_labels, numPixels * sizeof(int), cudaMemcpyDeviceToDevice);
//数据结构转换
device_ptr<uint32_t> dev_ptr(d_labels_cpy);
device_vector<uint32_t> d_vector(dev_ptr, dev_ptr + nW * nH);
//GPU排序10ms
GPU_sort(d_vector.begin(), d_vector.end());
//相邻的重复像素去重 0.6ms
auto uni = GPU_unique(d_vector.begin(), d_vector.end());
//blob数量
nCompressedLabelCount = uni - d_vector.begin();
std::cout << nCompressedLabelCount << std::endl;
拷贝图像0.9ms,像素排序10ms,去掉相邻的重复像素0.6ms,共耗时11.5ms。
逐像素映射的核函数耗时0.5ms,共耗时12ms。
该方法在stackoverflow也查到过:
https://stackoverflow.com/questions/28797147/compress-sparse-data-with-cuda-ccl-connected-component-labeling-reduction

另外提供了一种使用thrust::lower_bound代替二分查找的方案。
二分查找的方案:
https://stackoverflow.com/questions/21658518/search-an-ordered-array-in-a-cuda-kernel
2.2.3.方案3:直接调用Nppi提供的接口
nppi中提供的接口,对标记图进行原地操作,直接得到压缩后的图像;
status = nppiCompressMarkerLabelsUF_32u_C1IR((Npp32u*)d_labels, numCols * 4, oSrcSizeROI,
nW * nH, &nCompressedLabelCount, d_tmp2); //12ms
总耗时12ms,和方案2耗时接近。因此猜测nppi中原理同方案2。
2.3.标记映射方法
根据2.2.1和2.2.2中得到的映射表,修改标记图像素。核函数实现,对于8k*8k大小的图像,运行需要4ms:
__global__ void compressLabelsRemap(int* labels, int* labelMap, int* nCount, int width, int height)
{
int x = blockIdx.x * blockDim.x + threadIdx.x;
int y = blockIdx.y * blockDim.y + threadIdx.y;
int i = 0;
if (x < width && y < height)
{
int index = y * width + x;
int label = labels[index];
bool isFind = false;
for (i = 0; i < *nCount; i++)
{
if (label == labelMap[i])
{
isFind = true;
break;
}
}
if (!isFind)
return;
labels[index] = i;
}
}
需要对于8k*8k大小的图像,需要4ms。
https://stackoverflow.com/questions/21658518/search-an-ordered-array-in-a-cuda-kernel
这个可以优化,参考这个链接,使用二分搜索,有6倍的效率提升,可做到1ms以下。
2.4.区域信息提取方法
根据1.2.3中CPU上的代码中for循环内容放到核函数,一个线程计算一个像素,最终得到,8k*8k图像,允许耗时0.4ms。
__global__ void compute_blob_info(unsigned int* labels, int* labelAreas, int* labelTop, int* labelLeft, int* labelBottom, int* labelRight, int labelCount, int width, int height)
{
int x = blockIdx.x * blockDim.x + threadIdx.x;
int y = blockIdx.y * blockDim.y + threadIdx.y;
if (x >= width && y >= height)
return;
int label = labels[y * width + x] - 1;
if (label >= labelCount || label <= 0)
return;
atomicAdd(&labelAreas[label], 1);
atomicMin(&labelTop[label], y);
atomicMin(&labelLeft[label], x);
atomicMax(&labelBottom[label], y);
atomicMax(&labelRight[label], x);
}
2.5.存在问题及解决方案
基于标记的方案,暂时可以拿到缺陷的外接矩形和面积。缺陷的对比度,可以在GPU中计算,缺陷的区域,如果支持GPU图像直接显示,也可以在界面展示。
标记图采用Int32 最大支持4k4k的图像。 可以采用分块的形式接触限制。
标记压缩步骤当前还没有找到比较好的优化方案,当前最优实现方案和nppi的耗时相当,8k8k的图像需要12ms。
第3章基于游程的方法在GPU实现
1.2节中对基于标记的方式在CPU上的实现进行了原理验证。在GPU上的实现,需要采用不同的算法思路。
方案1:将blob全图从GPU拷贝到CPU,在CPU中完成游程提取。
方案2:在GPU中完成游程提取,进行压缩后,拷贝到CPU。
如下图所示,对图中的游程区域进行提取并压缩,增加图中游程区域的数据量,进行耗时统计,图像大小为8K*8K,按游程区域占比为1%,2%,4%,100%进行统计。


3.1.游程提取
游程提取完成如下操作:
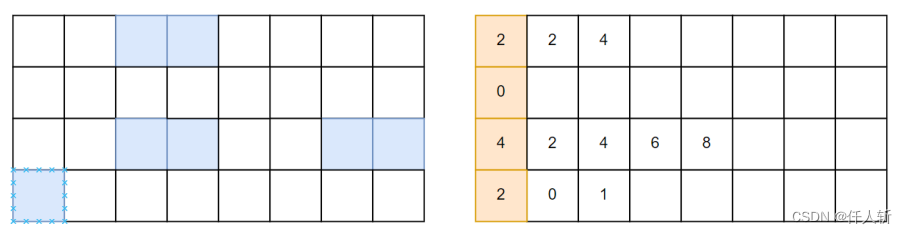
使用一张游程图像,记录每一行前景区域的左右边界。每行开启一个线程,进行游程提取,统计游程的占比对游程提取耗时的影响。在4080显卡上进行测试,图像大小为8K*8K。
| ms | 1% | 2% | 4% | 100% |
|---|---|---|---|---|
| 游程提取 | 1.3 | 1.3 | 1.3 | 0.6 |
不管提多少数据量的游程,耗时无变化。
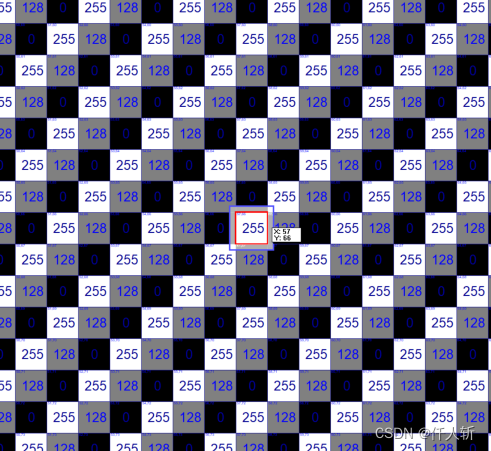
100%游程图像8k*8k,由于有规律所以耗时短。
template<bool bLight>
__global__ void GetRun(uint8_t* d_blob, uint16_t* d_run, int nRunStep, uint32_t* d_count, int nHeight, int nWidth,int nThre)
{
const unsigned int iy = (blockIdx.x * blockDim.x) + threadIdx.x;
if (iy >= nHeight)
return;
uint8_t* pLine = d_blob + iy * nWidth;
uint16_t* pRunLine = d_run + nRunStep / sizeof(uint16_t) * iy;
uint16_t nRun = 1;
uint16_t nRunCount = 0;
bool bFlag = false;
int ix;
for (ix = 0; ix < nWidth; ix++)
{
if (bLight)
{
if (pLine[ix] > nThre)
{
if (!bFlag)
{
pRunLine[nRun++] = ix;
bFlag = true;
}
nRunCount++;
}
else
{
if (bFlag)
{
pRunLine[nRun++] = ix;
bFlag = false;
if (nRun / 2 > 499)
break;
}
}
}
else
{
if (pLine[ix] < nThre)
{
if (!bFlag)
{
pRunLine[nRun++] = ix;
bFlag = true;
}
nRunCount++;
}
else
{
if (bFlag)
{
pRunLine[nRun++] = ix;
bFlag = false;
if (nRun / 2 > 499)
break;
}
}
}
}
if (bFlag)
{
pRunLine[nRun++] = ix;
}
pRunLine[0] = nRun - 1;
d_count[iy] = nRun;
//if (iy == 0)
//{
// for (int i = 0; i < nRun; i++)
// printf("%d ", pRunLine[i]);
// printf("\n");
//}
}
这个实现不一定是最优的,亮暗同时提取,应该能实现更快的速度。
GetRun<true> << <grid, block >> > (d_blob, d_run, nRunStep, d_count, nH, nW, 128+6);
GetRun<false> << <grid, block >> > (d_blob, d_run + nRunStep/sizeof(uint16_t) * nH, nRunStep, d_count, nH, nW, 128 - 6);
提取结果:
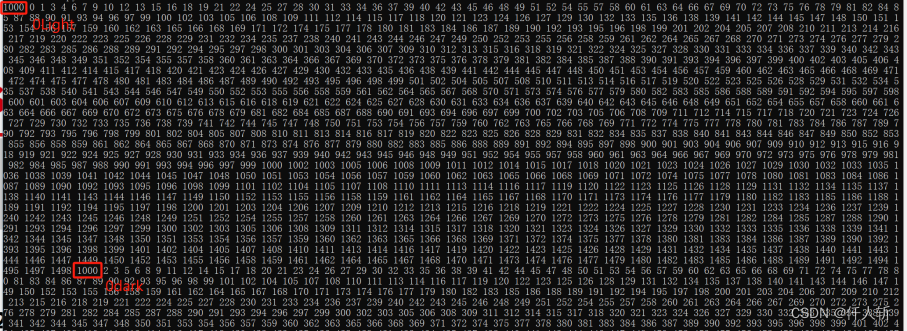
3.2.游程压缩
游程压缩做如下操作:
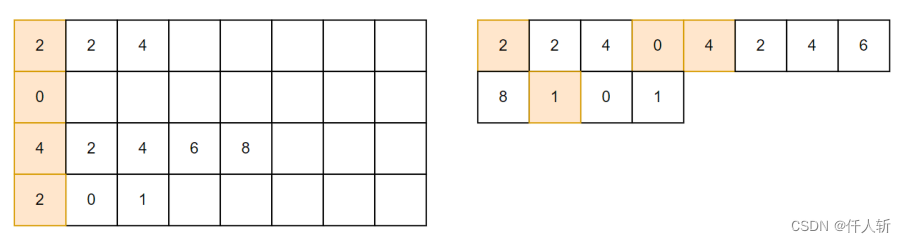
将每一行稀疏的游程,拷贝到一起,便于拷贝传输。为了实现并行拷贝,需要知道每一行存放的起始位置,这个操作就是前缀和。
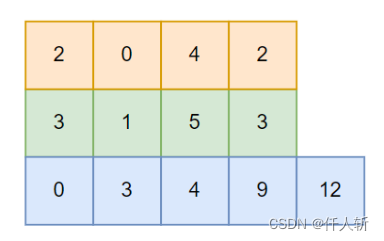
首先计算绿色数组,由于要存放游程个数,因此,每个元素加1。
然后计算蓝色数组,每个元素是绿色数组中下标小于当前下标的所有像素和。
如果采用如下的核函数计算,则不能充分利用CPU的并行计算能力:
__global__ void GetRun(uint32_t* d_count, uint32_t* d_presum, int nLength)
{
const unsigned int ix = (blockIdx.x * blockDim.x) + threadIdx.x;
if (ix >= nLength)
return;
for (int i = 0; i < ix; i++)
d_presum[ix] = d_count[ix];
}
采用GPU前缀和优化方法,当前采用thrust中接口:
thrust::exclusive_scan(thrust::device, d_count, d_count + nHRun, d_presum); //0.04
则耗时可以忽略不计。
然后每行开启一个线程,进行游程数据拷贝,最后一行线程计算压缩后数据长度:
__global__ void copy_height(uint16_t * pRun, int nRunStep, uint32_t * d_count, uint32_t * d_presum, int nHeight, uint16_t * pCompressRun, int* pnCompressLenght)
{
const unsigned int iy = (blockIdx.x * blockDim.x) + threadIdx.x;
if (iy >= nHeight)
return;
memcpy(pCompressRun + d_presum[iy], //To
pRun + nRunStep / sizeof(uint16_t) * iy, //From
(d_count[iy]) * sizeof(uint16_t)); //Count
if (iy == nHeight - 1)
{
*pnCompressLenght = d_presum[iy] + d_count[iy] + 1;
}
}
核函数的调用方法如下:
dim3 block1(16);
dim3 grid1((nHRun + 15) / 16);
copy_height << < grid1, block1 >> > (d_run, nRunStep, d_count, d_presum, nHRun, d_pCompressRun, pnCompressLenght);
在4080显卡上进行测试,图像大小为8K*8K。
| ms | 1% | 2% | 4% | 100% |
|---|---|---|---|---|
| 前缀和计算 | 0.04 | 0.04 | 0.04 | 0.04 |
| 游程压缩 | 0.04 | 0.05 | 0.07 | 0.6 |
| 随着提取游程数量的增加,压缩的耗时也会增加,但总体耗时不超过1ms。 |
3.3.游程拷贝
将压缩后的游程从GPU拷贝到CPU。
对于一张8K*8K的图,3060显卡,GPU拷贝到CPU上耗时8ms,下表统计不同游程数据压缩后的拷贝耗时,相比于blob全图拷贝,有多少提升,单位为ms。
100%前景像素blob图像,每行最多提取500个游程。
| ms | 1% | 2% | 4% | 100% |
|---|---|---|---|---|
| 压缩数据拷贝 | 0.07 | 0.1 | 0.14 | 0.54 |
| 占全图拷贝% | 0.8% | 1.25% | 1.7% | 6% |
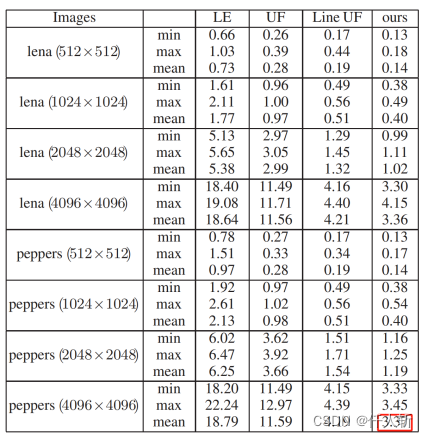
3.4.效率比较
方案1:GPU拷贝完整blob图到CPU,在CPU中完成游程提取。
方案2:GPU进行游程提取,并进行游程压缩,将压缩后游程拷贝到CPU。
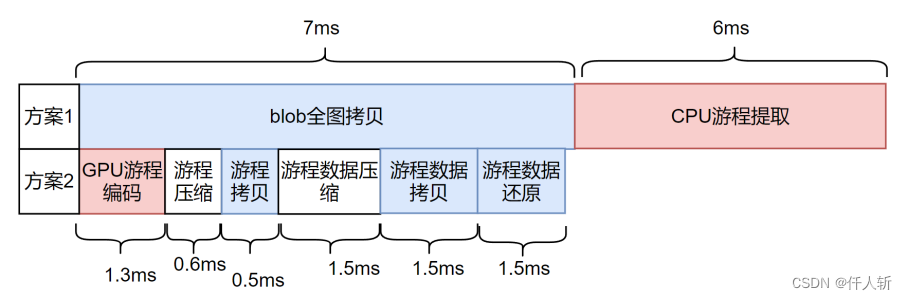
100%游程像素下(每行最多取500个游程)
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【论文阅读】深度学习方法在数字岩石技术中的应用进展
- Vue3新特性defineModel()便捷的双向绑定数据
- vue中导航守卫有哪三种?分别有什么作用
- 设计模式(4)--对象行为(8)--状态
- C语言前置和后置递增或递减操作符
- Elasticsearch 分片滚动查询与数据准确性
- Metapreter 详细教程--进阶教程
- 【精选】计算机网络教程(第6章应用层)
- Node.js+Express 路由配置,实现接口分类管理
- Elasticsearch本地单机配置以及php组件使用记录