【深度学习-基础学习】Self-Attention 自注意力机制 笔记
- 本篇文章学习总结 李宏毅 2021 Spring 课程中关于 Self-Attention 自注意力 机制相关的内容。
- 课程链接以及PPT:李宏毅Spring2021ML
关于 Self-Attention 机制想要解决的问题

- 通常来说, 我们的模型的输入会是一个vector,然后输出可能是 一个数值(Scalar)或者是一个类别(Class)。
- 但是,在机器学习中会碰到输入是 一堆vector,并且这些vector的具体的格数也是不明确的,面对这样的输入,我们的模型需要输入 一堆数值(Scalars)或者一堆类别(Classes)。
对于一堆vector,我们称其为一个Sequence,由多个vector组成。
事实上,我们有这样的任务,输入是一个不知长度的Sequence,这个任务就是文本、语音、图相关的任务。
-
文本任务:
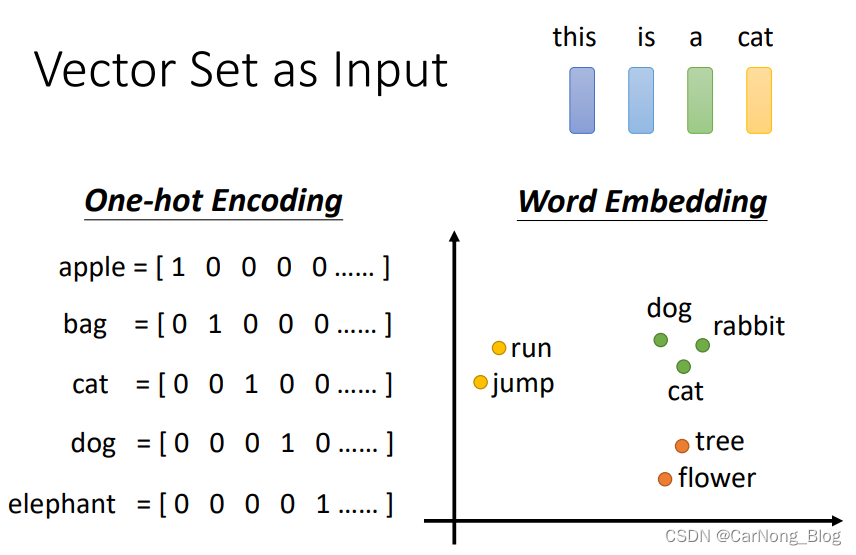
对于文本任务,因为对于每一个单词我们会采用 One-hot Encoding 或者 Word Embedding 的方式对文本进行编码,这个时候一段文本就是一个 vectors 的 Sequence,而这个Sequence的长度是取决于文本的长度。 -
语音任务:
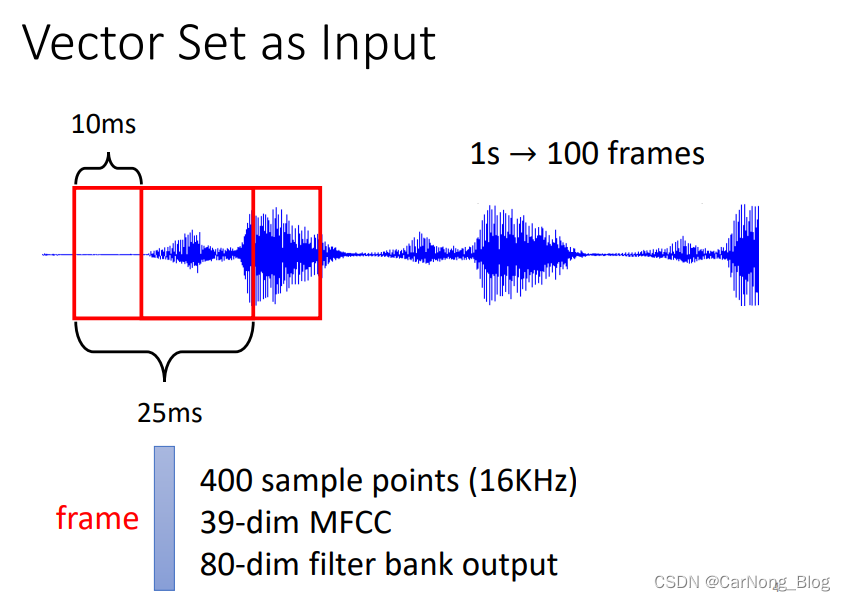
对于一个语音任务,对于每个小的时间段的语音信息,我们会将其编码为一个frame,这个frame也是一个vector,因此,整段语音也会作为一个vector的Sequence作为输入,这个sequence的长度取决于语音的长度。 -
图任务:
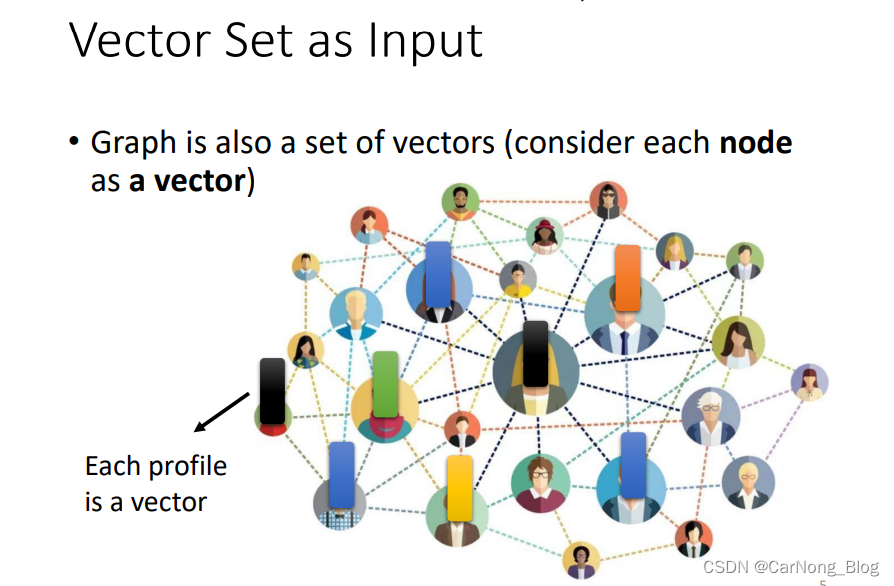
对于图任务,这里以人类的社交图为例子,每个点都是具体的人,而通过编码这个人的个人信息(profile),可以获得一个vector,而整幅图就是一个vector的集合,也就是一个Sequence,这个Sequence的长度则取决于这个图中人的数量。
因此,综上所述,我们直到在机器学习领域中,是存在非常多对于输入是一个不确定长度的、由多个vector组成的 Sequence的任务的,比如文本任务、语音任务、与图有关的任务。
接下来,我们需要讨论的是:关于这些Sequence作为输入的情况,输出有哪些情况呢?
-
- 每个输入vector有一个标签(N-N):
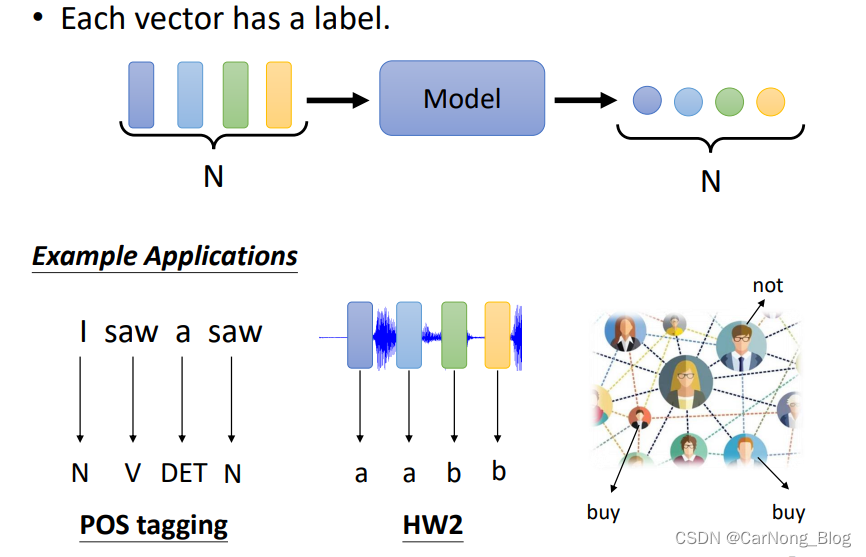
- 每个输入vector有一个标签(N-N):
假设对于文本任务中的词性分析任务,输入是一个文本句子,我们需要将组成句子的单词划分词性:
- I — N词性
- saw — V词性
- a — DET词性
- saw — N词性
此时,每一个vector,也就是每一个单词,都有一个对应的类别(词性),我们按照输入vector的个数,输出对应个数的类别即可。
-
- 整个Sequence具有一个标签(N-1):
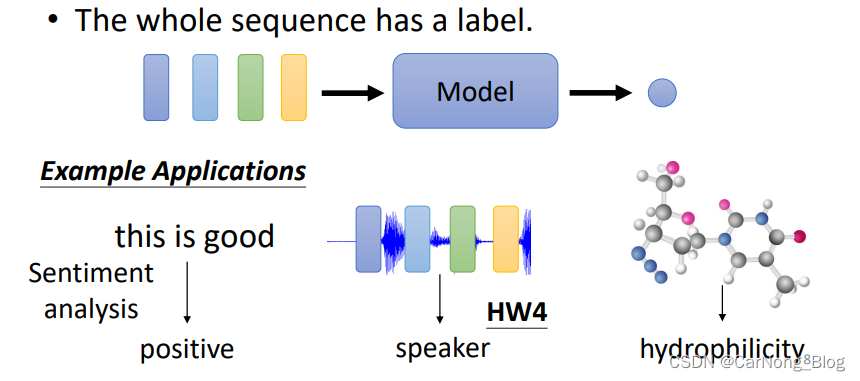
- 整个Sequence具有一个标签(N-1):
假设对于文本任务中情感分析任务,需要对整个句子的情感做出分析,比如是负面情感还是正面情感:
- positive — 整个句子是正面情感
- negative — 整个句子是负面情感
此时,有多个vector组成的sequence,也就是整个句子只有一个标签,因此不管多少个vector,只会产生一个标签。
-
- 由模型决定输出的Sequence的长度(N-M):
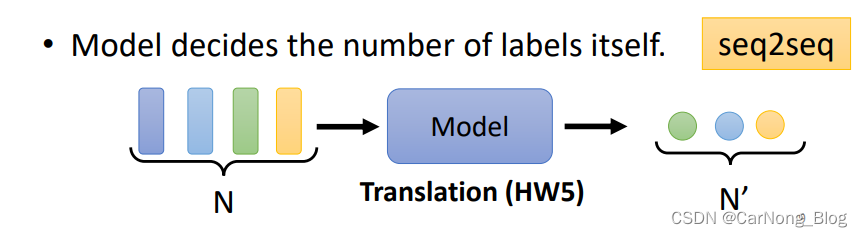
- 由模型决定输出的Sequence的长度(N-M):
举一个简单例子就是,在文本任务中的翻译任务,假设需要将英文翻译成中文,输出的中文句子的长度其实并不是确定的,而是根据输入的英文句子所决定的。
此时,对于一个长度的不确定的 Sequence 的输入来说,将有模型自己决定输出的Sequence的长度。
综上,对于未知长度的Sequence作为输入的机器学习任务,存在3种不同的输出情况:
- 每个vector对应于一个标签,因此输出的Sequence的长度等于输入Sequence的长度,例如 词性分析任务。
- 整个Sequence对应于一个标签,因此不论输入的Sequence的长度为多少,输出Sequence的长度都是1,例如 情感分析任务。
- 对于不同长度Sequence的输入,输出的Sequence长度由模型自己决定,例如 翻译任务。
接下来我们将会详细探讨:第一种情况——每个vector对应于一个标签,因此输出的Sequence的长度等于输入Sequence的长度。
第一种输出情况:词性标注任务的分析
从直觉上出发,词性标注任务会非常容易解决,我们只需要将每个词做分类,通过FC(Fully Connected)使用分类算法,就可以得到句子中每个词的词性,如下图所示:
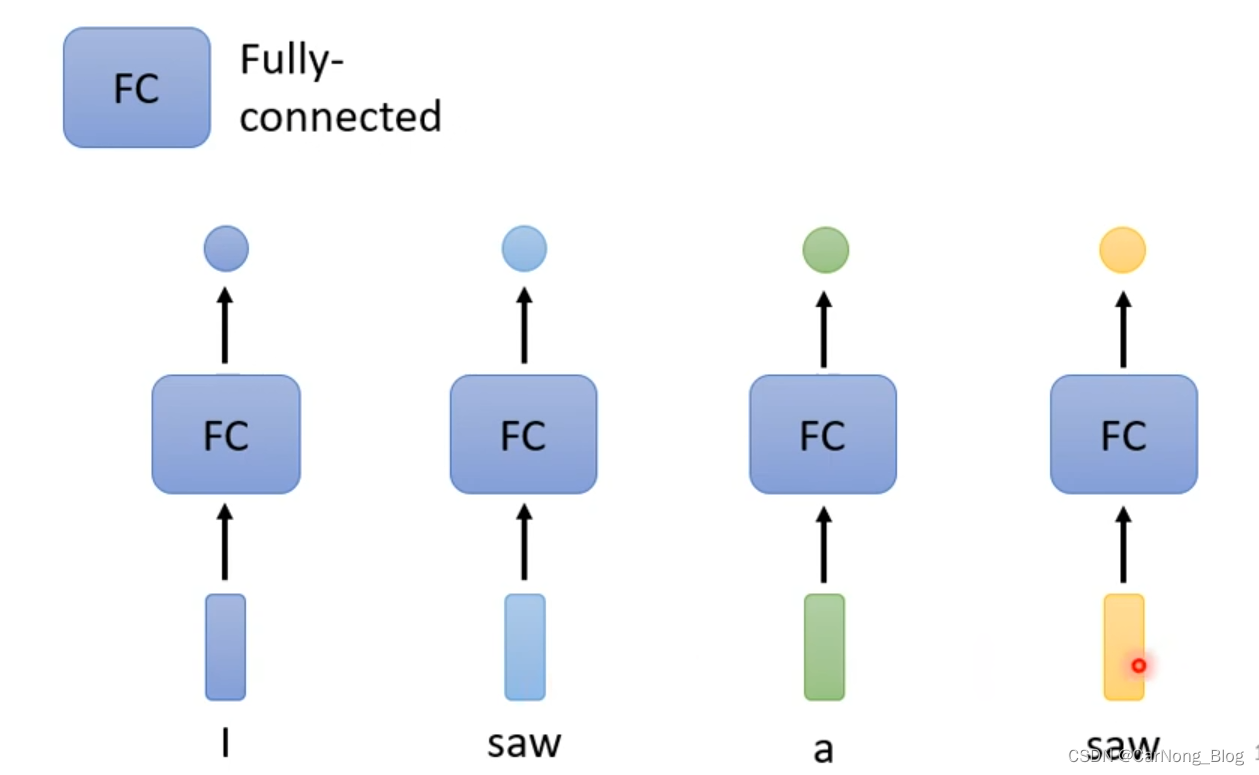
但是,我们会发现存在问题,就是对于 第一个saw和第二个saw来说,它们完全是独立的分类过程,对于模型来说,它们是一模一样的,因此,模型会将它们分类为同一种词性。
这是一个非常大的错误,我们显然直到 第一个saw 是动词,第二个saw 是名词,而当我们使用最简单基于直觉的方法来完成这个句子的词性分析的时候,模型完全不能完成任务。
- 对于以上问题,我们发现,是因为模型并没有考虑上下文的信息,而是将每个词作为独立的分类过程,因此我们需要一种让模型能够考虑上下文的机制。
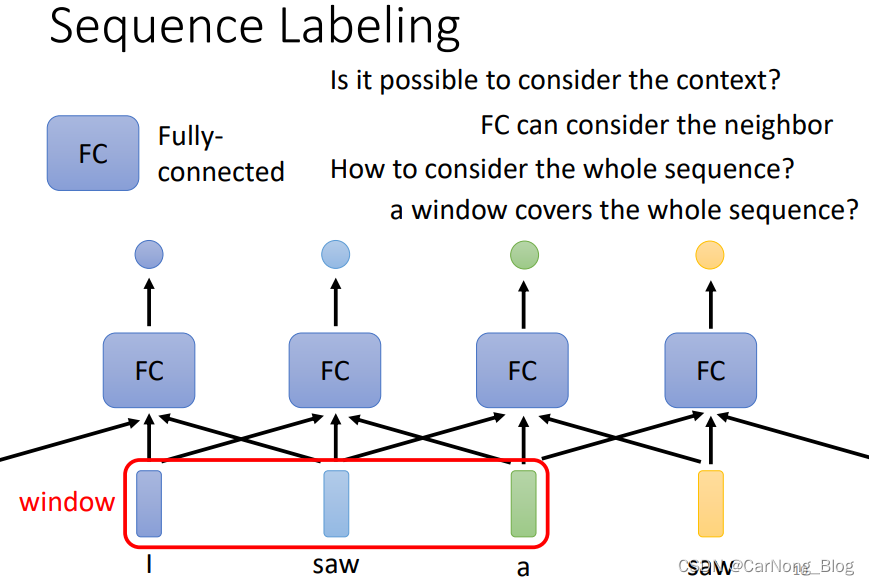
我们非常容易想到上图的方式,在之前模型分类无法考虑到上下文的信息,是因为我们传入FC层的信息只有当前词汇的vector,那我们只需定义一个window,FC接收的vector信息是这个window中所有词汇的vector,这样的话,模型就拥有上下文的信息以便更好的对当前词汇做出词性分析。
通过上述方法,模型确实能够考虑一定范围的上下文信息,但是如果需要获取整个Sequence的上下文信息,我们需要将window开辟到整个Sequence的长度,而整个Sequence的长度的window我们是无法提前定义,它完全取决于输入的Sequence,这又是一个值得思考的问题。
综上,我们总结一下:
-
对于词性标注任务,一种最简单的方式就是对每个词汇做简单的分类,将当前词汇输入FC,得到具体的分类,但是这种方式存在问题,模型无法得知上下文的信息,也就是无法得出当前词汇的准确词性分类。
-
我们对最简单的方式进行改善,我们定义一个window,当对某个词汇进行分类的时候,FC不仅接收关于当前词汇的vector,还会接收位于window窗口中词汇的vector,这样模型就获取到相关的上下文信息,但是这种方式页存在问题,当我们需要获取足够多的上下文信息以至于需要将window开到整个sequence的长度大小,我们事先无法定义window的大小,因为这取决于输入Sequence的大小。
接下来,我们介绍 Self-Attention 机制,它将有助于解决这些问题。
Self-Attention
- 首先我们对于Self-Attention,我们可以将其理解为一个module。
- 它的作用是 获取N个vector,也就是一个Sequence的输入,然后经过Self-Attention module 内部机制的处理,输入N个vector,也就是一个输出Sequence,输出的每个vector中都融合其他所有vector的一些信息,使它成为了一个 Vector With Context,如下图所示
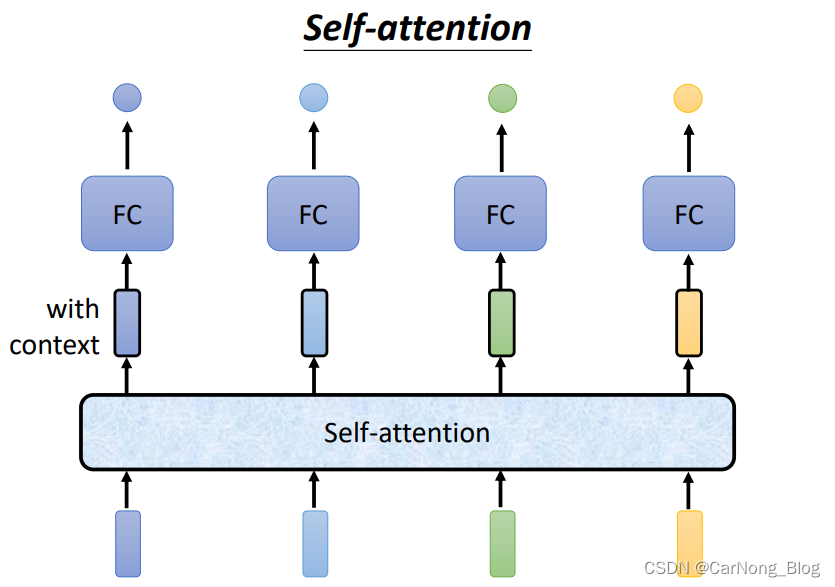
对于Selt-Attention 可以多次重复叠加使用,如下图所示:
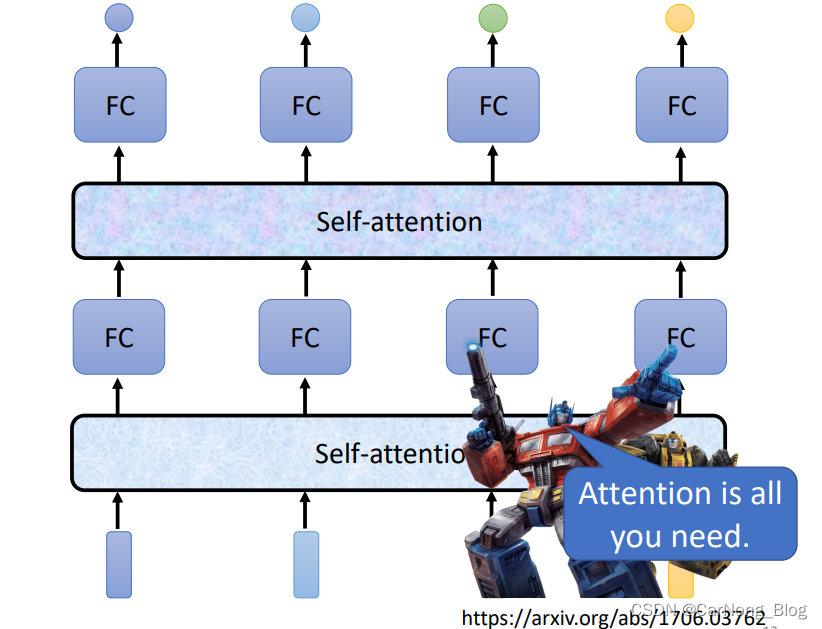
以上就是从整体上了解了Self-Attention,接下来我们将具体了解Self-Attention的细节内容。
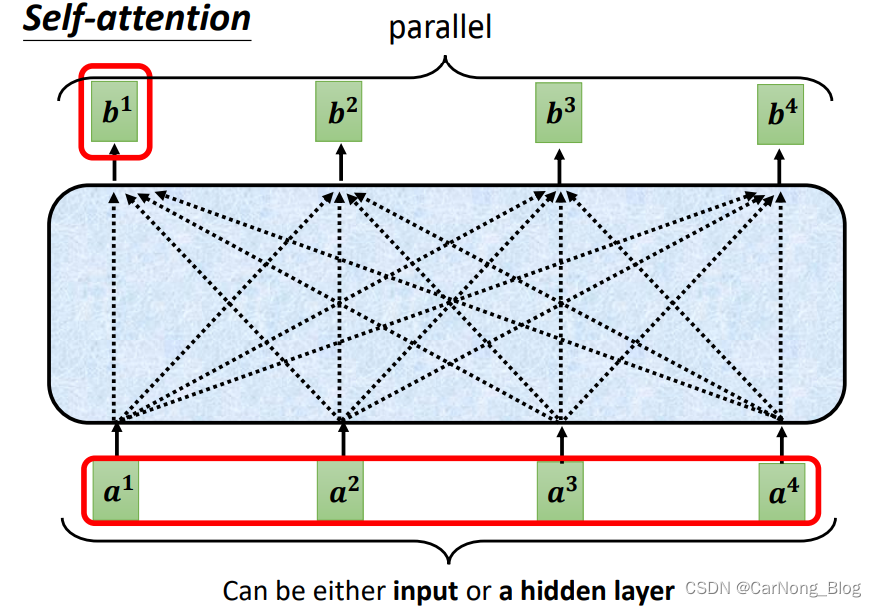
- 首先,Self-Attention 的输入是 N 个 Vetcor,这些 Vector 可以是输入层的输出,也可以是网络中某些 Hidden Layer 层的输出。
- 其次,Self-Attention 的输出是 N 个 Vector,与输出的Vector个数相同,这些Vector是带有整个Sequence上下文信息的Vector(Vector With Context)。
具体如下图所示:
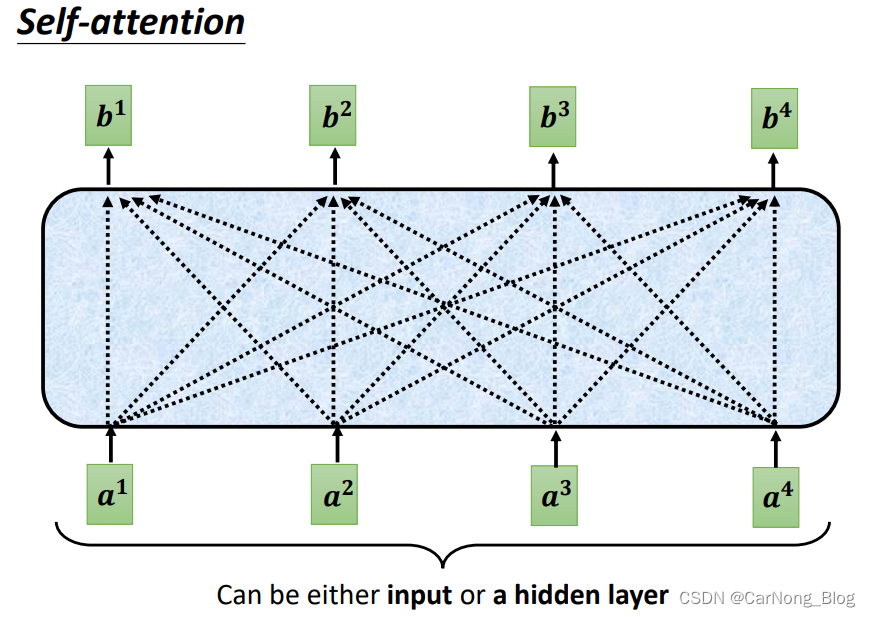
下面我们尝试探究它内部是如何生成Vector With Context的:
对于每个输入Vector,它需要获取其他Vector的信息来组成它的上下文信息,但是,对于不同的vector,可能有些vector的信息更重要,有些vector的信息不那么重要,所以,我们首先需要获得一个相关性的分数,分数越高,代表越重要,在当前Vector中上下文的权重占比也就越高,如下图所示:
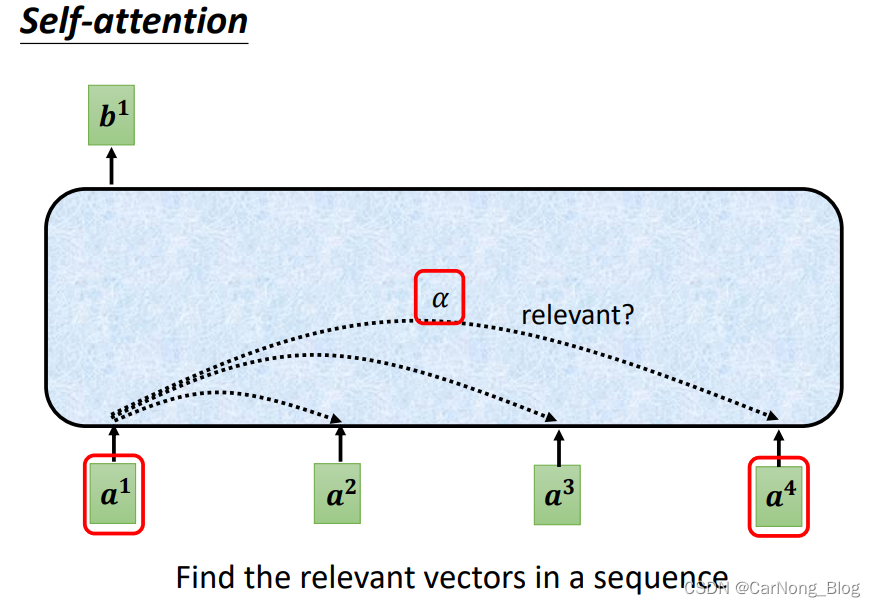
那么,关于这个相关性分数如何计算呢?
一般采用的是 Dot-product 方式,当然也有其他的方式,比如下图右侧的方式,这里主要介绍 Dot-product 的方式,它也是transformer使用的方式:
- 对于当前的Vector,它乘上Wq矩阵,获得一个q向量。(query)
- 对于被关联的Vector,它乘上Wk矩阵,获得一个k向量。(key)
- 然后将 q 和 k 做点积,即可得到相关性分数。
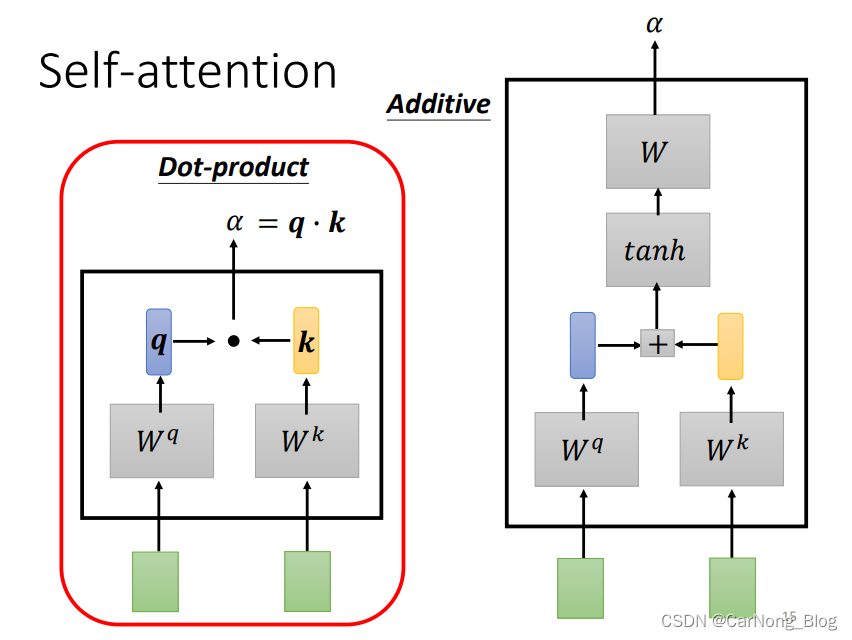
直到了相关性分数的计算方法,下面来看整体的流程。
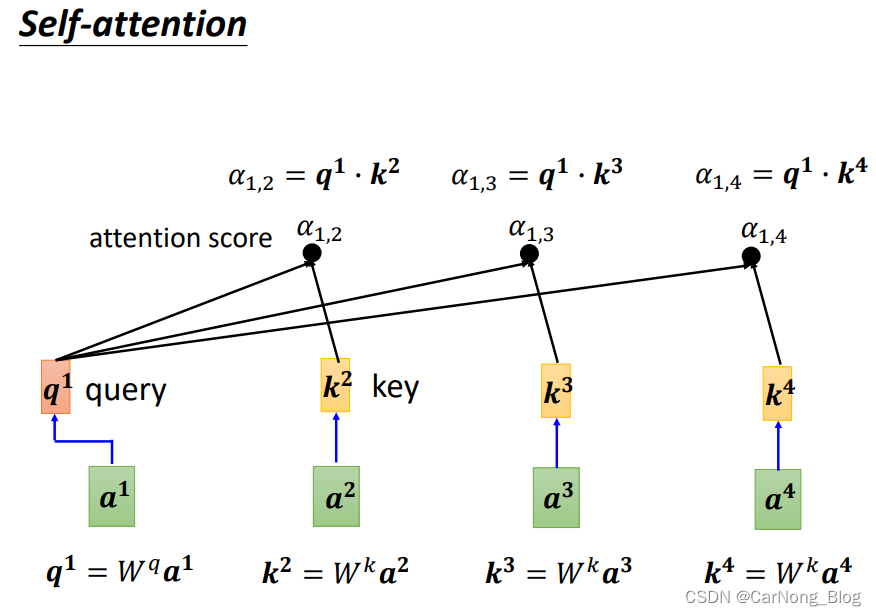
可以这样理解,每个输入的vector,可以通过与Wq,Wk的计算,获得两个vector,分别是 q 和 k。
- q 指的是 query,用于计算当前这个vector和其他vector的Attention Score,也就是相关性分数。
- k 指的是 key,用于被其他vector计算Attention Score,也就是相关性分数。
注意点:每个vector还需要将 自己的 q 和 k 进行内积,计算出自己的Attention Score。
如下图:
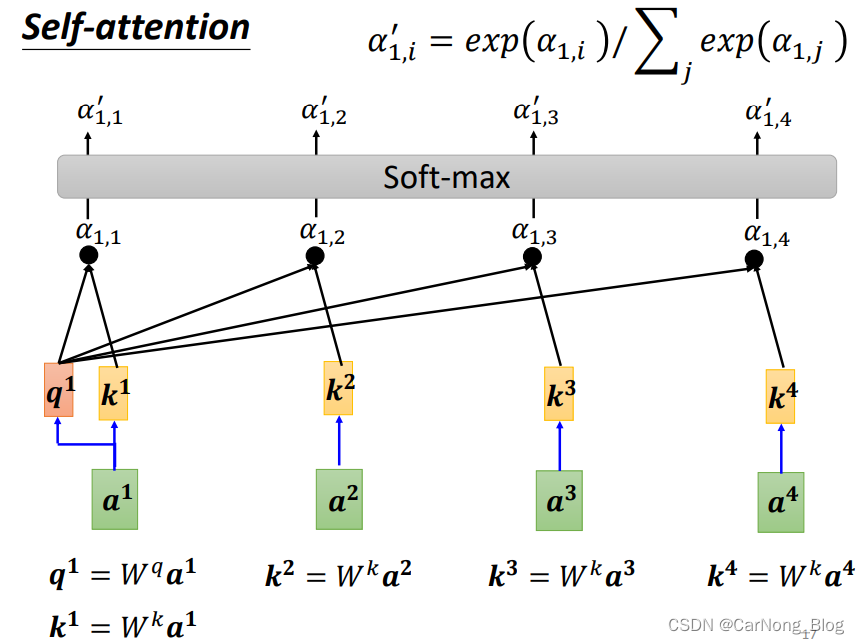
上图由4个vector,对于a1来说,需要计算出4个Attention Score,这并不是最终的结果,还需要经过一层Softmax层,将相关性分数进行处理,使得所有Attention Score之和为1.
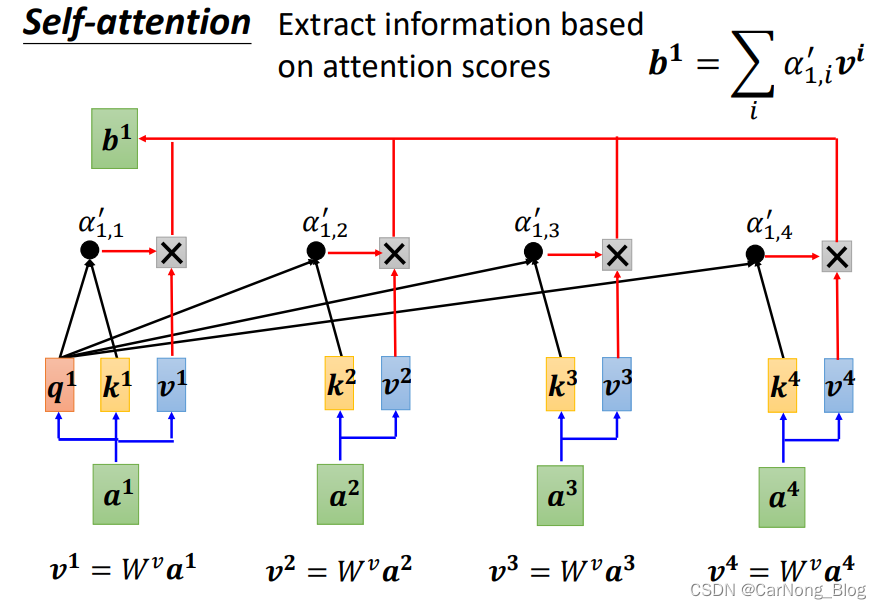
之后,对于每个向量vector,我们不仅仅需要获得其 q 、k 向量,这两个向量仅仅是用来获取Attention Score的,我们还需要获取一个v向量:v = Wv * a,它是用于真正融合上下文信息的向量,我们需要将每个 Attention Score 和 每个向量的v 相乘,以获取最终的输出向量b,如上图所示。
综上所述,我们已经直到了Attention Layer 中的处理方式,我们这里再总结一下:
对于每个输入向量a,我们需要获得其三个向量,分别是q、k、v
- q 向量,q = Wq * a,用于计算当前vector和其他vector的Attention Score。
- k 向量,k = Wk * a,用于被其他vector计算Attention Score。
- v 向量,v = Wv * a,真正包含上下文融合所需信息的vector,它会和Attention Score相乘,输出到最后的输出向量b中。
经过以上的操作,以当前b1输出向量为例,它拥有b2、b3、b4 的上下文信息。
Self-Attention 中 q、k、v 的矩阵运算
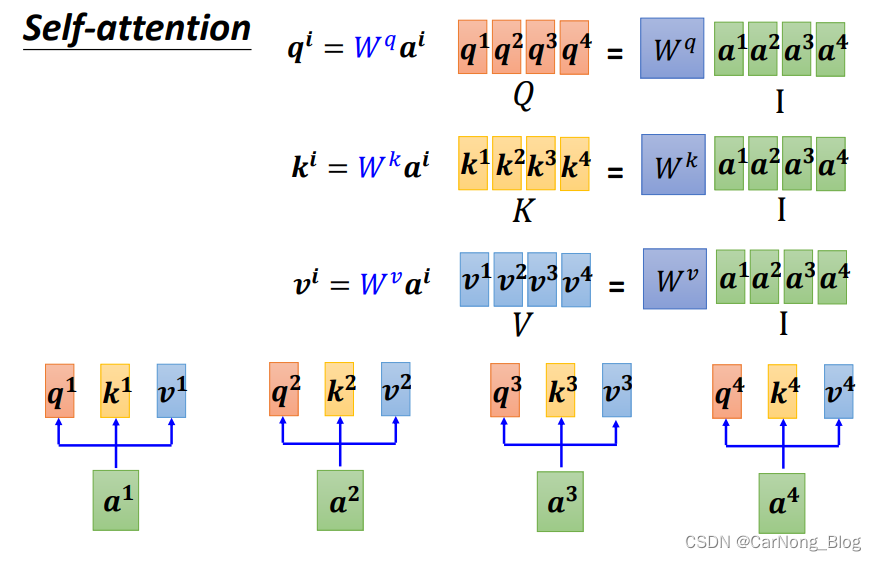
我们之前提到过,每个输入向量a,都需要经过乘 Wq Wk Wv 三个矩阵来获取相关的 q、k、v 向量,这里可以将它们进行矩阵运算以便简化,如上图所示。
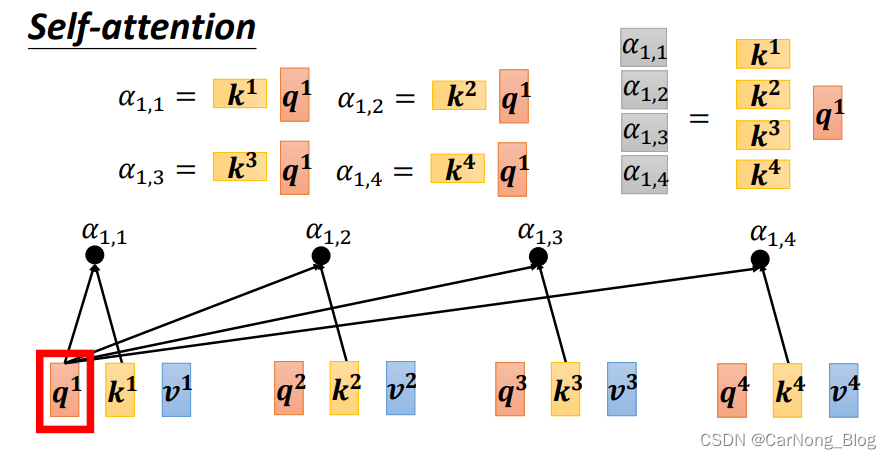
包括 Attention Score 也可以使用类似的矩阵运算来获得,如下图所示。

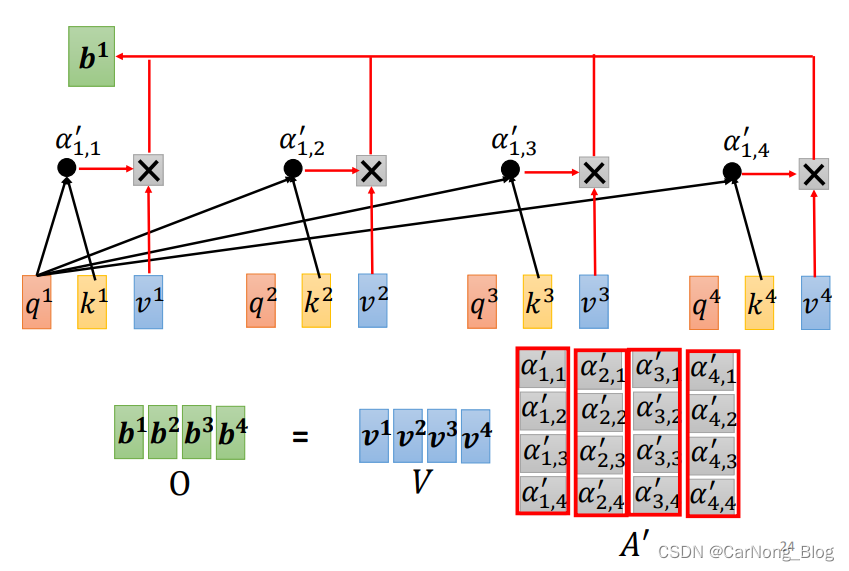
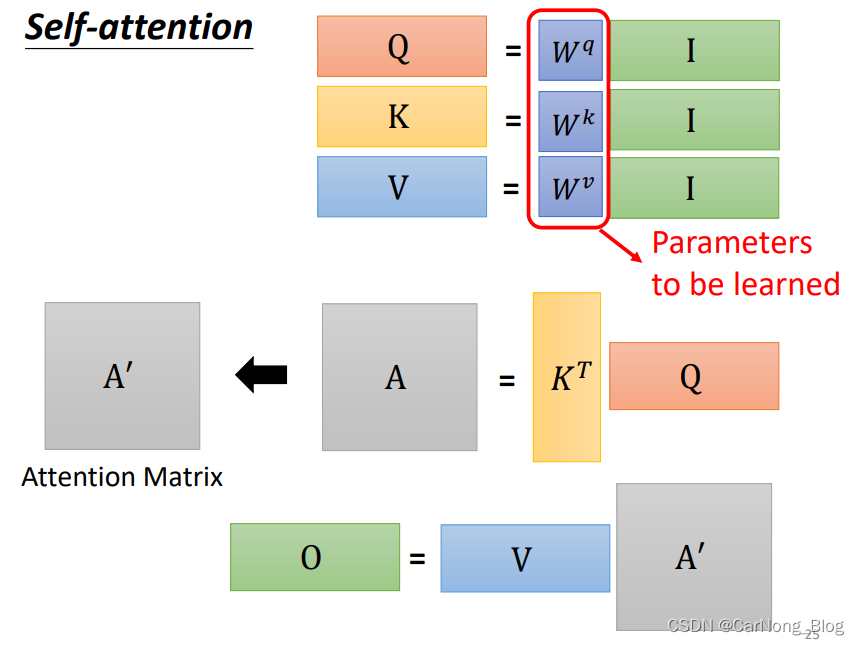
经过整理,我们最终发现,需要通过机器学习自动调整的参数是 Wq 、Wk 、Wv 这三个矩阵中的参数。
Multi-head Self-Attention
Multi-head Self-Attention 主要用于处理 相关性的不同种类。
举个例子,当我们去计算某些vector之间的Attention Score的时候,可能会有 时间意义 上的相关性,可能会有 空间意义 上的相关性,这个时候,说明存在两种不同种类的相关性,我们应该得出两种Attention Score。
实现其实很简单,之前我们计算相关性,每个输入向量a 需要获得一个 q 向量 和一个 k 向量用于计算Attention Score。
这里我们需要计算两个Attention Score,每个输入向量a 需要获得两个 q 向量 和 两个 k 向量用于计算Attention Score,它们代表不同种类的相关性,并且这两个q向量是以原始的q向量所获得。
- qi,1 = Wq,1 * qi
- qi,2 = Wq,2 * qi
而k向量的处理过程也和q向量一样。
如下图所示:
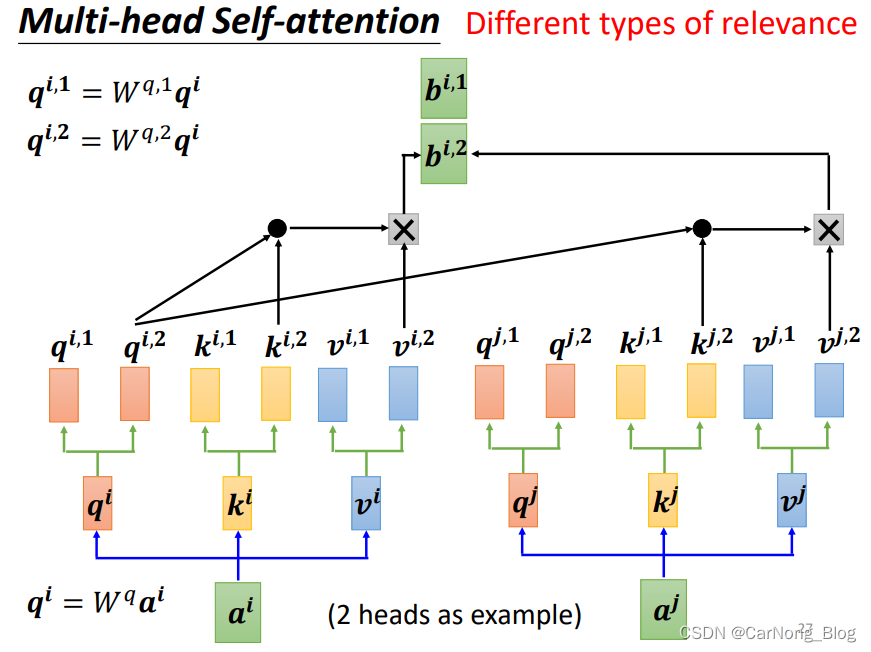
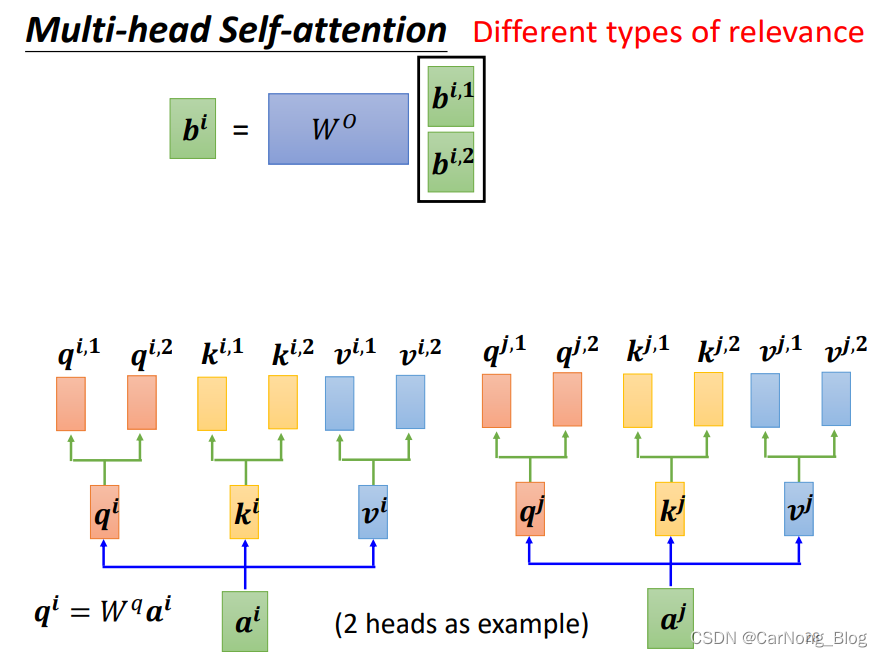
最终,我们需要将 不同种类的Attention Score,乘上不同种类的 v 向量,最终获得多个b向量,我们需要将多个b向量汇聚成一个最终的b向量,通过乘以 Wo 矩阵的方式。
目前 Self-Attention 存在的问题及解决方法
我们现在基本上已经了解 Self-Attention 的概念以及工作方式:它可以融合上下文的信息,以便模型可以参考这些上下文信息计算更精确的输出。
但是我们发现,在融合上下文信息的过程中,我们并没有提供位置信息,比如 b1 是 a1 经过 Attention Layer 的输出,它融合 b2、b3 、b4的信息,但是它并不知道b2、b3、b4的位置信息,它并不知道 b2 是离它最近的,b4 是离它最远的。
所以,我们要引出一个解决方法 Positional Encoding。
Positional Encoding
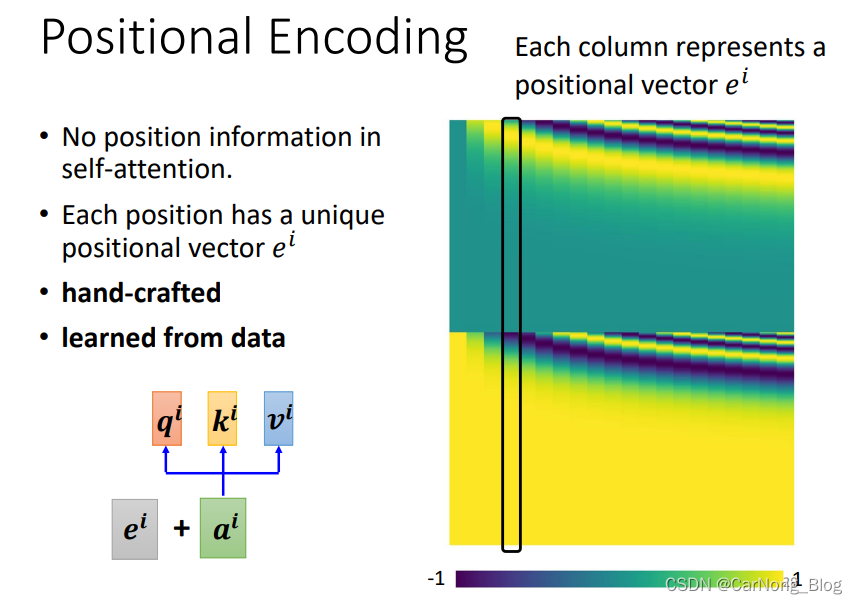
- Self-Attention 机制中没有提供位置的有效信息。
- 每个位置信息可以通过一个vector所表达。
- 可以人工设置。
- 也可以从机器中学习。
我们在输入a向量的同时附加上这个表示位置信息的positinal vector,即可以提供每个vector的位置信息,如上图所示。
总结一下:
Self-Attention 机制中可以帮助融合上下文信息,但是它忽略了位置信息,我们可以通过 Positional Encoding 的技术来传递位置信息,Positional Encoding 有非常多的实现方法,可以是人工设置,也可以是 机器自己学 出来的。
Self-Attention 应用
Self-Attention for NLP
- Self-Attention 在 transfomer 架构中被发扬光大。
- Self-Attention 在 NLP 中的 Bert 中应用广泛。

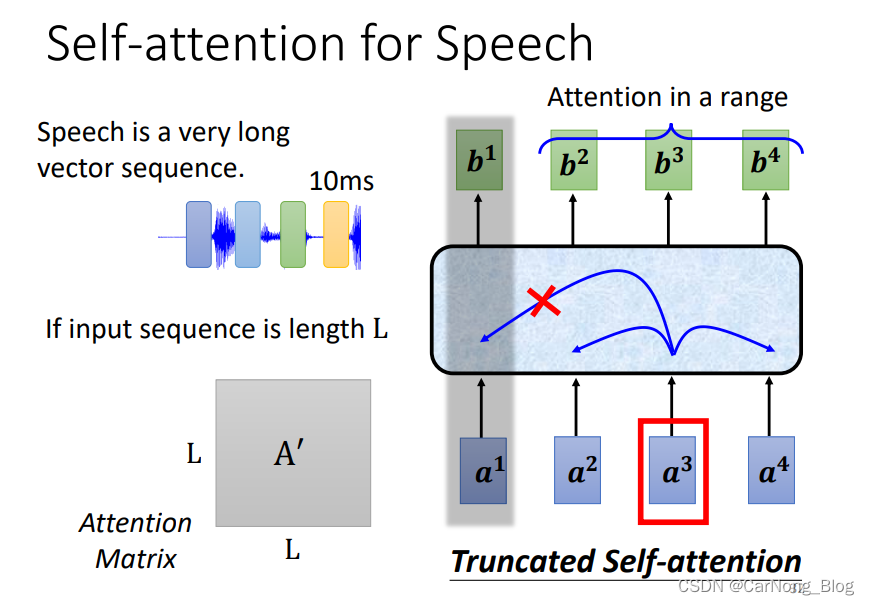
Self-Attention for Speech
在语音领域,Self-Attention 机制也发挥了重要作用。
但是在语音领域,Truncated Self-Attention 更为常用。
因为对于语音来说,可能不需要全局的上下文信息,可能只需要周围几个的上下文信息,即 Attention 是有一个范围的。
Self-Attention for Image
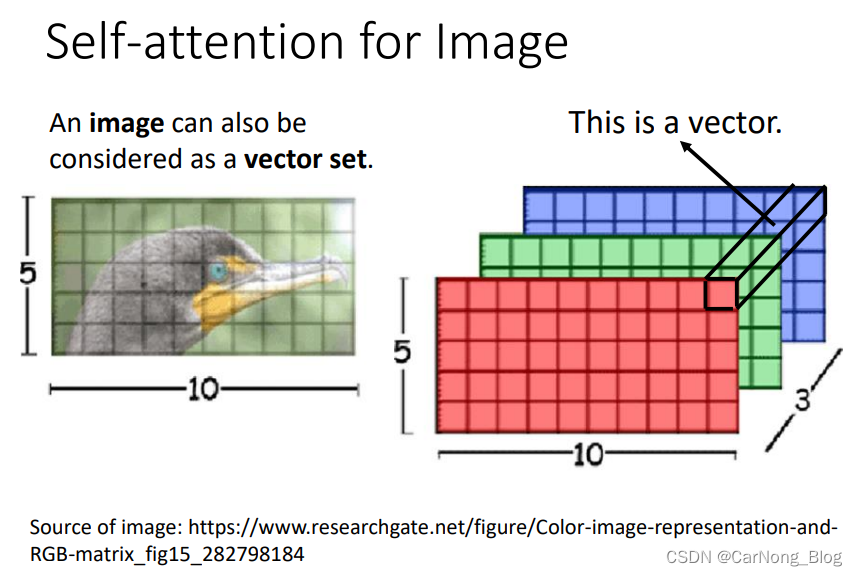
我们可以将每个像素的位置三个通道数视为一个vector,进而使用Self-Attention机制来处理图片。
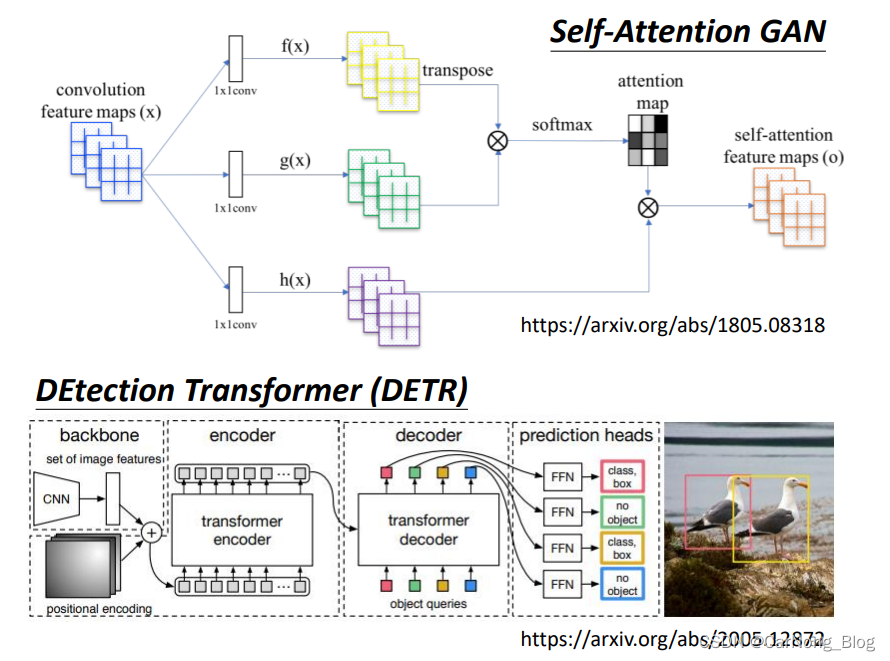
以下是将 Self-Attention 用于图像处理的一些方法
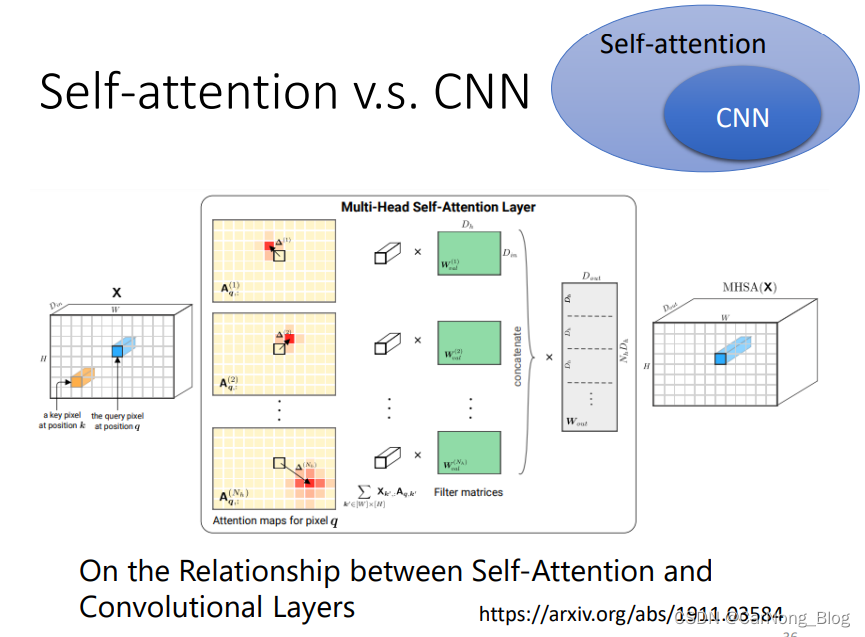
Self-Attention VS CNN

- CNN:可以视为一种只关注 receptive field 范围中上下文信息的 Self-Attention,是一种更简单一些的Self-Attention 机制,且 receptive field 是人为决定的。
- Self-Attention:可以视为一种 receptive field 是自动被机器学出来的CNN,机器自己决定哪些像素和当前像素相关性高,哪些像素和当前像素相关性低,因此,可以将它视为一种更为复杂的CNN。
综上所述:CNN 其实是 Self-Attention 的一种特例,如下图所示
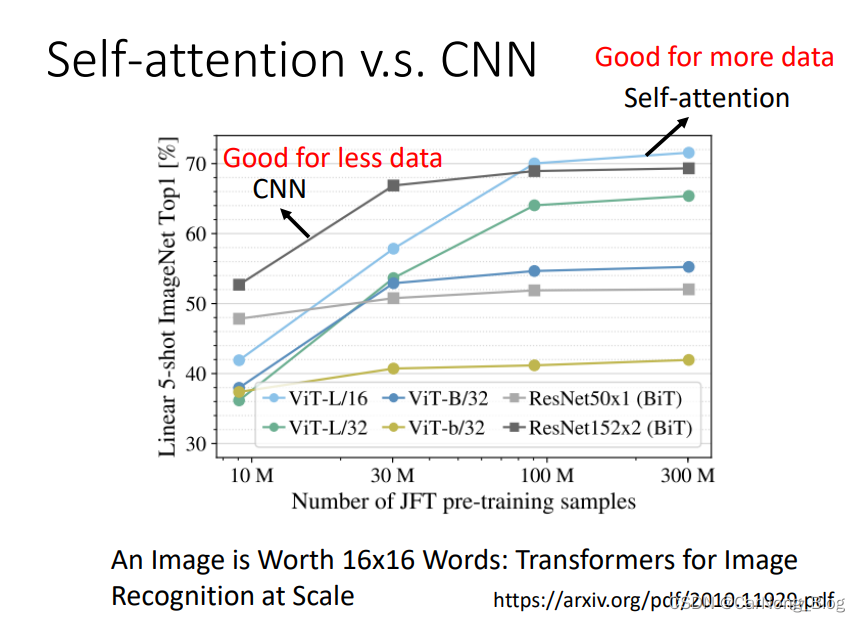
- Self-Attension 是更 flexible 的 CNN,会需要更多的data,对于更少的data,会更容易 overfitting,也就是过拟合。
- CNN 是 更受限制的 Self-Attention,适合在data相对来说更少的时候,不那么容易会 overfitting。
以下是不同data量来训练不同架构(Transformer or CNN)的比较图:
Self-Attention VS RNN
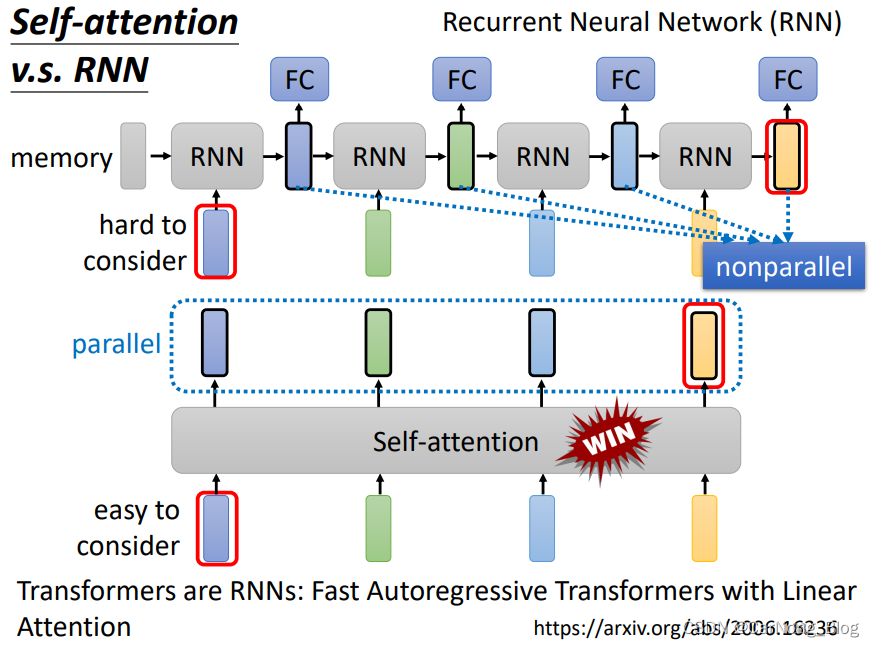
RNN 也可以融合上下文的相关信息,但是对于Self-Attention 来说,它的机制更为繁琐和不那么高效。
首先,单向的RNN只能考虑之前上下文信息,不能考虑全局的上下文或者之后的上下文信息。
如果采用双向的RNN,那么它确实能够达到和Self-Attention 一样的效果,可以考虑 之前、之后的上下文信息,但是它是串行的,Self-Attention是并行的,如下图
Self-Attention for GNN
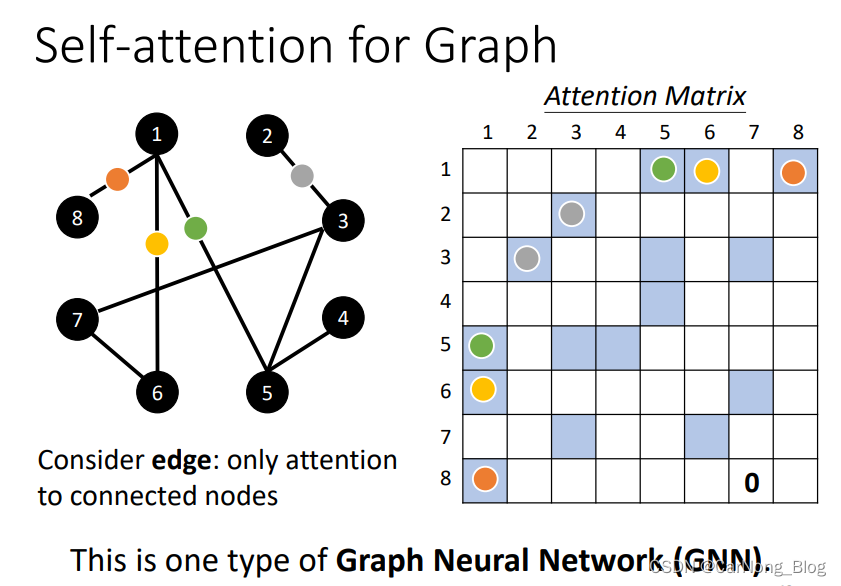
对于Graph来说,其中的每个node,我们都可以表示为一个vector,那么,当我们需要计算Attention Score即相关性分数的时候,我们可以根据Connected nodes 来简化 Attention Score 的计算,如果两个node之间存在边,说明它们是有相关性的,如果没有边,说明相关性几乎为0.
总结
-
Self-Attention 主要是用来解决什么问题?
- 对于一个Sequence的输入(多个vector),我们需要输出多个vector,但是我们不能直接将其分为N个独立分类任务,因为多个vector之间是存在相关性的,它们之间是会相互影响的,不是独立的,通过 Self-Attention 机制,我们可以通过融合上下文的信息来处理这些相关性带来的影响。
-
Self-Attention 的输入可以是输入层,也可以是某些 Hidden Layer 层的输出,多个 Self-Attention Layer 层次之间可以堆叠。
-
Self-Attention 的主要工作机制:
- 每个输入向量需要获取 q、k、v 三个向量,这些向量是通过 Wq、Wk、Wv 三个矩阵计算得出,这三个矩阵的参数是需要学习的参数。
- 通过q、k向量可以获得Attention Score,也就是相关性分数。
- 通过 v 和 Attention Score 相乘,可以得到最终融合了不同权重的上下文信息的输出向量。
-
Self-Attention 很早之前就在一些任务中存在,但是在Transformer架构中发扬光大。
-
Self-Attention 在多个领域中都有应用,比如 NLP CV 等等。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!