采用环形首尾互联互控的雪崩效应极好的Hash算法/杂凑函数RING-512设计原理详解
RING-512密码杂凑算法
黄金龙(QQ1435271638)
什么是Hash算法?
Hash算法,又称为哈希算法、杂凑函数、散列函数、消息摘要算法。它可以将相当长(一般不大于2^64Bit)的输入数据经过计算生成固定长度的Hash值,不同的输入数据对应不同的Hash值(产生碰撞的概率很小)。同时Hash计算的过程是不可逆的,也就是说,由Hash值无法逆推出输入数据。
Hash算法的应用非常多,分别是安全加密、唯一标识、数据校验、散列函数、负载均衡、数据分片、分布式存储、区块链等。
RING-512密码杂凑算法描述
RING-512密码杂凑算法采用类分组密码算法结构,消息分组长度为512bit,摘要长度为512bit。压缩函数状态大小为512bit,共64步,每步更新全部16个寄存器,这加快了算法的雪崩效应。
RING-512密码杂凑算法的初始值
RING-512密码杂凑算法的初始值IV共512bit,由16个32bit字(IV0∽IV15)串联而成,具体值如下:

RING-512密码杂凑算法的常量
RING-512密码杂凑算法的常量为64个32bit字(CN0∽CN63),具体值如下:

RING-512密码杂凑算法的消息填充
对长度为l(l<264)比特的消息m,RING-512密码杂凑算法首先将比特“1”添加到消息的末尾,再添加k个“0”,k是满足(l+k+1)=448Mod512的最小非负整数。然后再添加一个64位比特串,该比特串是消息长度的二进制表示。填充后的消息m`的长度是512 的倍数。

RING-512密码杂凑算法的迭代压缩过程
将填充后的消息m`按512bit进行分组:m`=B(0)B(1)…B(n-1),其中n=(l+k+65)/512。对m`按如下方式迭代:
FOR i=0 TO (n-1)
M(i)=MsgMix(B(i))
V(i+1)=CF(V(i),M(i))
其中CF是压缩函数,V(0)为512 bit初始值IV,B(i)为填充后的消息分组,迭代压缩的结果为V(n)。
MsgMix为消息混乱函数,描述如下:
FOR i=0 TO 15
M[i]=((B[i]+CN[4*i])⊕CN[4*i+1]+ CN[4*i+2])⊕CN[4*i+3];
ENDFOR
RING-512密码杂凑算法的压缩函数
假定A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P为32位寄存器,T0,T1,T2,T3为中间变量,压缩函数V(i+1)=CF(V(i),M(i)),V(0)←IV0||……||IV15,0≤i≤n-1。
状态更新过程描述如下:
ABCDEFGHIJKLMNOP←V(i);
FOR j=0 TO 63
T0=FFFF0(A,B,C,D);
F=F⊕T0+M[1]⊕B;
G=G⊕T0+M[2]⊕C;
H=H⊕T0+M[3]⊕D;
T1=FFFF1(E,F,G,H);
I=I⊕T1+M[4]⊕E;
J=J⊕T1+M[5]⊕F;
K=K⊕T1+M[6]⊕G;
L=L⊕T1+M[7]⊕H;
T2=FFFF2(I,J,K,L);
M=M⊕T2+M[8]⊕I;
N=N⊕T2+M[9]⊕J;
O=O⊕T2+M[10]⊕K;
P=P⊕T2+M[11]⊕L;
T3=FFFF3(M,N,O,P);
A=A⊕T3+M[12]⊕M;
B=B⊕T3+M[13]⊕N;
C=C⊕T3+M[14]⊕O;
D=D⊕T3+M[15]⊕P;
Temp=A;A=B;B=C;C=D;D=E;E=F;F=G;G=H;
H=I;I=J;J=K;K=L;L=M;M=N;N=O;O=P;P=Temp;
ENDFOR
杂凑值为
ABCDEFGHIJKLMNOP←ABCDEFGHIJKLMNOP⊕V(i)
4个混淆扩散函数(FFFF0,FFFF1,FFFF2,FFFF3)
{
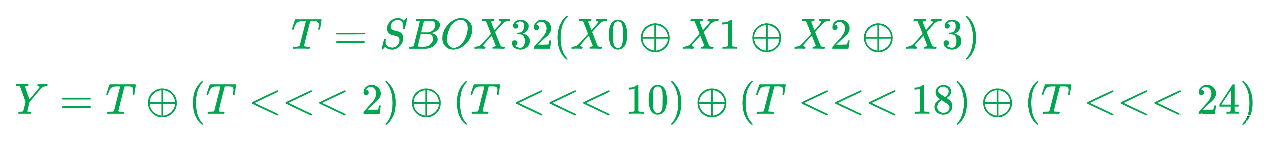
}
Y= FFFF1(X0,X1,X2,X3)
{

}
Y= FFFF2(X0,X1,X2,X3)
{

}
Y= FFFF3(X0,X1,X2,X3)
{

}
SBOX32(Z)=SBOX32(z3||z2||z1||z0)=SBOX(z3)||SBOX(z2)||SBOX(z1)|| SBOX(z0)
SBOX查找表
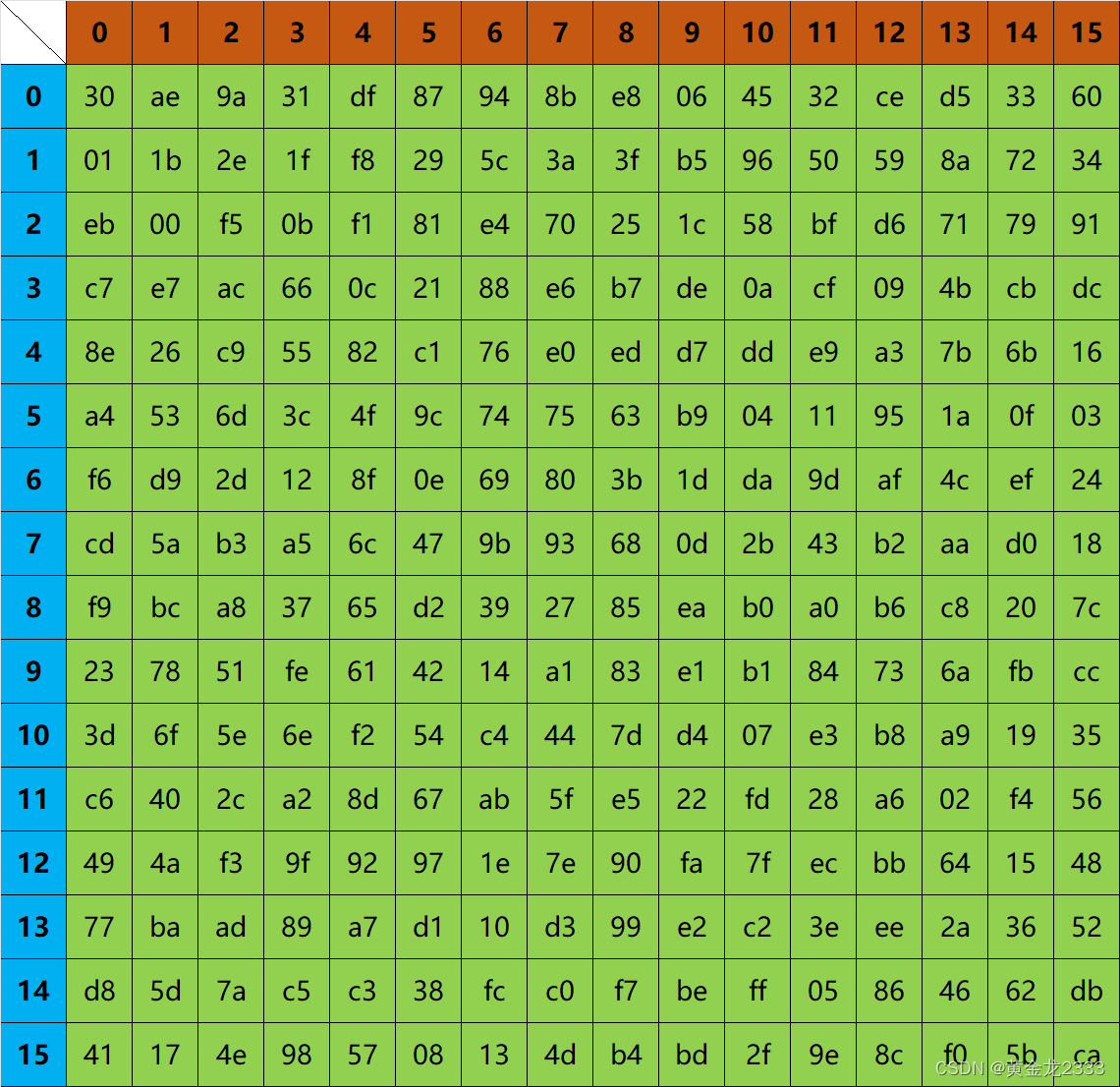
RING-512密码杂凑算法的特点
RING-512密码杂凑算法压缩函数整体结构为类分组密码结构,除了没有消息扩展函数外,还增加了多种新的设计技术,包括使用S盒作为非线性变换、使用了4个不同的加快雪崩效应的混淆扩散函数、每步更新16个寄存器的值等。这样能够有效地避免高概率的局部碰撞,有效地抵抗强碰撞性的差分分析、弱碰撞性的线性分析和比特追踪法等密码分析。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- MS8412:192 kHz 数字音频接收/转换(D/A)电路
- 【STM32】SPI通信
- Halcon区域生长的几种算法regiongrowing/regiongrowing_mean/watersheds
- VMware虚拟机安装小tips
- 在指定页面浏览器窗口发生变化监听并刷新页面
- SIC单晶衬底的常用检测技术
- HDRplus ——简述(一)
- 【Win11】电脑正常联网浏览器却打不开???
- 蓝桥杯备赛 | 洛谷做题打卡day2
- oracle 19c rac集群管理 ------ 日志管理