面试常见的排序算法
发布时间:2024年01月12日
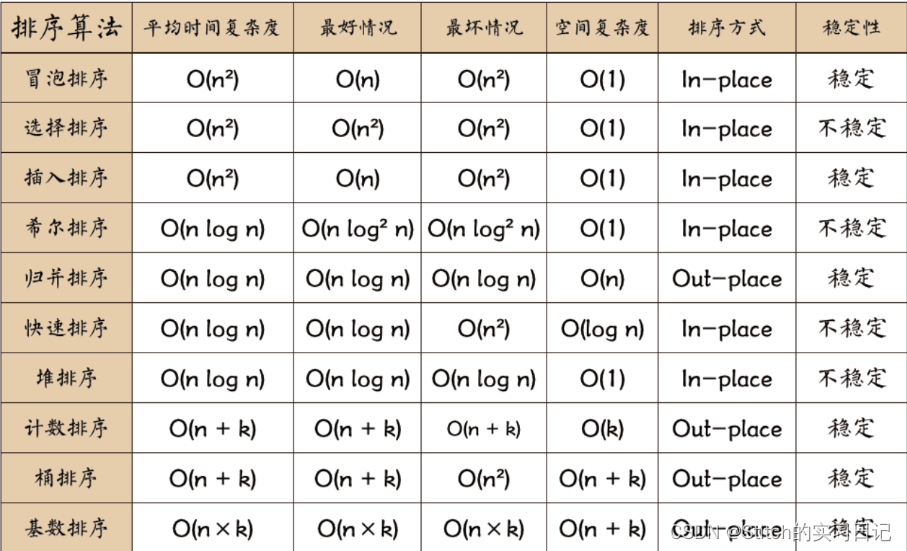
一、各个排序算法的时间复杂度
一、归并排序
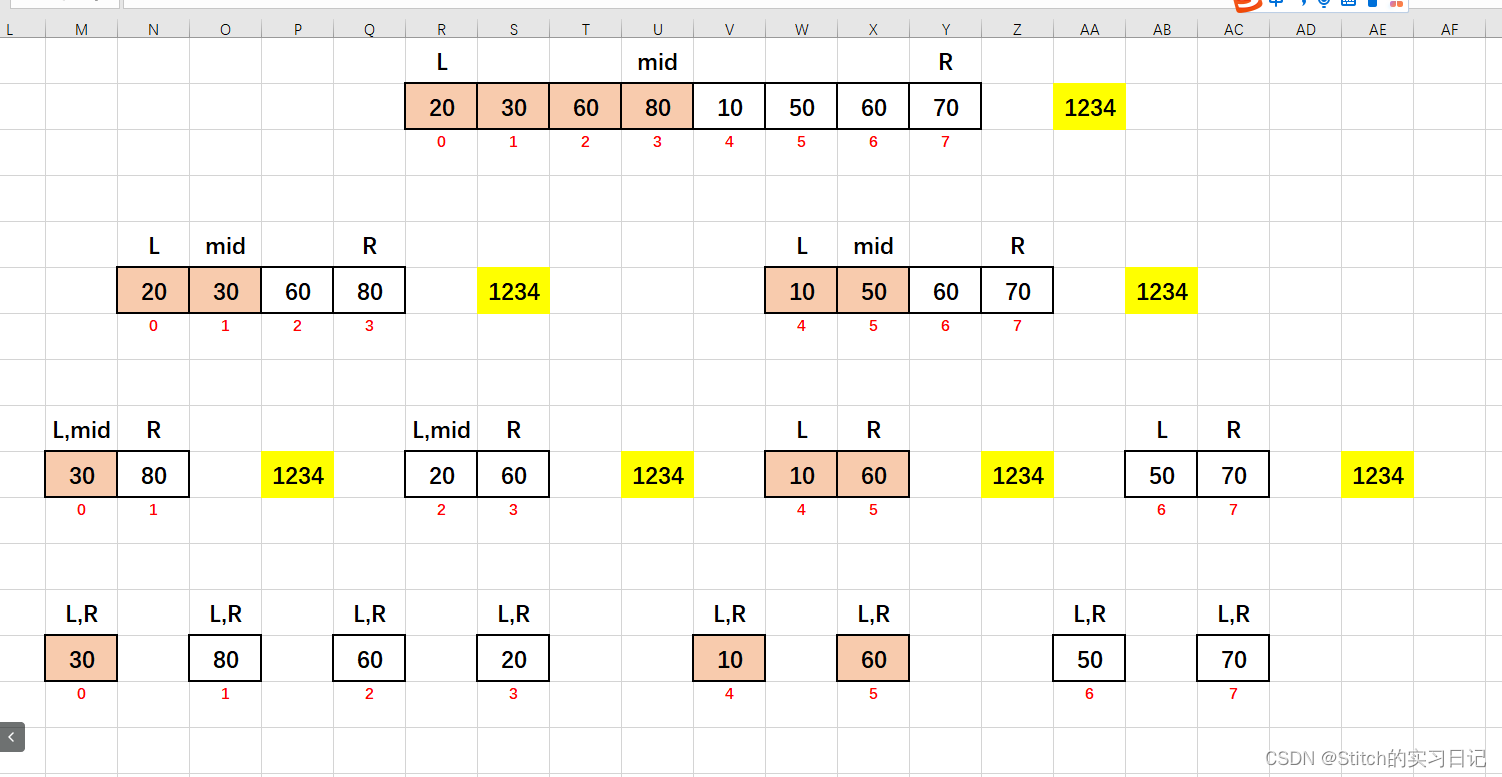
归并思想
思想:将两个有序的数组合并成一个有序的数组。
第一步
将数组进行分解,当分解成单个元素为一组的时候才是组内有序的。
第二步
将两两有序的数组进行合并,将两个有序数组合并成一个有序数组。重复第二步,直至排序完成。
合并的步骤:先申请两数组合并后那么大小的空间,然后将两个排好序的数组逐一进行比较,往申请空间里面放。
 递归前进:自己调用自己的语句
递归前进:自己调用自己的语句
递归回退:return,通过递归结束条件进行回退
在哪里调用的函数,函数的返回值就返回到哪里
#include<iostream>
#include<vector>
using namespace std;
void Merg(vector<int>& vec, int L, int mid, int R) {
vector<int>temp(R-L+1);
int i = L, j = mid + 1;
int index = 0;
while (i <= mid && j <= R) {
if (vec[i] < vec[j]) {
temp[index++] = vec[i++];
}
else {
temp[index++] = vec[j++];
}
}
while (i <= mid) {
temp[index++] = vec[i++];
}
while (j <= R) {
temp[index++] = vec[j++];
}
//把排好序的放回原数组
index = L;
for (auto it:temp) {
vec[index++] = it;
}
}
void Merg_sort(vector<int>& vec, int L, int R) {
if (L >= R) return;
int mid = (R - L) / 2 + L;
Merg_sort(vec, L, mid);
Merg_sort(vec, mid + 1, R);
//合并
Merg(vec, L, mid, R);
}
int main() {
int num;
vector<int>vec;
while (cin >> num) {
vec.push_back(num);
}
Merg_sort(vec,0,vec.size()-1);
for (auto it : vec) {
cout << it << " ";
}
return 0;
}
二、堆排序
第一步:
我们将待排序数组形象成一个堆结构,并将其调整为最大堆
(堆结构:左孩子的下标是2*?i+1,右孩子下标2*i+2)
(最大堆的特点:在这个?堆结构里,任何一个父节点的值都大于其子节点的值)
第二步:
将堆顶元素与待排序数组(假设待排序的数据数量为nums)最后一个元素进行交换,swap(a[0],?a[nums-1]);
第三步:
待排序的数据量减少一个,即num--;将待排序数组重新调整成最大堆结构,重复第二步,循环n-1次,将所有数据排序完成。
初始化堆(将数组调整成最大堆)
从最后一个父节点开始调整(即i?=?n/2-1)
#include<iostream>
#include<vector>
using namespace std;
//将子树调整为最大堆
void Adjust(vector<int>& vec, int start, int end) { //start最开始调整时start不断变化,交换时end不断缩小
int father = start; //当前子树结点
int child = father * 2 + 1; //左子树
while (child <= end) { //不断向下调整防止破坏子树,用end来结束循环防止循环内数组访问越界(调整子树的子树的时候)
if (child + 1 <= end && vec[child] < vec[child + 1]) { //child+1判断右子树是否越界
child++;
}
if (vec[father] < vec[child]) {
swap(vec[father], vec[child]);
//帮助调整子树的最大堆结构,只有和子树的根节点交换了才可能需要向下调整子树
father = child;
child = father * 2 + 1;
}
else {
break; //如果没交换child就会改变 会死循环
}
}
}
//堆排序的整个流程
void Heap_sort(vector<int>& vec)
{
int n = vec.size(); //完全二叉树中结点个数
//最后一个有子节点的下标为n/2-1;
for (int i = n / 2 - 1; i >= 0; i--) {
Adjust(vec, i, n - 1); //end不受限制因为可能破坏子树结构向下调整
}
for (int i = n - 1; i >= 0; i--) //i是下标
{
//交换堆顶和待排序元素中的最后一个元素
swap(vec[0], vec[i]);
//把剩下的待排序元素调整成最大堆结构
Adjust(vec, 0, i - 1); //为啥到i-1,因为Adjust的区间是左闭右闭
}
}
int main() {
vector<int>vec;
int n;
while(cin>>n){
vec.push_back(n);
}
Heap_sort(vec);
for (auto it:vec) {
cout << it << " ";
}
return 0;
}
三、快速排序
1、?在数组中选一个基准数(通常为数组第一个);
2、将数组中小于基准数的数据移到基准数左边,大于基准数的移到右边;
3、对于基准数左、右两边的数组,不断重复以上两个过程,直到每个子集只有一个元素,即为全部有序。
?
#include <iostream>
#include<vector>
#include <algorithm>
using namespace std;
int part(vector<int>& nums, int l, int r) //划分函数
{
int m=l+rand()%(r-l+1);
swap(nums[m],nums[l]);
int i = l, j = r, pivot = nums[l]; //基准元素
while (i < j)
{
while (i<j && nums[j]>pivot) //从右向左开始找一个 小于等于 pivot的数值
{
j--;
}
if (i < j)
{
swap(nums[i++],nums[j]); //r[i]和r[j]交换后 i 向右移动一位
}
while (i < j && nums[i] <= pivot) //从左向右开始找一个 大于 pivot的数值
{
i++;
}
if (i < j)
{
swap(nums[i], nums[j--]); //r[i]和r[j]交换后 i 向左移动一位
}
}
return i; //返回最终划分完成后基准元素所在的位置
}
void Quicksort(vector<int>& nums, int l, int r)
{
int mid;
if (l < r)
{
mid = part(nums, l, r); // 返回基准元素位置
Quicksort(nums, l, mid - 1); // 左区间递归快速排序
Quicksort(nums, mid+1, r); // 右区间递归快速排序
}
}
int main()
{
vector<int> vec;
int n;
while(cin>>n){
vec.push_back(n);
}
Quicksort(vec, 0, vec.size()-1);
for (auto it:vec) {
cout << it << " ";
}
return 0;
}
四、冒泡排序
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
针对所有的元素重复以上的步骤,除了最后一个。
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
#include<stdio.h>
#include<iostream>
using namespace std;
void swap(int* a, int* b) {
int c = *a;
*a = *b;
*b = c;
}
void BubbleSort(int arr[],int n) {
for (int i = 1; i < n; i++) {
int flat=0;
for (int j = 0; j < n - i; j++) {
if (arr[j] > arr[j + 1]) {
swap(&arr[j], &arr[j + 1]);
flat=1;
}
}
if(flat==0){
return;
}
}
}
int main() {
int n;
cin >> n;
int arr[n];
for (int i = 0; i < n; i++) {
cin >> arr[i];
}
BubbleSort(arr, n);
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
return 0;
}
?
?
?
?
?
?
文章来源:https://blog.csdn.net/qq_57106289/article/details/135497388
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- ESP32应用篇 一、 用VSCode platformIO 代替Arduino
- 企业怎么打造私域转化闭环?
- 如何控制项目管理中的日程冲突?
- 代码随想录27期|Python|Day15|二叉树|层序遍历|对称二叉树|翻转二叉树
- 百度飞桨文心生态成果最新披露:开发者达1070万 模型数超86万
- 苹果上架商城被拒原因问题排查解决
- 深入理解java中Classpath 和类加载机制
- 【守护工地安全】YOLOv8实现安全帽检测
- 研究生开题报告撰写:文言一心VSChatgpt3.5
- K-均值聚类(K-means clustering)