【算法】使用二分查找解决算法问题:理解二分法思想,模板讲解与例题实践
文章目录
二分算法思想 / 性质 / 朴素模板
二分查找的引入(二段性)
- 首先,关于二分的题,重点在于理解二分法思想,当理解后,模板自然便可写出来,变成简化思路的工具。
- 我们通过下面的一道题,理解二分查找算法思想(并简单了解所谓模板):
704.二分查找

对于该题,我们首先思考 暴力解法:
- 很简单,遍历数组,如果找到该数则返回下标,否则返回-1
- 我们知道:当数组元素很多时,或每次目标值与起始位置很远时,暴力解法的时间开销是很大的。
此时我们引入一个思考:
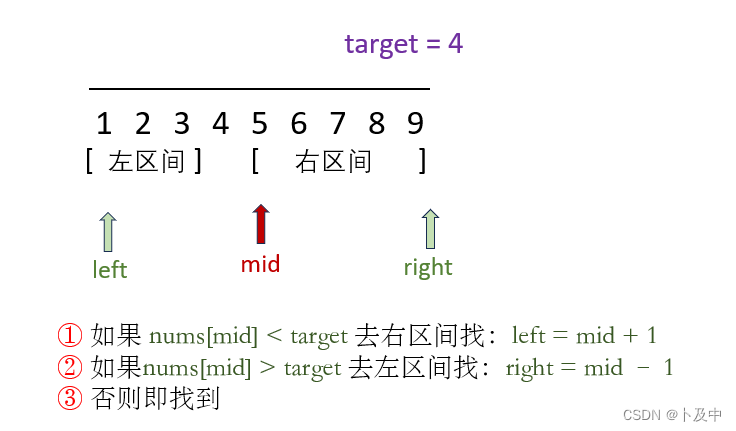
- 当我们在数组中随机选取一个数x:
- 如果x<target,那么目标值一定在x后面(x前面的数就不用再看了);
- 当x>target,我们就可以直接去前面找目标值。
- 此时数组就被分成了两部分,即x前面的部分和x后面的部分,我们跟随查找条件直接去到相应的区间即可。
- 我们可以感知到题目由x与target的关系被分成了两段,这就是二段性。
- 当一个题目有二段性的时候,我们可以采用二分法解题。
代码:
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0, right = nums.size() - 1; // 左右区间边界
while(left <= right)
{
int mid = left + (right - left + 1) / 2; // 更新 mid
if(nums[mid] < target) // 当前值<目标值 : 更新左边界
left = mid + 1;
else if(nums[mid] > target) // 当前值>目标值 : 更新右边界
right = mid - 1;
else // 找到目标值,返回下标
return mid;
}
return -1; // 未找到,返回-1
}
};
上面的代码很好理解:
- 当左指针未超过右指针时,每次更新中间指针mid,通过nums[mid] 与 target的关系比,更新左右边界,直到找到target
模板
当我们理解了二分思想,对于一道题,重点在于分析出该题具有二段性,随后写代码就不是难事了,但这里还是简单写出朴素模板:
while(left <= right)
{
int mid = left + (right - left + 1) / 2;
if(...) // 根据题意左右边界的更新也有所不同
left = mid + 1;
// left = mid;
else if(...)
right = mid - 1;
// right = mid;
else
return ...;
}
这里需要注意的是mid 的更新:
-
平时我们有
mid = (left + right) / 2写法来进行中间值的更新,这里不提倡这种写法。因为当right和left过大,这种写法会造成整形溢出。 -
而对于
mid = left + (right - left + 1) / 2与mid = left + (right - left) / 2,是否+1,我们分为下面的情况
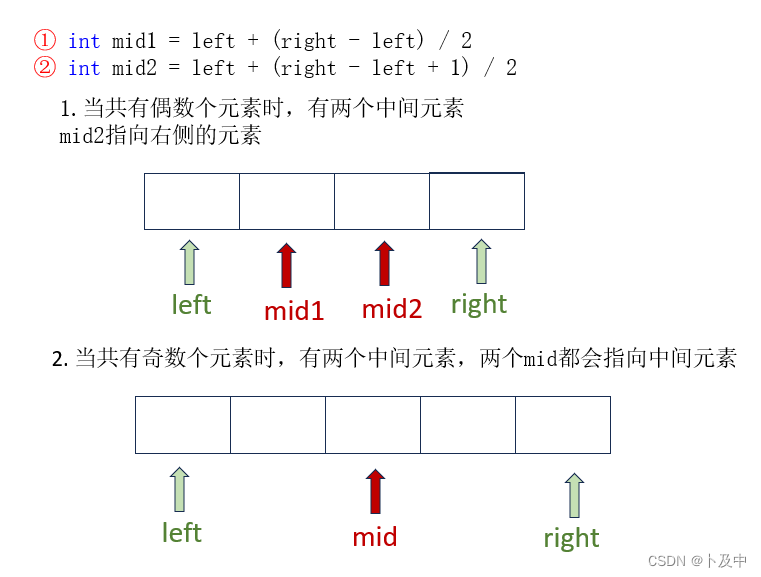
-
那么我们什么时候采用法①或采用法②?
- 当代码下面出现“-1”的时候,我们更新mid时就“+1”。
- 即当我们有了后续更新left、right边界后,通过判断是否有mid - 1,在求中间值时是否将
(right - left + 1)部分改为(right - left + 1)。
-
我们通过下面的一道题来理清二分查找的细节处理。
34.在排序数组中查找元素的第一个和最后一个位置

思路
- 题目给出了一个非递减顺序的数组(即要么递增要么重复),要求O(logn)的时间复杂度,这两点其实就可以想到要用二分了(
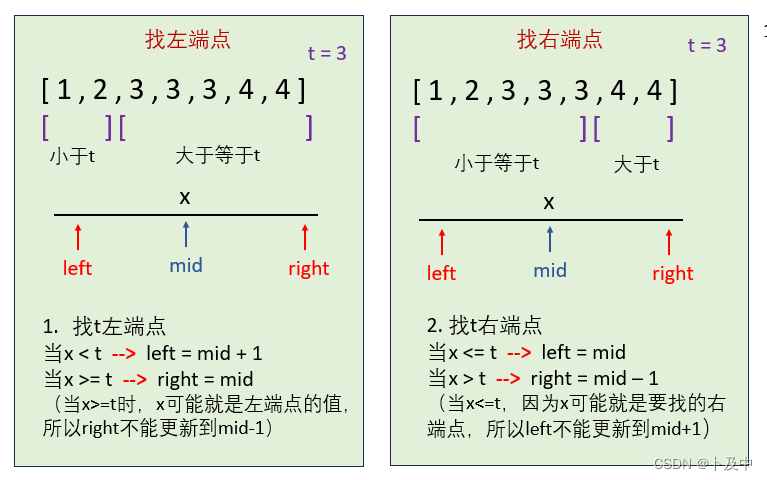
- 根据题目要求,我们需要找到目标值的左右端点:
- 找左端点,数组被分成两部分:① 小于t ② 大于等于t
- 找右端点,数组分为两部分:① 小于等于t ② 大于t
- 这样分组可以让我们通过更新区域来找到端点
- 此时题目有明显的二段性,我们可以使用二分查找来解题
- 由于此题为了解释二分代码的细节问题,会花篇幅进行细节解释:
细节问题
-
首先关于循环条件:使用left < right 而不是 <=。
-
关于求中点的操作:
我们直接选取一个极端情况:当区间只剩下两个元素时。- 对于找左端点的情况
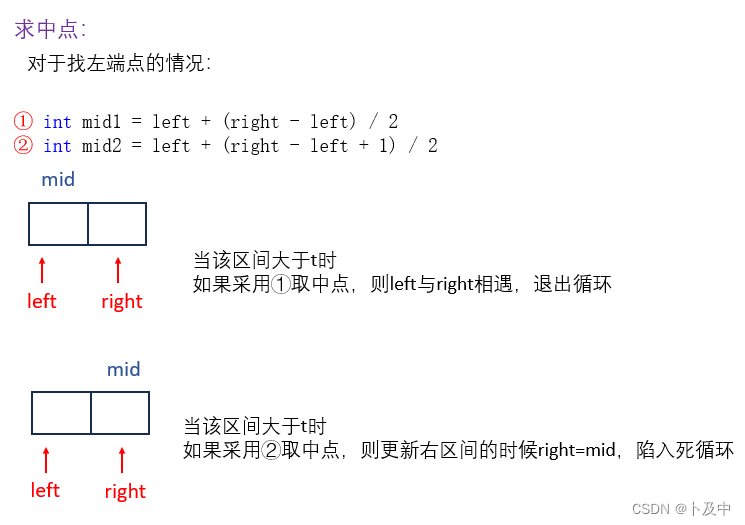
由上图我们知道,当找左端点时:应该使用①进行求中点操作。
- 对于找左端点的情况
-
左右区间的更新
- 对于求左端点的情况:

- 对于求右端点的情况:

- 对于求左端点的情况:
代码
vector<int> searchRange(vector<int>& nums, int target) {
// 处理边界情况
if(nums.size() == 0) return {-1, -1};
// 二分查找
int left = 0, right = nums.size() - 1;
// 1. 找左区间端点
while(left < right)
{
int mid = left + (right - left) / 2;
if(nums[mid] < target) left = mid + 1;
else right = mid;
} // left与right相遇找到左区间端点
int begin = 0;
if(nums[left] != target) return {-1, -1};
else begin = left;
// 2. 找右区间端点
right = nums.size() - 1;
while(left < right)
{
int mid = left + (right - left + 1) / 2;
if(nums[mid] <= target) left = mid;
else right = mid - 1;
}
// int end = right;
return {begin, right};
}
二分查找的前提条件 / 时间复杂度分析
使用条件
-
二分查找算法必须在有序的序列中才能使用。
-
二分查找的核心思想是通过比较中间位置的元素与目标元素的大小关系,确定目标元素可能存在的区域。如果数组是无序的,那么就无法保证中间位置的元素与目标元素的大小关系。
时间复杂度
二分查找的每一次迭代中,会将查找区域划分为两个子区域,并通过比较中间位置的元素与目标元素的大小关系,确定目标元素可能存在的区域。这样,每一次迭代都能将查找区域缩小一半。
假设要查找的数组长度为n,每次迭代后查找区域的长度会减少一半,直到找到目标元素或者确定目标元素不存在。因此,最坏情况下,二分查找的迭代次数为 k,满足 n / 2^k = 1。
通过求解上述方程可以得到 k = log2(n),即二分查找的时间复杂度为 O(log n)。
算法题
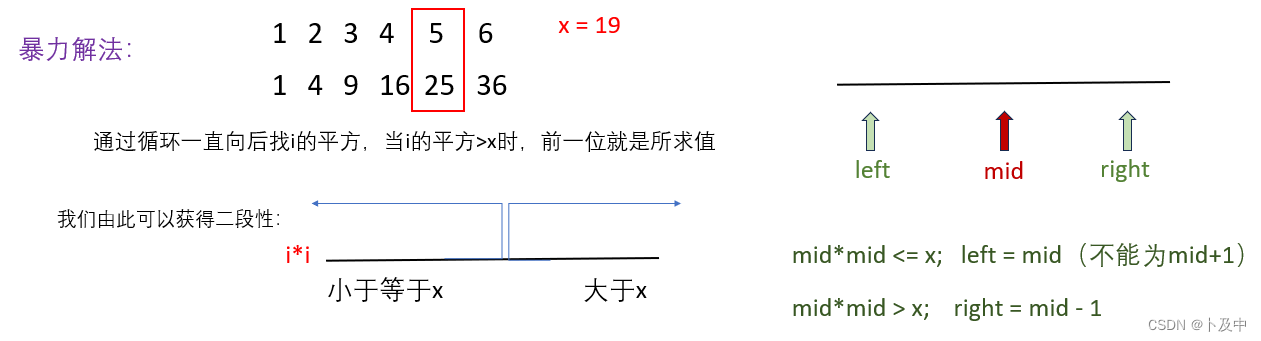
69.x的平方根

- 如图将数组分为 小于等于x 和 大于x 两段区间
- 根据二分法:
- mid 的平方小于等于 x,则更新 left 为 mid
- mid 的平方大于 x,则更新 right 为 mid - 1
思路
代码
int mySqrt(int x) {
// 处理边界情况
if(x < 1) return 0;
long long left = 0, right = x;
// 二分法
while(left < right)
{
long long mid = left + (right - left + 1) / 2;
if(mid * mid <= x) left = mid;
else right = mid - 1; // 出现mid-1,上面求mid用"+1"
}
return (int)left;
}
35.搜索插入位置

思路
- 根据题目:排序数组、返回索引,O(logn)的算法,此时大概率可以用二分解题

代码
- 写代码时注意几点:根据上文介绍的,由我们更新left,right的方式,while循环中写left < right
- 当循环结束后,有两种可能:
- 找不到target:则target应该插入到数组外,即下标为left+1
- 找到了:left即为待插入位置
int searchInsert(vector<int>& nums, int target) {
// 二分法
int left = 0, right = nums.size() - 1;
while(left < right)
{
int mid = left + (right - left) / 2;
if(nums[mid] < target) left = mid + 1;
else right = mid;
}
if(nums[left] < target) return left+1; // 数组中无target,插入位置在数组外
else return left; // 数组中有t / 无t+插入位置在数组内
}
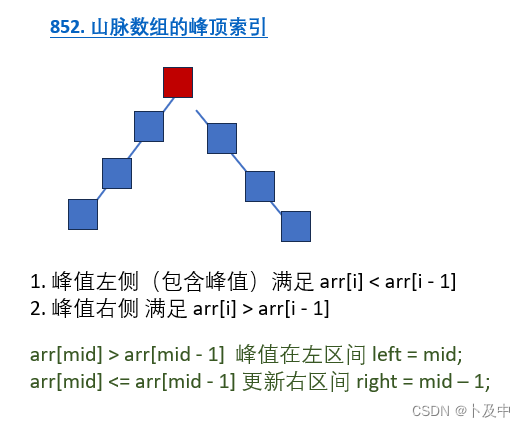
852.山脉数组的峰顶索引

思路
- 题目看起来比较模糊,通过看示例基本可以理解,简单理解就是:数组存在一个峰值,峰值左边的数是递增的,峰值右边的数是递减的。
代码
int peakIndexInMountainArray(vector<int>& arr) {
int left = 0, right = arr.size() - 1;
// 峰值左侧区间 arr[i] > arr[i-1] 向右找 left = mid;
// 峰值右侧区间 arr[i] < arr[i-1] 向左找 right = mid - 1;
while(left < right)
{
int mid = left + (right - left + 1) /2;
if(arr[mid] > arr[mid-1]) left = mid;
else right = mid - 1;
}
return left; // 返回峰值索引
}
162.寻找峰值

思路

代码
int findPeakElement(vector<int>& nums) {
int left = 0, right = nums.size() - 1;
// 取下标i,如果有num[i] > nums[i+1] 这两个数是递减,则这两数左侧必定存在一个峰值
// 如果nums[i] < nums[i] 则右侧一定存在峰值
while(left < right)
{
int mid = left + (right - left) / 2;
if(nums[mid] > nums[mid + 1]) right = mid;// 找左区间
else left = mid + 1;
}
return left;
}
153.寻找旋转排序数组中的最小值

思路

代码
int findMin(vector<int>& nums) {
int n = nums.size();
int left = 0, right = n - 1;
// 最小值的左侧区间,nums[i] < nums[n-1] 成立
// 右侧区间,nums[i] > nuns[n-1] 成立
// 二段性->二分法
while(left < right)
{
int mid = left + (right - left) / 2;
if(nums[mid] > nums[n-1]) left = mid + 1;
else right = mid;
}
return nums[left];
}
LCR173.点名

思路
- 实际就是找0~n-1中缺失的一个数字
- 由于数组中少了一个数字,我们可以知道:
- 在缺少的数字x左侧,满足:值==下标
- 缺少的数字x右侧,满足:值>下标(即值==下标+1)
- 据此得到二段性,可以使用二分法
- 值得一提的事,这道题解法很多,哈希、位运算、直接遍历、数学方式等,都可以尝试。
代码
int takeAttendance(vector<int>& records) {
// 缺失的数左区间满足:值=下标
// 缺失的数右区间满足:值>下标
// 二段性->二分法
int n = records.size();
int left = 0, right = n - 1;
while(left < right)
{
int mid = left + (right - left) / 2;
if(records[mid] == mid) left = mid + 1;
else right = mid;
}
// 处理边界情况:当确实的数为n的时候
if(records[right] == right) return n;
return right;
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- VisualODX——ODX数据自动转换工具 加快开发进度
- 全人类知识共享:你或许没想到的三个问题
- [其他] VS Code 配置 Source Insight 主题
- 一文了解软件测试
- 谷歌和微软的ASR的差异和特点
- iOS 17.2系统获取IDFA时不弹窗问题
- 2023国产电影翻拍观察:国外的月亮,国内阴晴圆缺
- 安科瑞汽车充电桩在西北地区的应用——安科瑞 顾烊宇
- deepin20.9设置root登录
- CRM系统对中小企业有哪些好处?为什么中小企业要用CRM?