724. 寻找数组的中心下标

代码：

class Solution {
    public int pivotIndex(int[] nums) {
        int last=0;    //放前一个下标的左右差值
        int now=0;     //放当前下标的左右差值

        // 0 位于边界，先算出 0 下标左右的差值
        for(int i=1;i<nums.length;i++){
            last+=nums[i];
        }

        //判断是否 0 下标就已经是中心下标
        if(last==0){
            return 0;
        }

        //获取各个下标左右两边的差值
        for(int i=1;i<nums.length;i++){
            now=last-nums[i]-nums[i-1];
            if(now==0){
                return i;
            }
            last=now;
        }

        return -1;
    }
}

题解：

? ? ? ? 本题的意思很简单，我们需要找到一个中心下标，中心下标左边和右边的数据和是相等的，在遇到一个题时，我们先想一下它的暴力解法，因为优化解法通常是由暴力解法演化而来的

? ? ? ? 本题的暴力解法也很简单，我们可以去求每个下标左右两边的数据和是否相等，每判断一次下标就需要遍历一次数组，而我们最多要判断 n 次，所以时间复杂度为 O（n），这是一个比较大的复杂度了，我们要想一个优化解法

? ? ? ? 要判断左右两边的数据是否相同，我们可以判断左右两边的数据和之差是否为 0 ，如果为 0 ，就说明左右两边的数据和相同，我们可以利用数组 dp 来存储对应下标左右两边的数据和之差，如 dp[ i ] ,就代表 i 下标左右两边的数据和之差，当 dp[ i ] = 0 时就代表? i 下标左右两边的数据和相同，i 下标就为中心下标

? ? ? ? 现在我们要探究的就是如何填充 dp 数组，我画了下面的图方便理解

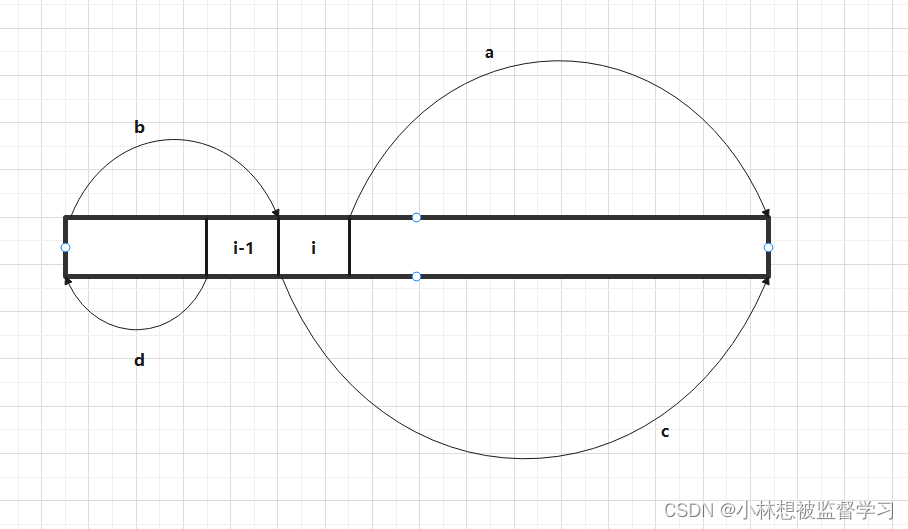
? ? ? ? 如上图，我们要获取 dp[ i ]?的值就需要 a - b, a = c -?nums[ i ],b = d?+ nums[ i-1 ],所以 a - b =

c -?nums[ i ] - d -?nums[ i-1 ] ，而 c - d =?dp[ i-1 ]，所以?dp[ i ] =?dp[ i-1 ]?-?nums[ i ] ?-?nums[ i-1 ]，

我们通过上面的式子从左到右便可以填充完 dp 数组

? ? ? ? 要注意，我们首先要计算 dp[ 0 ] 的值，因为当 i =0 时，在该式子中会出现 -1 下标，这是越界的，所以我们先要计算出 0 下标左右两边数据和的差值，再从左到右填充 dp 数组，当 填充到 dp 数组中的值为 0 时，就找到了中心下标

? ? ? ? 实际上，我们在填充 dp 数组时，只需要 dp 前一个下标的值，并且只要 dp 数组中的值出现 0 就不需要遍历了，所以我们直接可以用两个变量，一个记录当前下标的两边数据和的差值，一个记录前一个下标两边数据和的差值，就能代替 dp 数组