代码随想录算法训练营Day11 | 144.二叉树的前序遍历、145.二叉树的后序遍历、94.二叉树的中序遍历
发布时间:2023年12月27日
LeetCode 144 二叉树的前序遍历
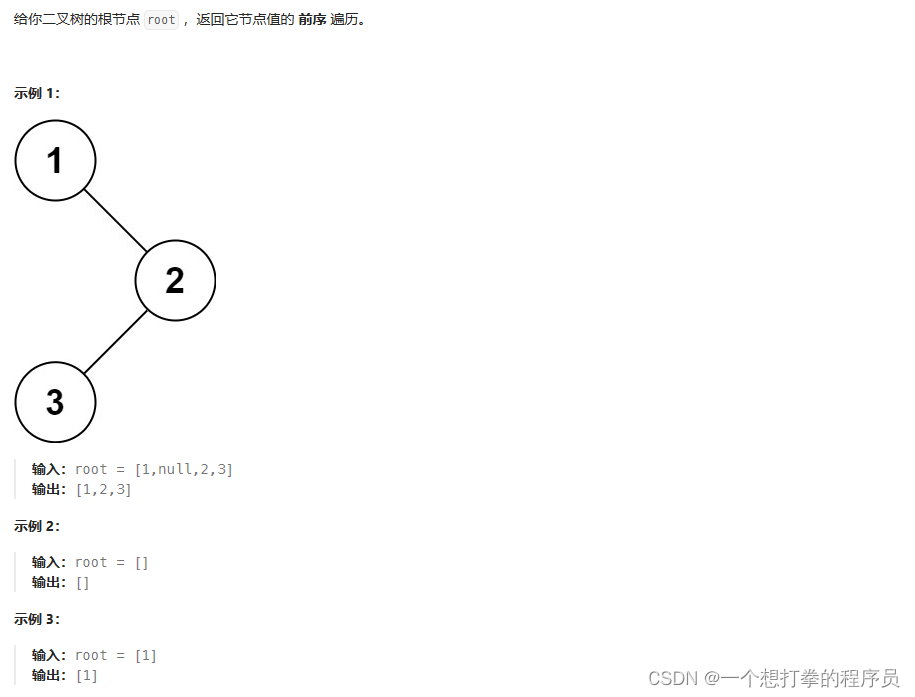
本题思路:有两种写法,一种是递归写法,一种是迭代的写法。我们一一来讲解这两种写法。
前序遍历递归写法
二叉树的前序遍历的顺序是: 根 左 右
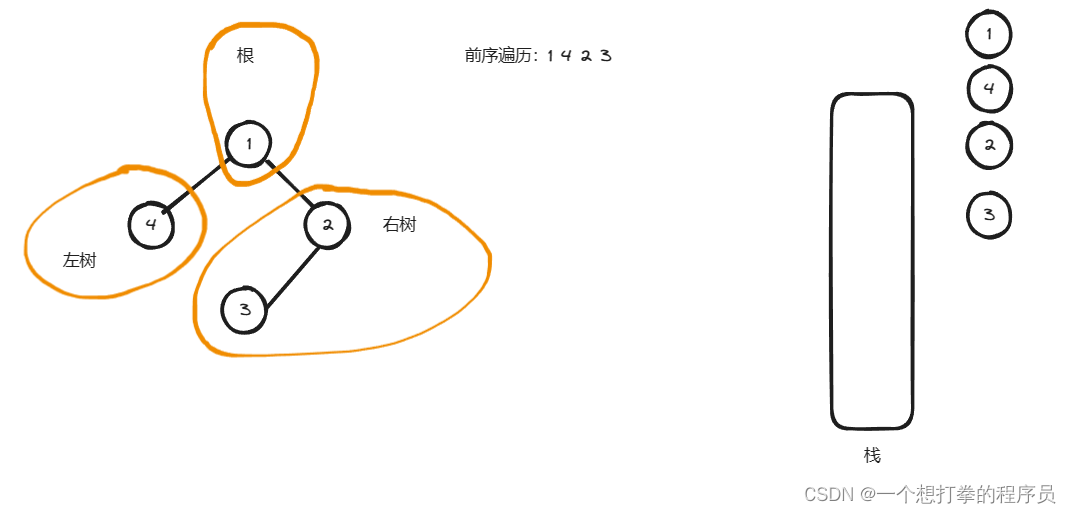
我们将一根树看成 左 根 右 三个部分!,我们利用一个整体的思维,将一颗树,看成一个根,左树、右树。如下图所示。
此时我们要遍历的话,先整体遍历根,然后遍历左树,再遍历右树。 此时得到的顺序就是 根左右。
public class preorder {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> list = new LinkedList();
preoder(root, list);
return list;
}
// 前序遍历
public void preoder(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
list.add(root.val); // 先遍历根
preoder(root.left, list); // 遍历左树
preoder(root.right, list); // 遍历右树
}
}
前序遍历迭代写法
迭代遍历的话,我们需要借助栈来实现。利用栈的特性来完成这个前序遍历。
我们来演示下思路,利用图片的形式。
- 首先将根节点入栈得到下图
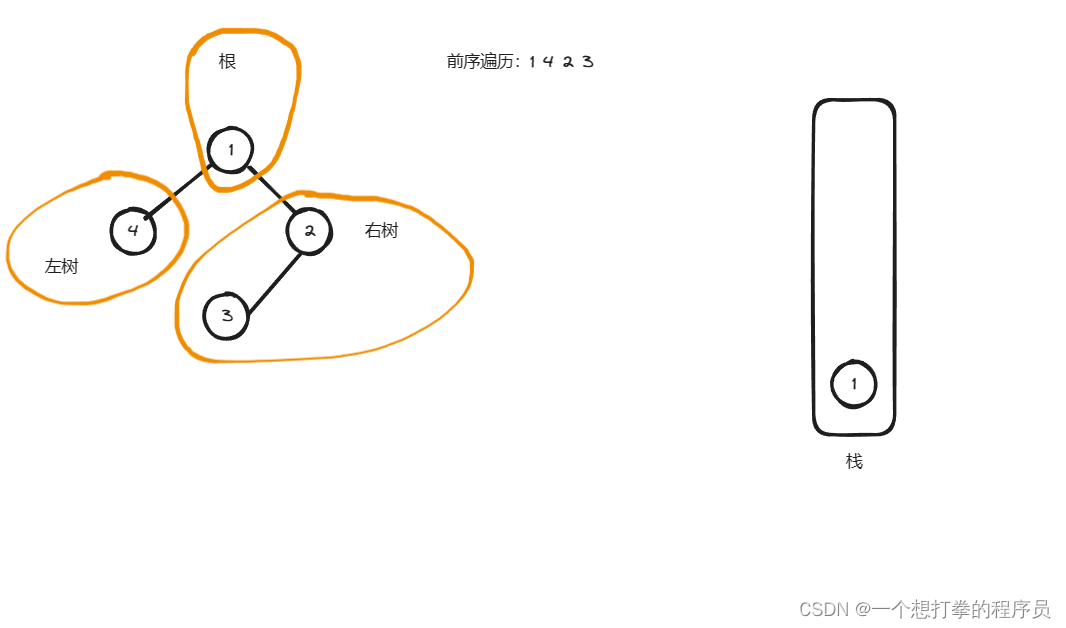
- 然后就是弹出栈顶元素1,记录到 list 中,然后判断该节点是否有左右孩子,如果有就加入。此处有个问题,我们应该先入左孩子,还是右孩子。
- 如果是先入左孩子,再入右孩子,那么弹出的时候就是右孩子。
- 如果是先入右孩子,再入左孩子,那么弹出的时候就是左孩子。
- 通过分析,我们想要的是 根 左 右 这种顺序。所以应该先入右孩子,再入左孩子。
- 所以我们判断 节点1 左右孩子都有,先入右,再入左,得到下图
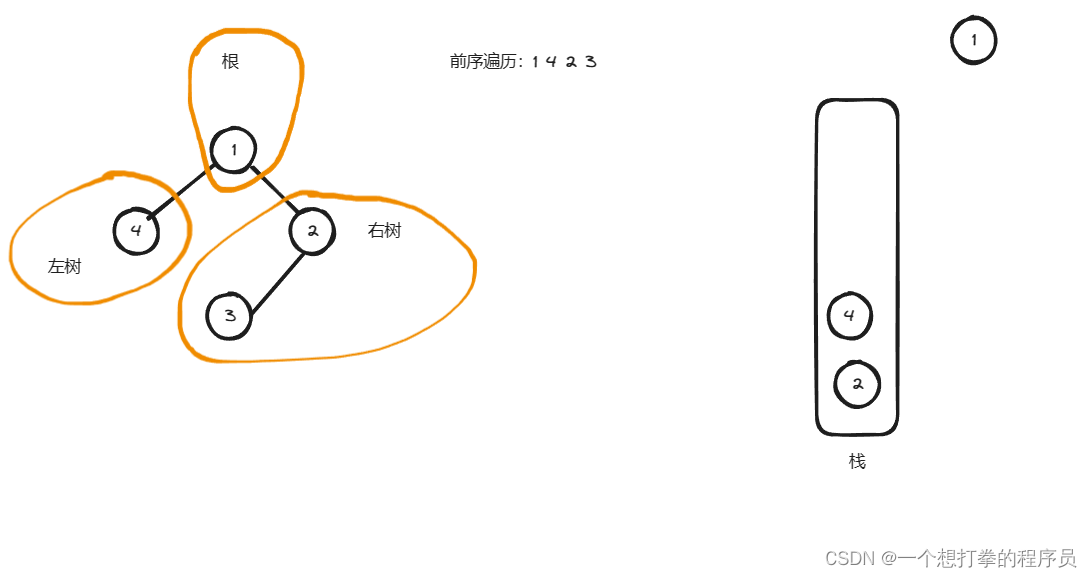
- 接着弹出栈顶元素 4,记录到list中,然后判断是否有左右孩子,通过上图,发现没有,得到下图
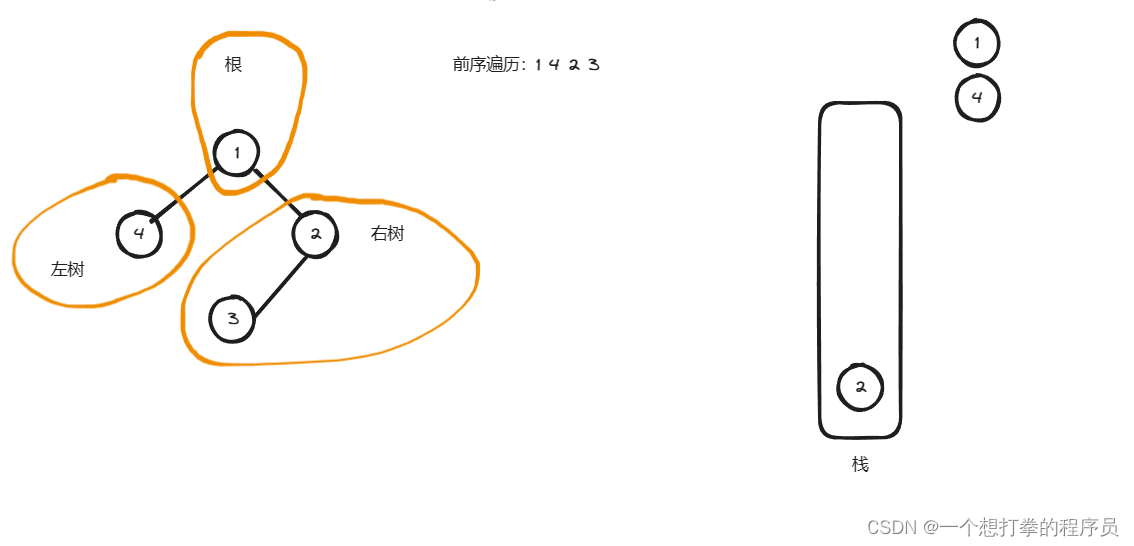
- 继续弹出栈顶元素2,记录到list中,然后判断是否有左右孩子,并加入,得到下图

- 继续弹出栈顶元素3,记录到list中,然后是否有左右孩子 ,并加入,得到下图
- 最后栈为空的时候,结束
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
Stack<TreeNode> stack = new Stack();
List<Integer> list = new LinkedList<>();
if(root == null){
return list;
}
// 先将根节点进栈
stack.push(root);
while(!stack.isEmpty()){
TreeNode cur = stack.pop();
list.add(cur.val);
// 如果右孩子不为空,则就入栈
if(cur.right != null){
stack.push(cur.right);
}
// 如果左孩子不为空,则入栈
if(cur.left != null){
stack.push(cur.left);
}
}
return list;
}
}
LeetCode 145 二叉树的后续遍历
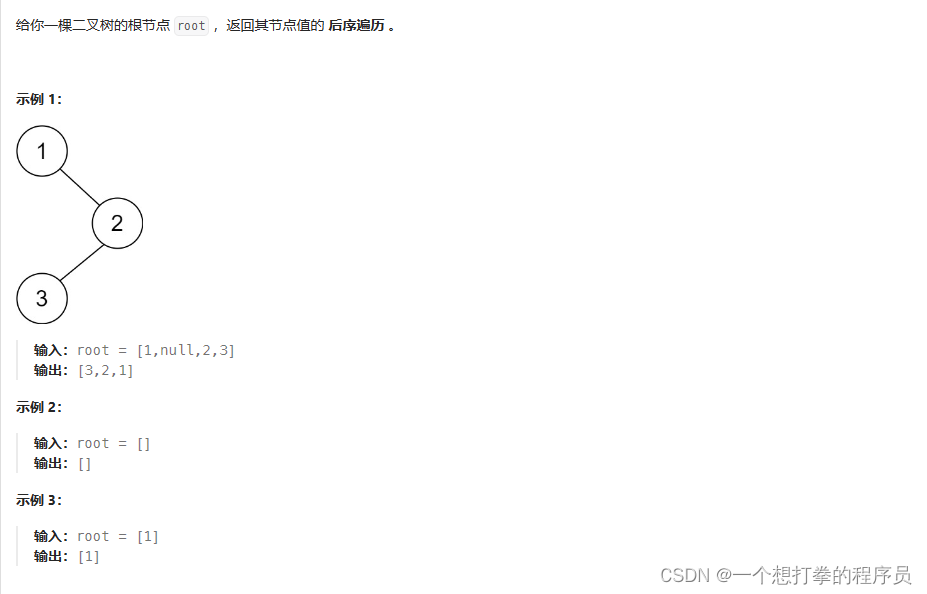
本题思路:一种是递归版本,一种是迭代版本。下面一个一个讲解下思路。
二叉树的后序遍历的顺序是: 左 右 根
后序遍历递归写法
我们将一根树看成 左 根 右 三个部分!,我们利用一个整体的思维,将一颗树,看成一个根,左树、右树。如下图所示。
此时我们要遍历的话,先整体遍历左树,然后遍历右树,再遍历根。 此时得到的顺序就是 左右根。
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> list = new LinkedList();
postorder(root,list);
return list;
}
public void postorder(TreeNode root, List<Integer> list){
if(root == null){
return;
}
postorder(root.left,list);
postorder(root.right,list);
list.add(root.val);
}
}
后序遍历迭代写法
上一题,我们进栈的顺序是,根 右 左,所以得到最终前序遍历顺序是 根左右,如果我们换一换,将入栈顺序改成 根 左 右, 此时得到的顺序就是 根 右 左。 我们再逆置一下,就是 左 右 根,这不就是我们想要的结果了吗。
所以只需要对上述代码修改三行即可
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
Stack<TreeNode> stack = new Stack();
List<Integer> list = new LinkedList<>();
if(root == null){
return list;
}
// 先将根节点进栈
stack.push(root);
while(!stack.isEmpty()){
TreeNode cur = stack.pop();
list.add(cur.val);
// 如果左孩子不为空,则入栈
if(cur.left != null){
stack.push(cur.left);
}
// 如果右孩子不为空,则就入栈
if(cur.right != null){
stack.push(cur.right);
}
}
// 逆置顺序
Collections.reverse(list);
return list;
}
}
LeetCode 94 二叉树的中序遍历

本题思路:一种是递归版本,一种是迭代版本。下面一个一个讲解下思路。
二叉树的中序遍历的顺序是: 左 根 右
中序遍历递归写法
我们将一根树看成 左 根 右 三个部分!,我们利用一个整体的思维,将一颗树,看成一个根,左树、右树。如下图所示。
此时我们要遍历的话,先整体遍历左树,然后遍历根,再遍历右树。 此时得到的顺序就是 左根右。
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> list = new LinkedList();
inorder(root,list);
return list;
}
public void inorder(TreeNode root, List<Integer> list){
if(root == null){
return;
}
inorder(root.left,list);
list.add(root.val);
inorder(root.right,list);
}
}
中序遍历迭代写法
迭代写法的话,我们仍旧是利用栈,但是不能和前面两种一样,简单的调换下代码顺序就能实现了。
同样我们用一个图,来分析一下具体的一个思路。
- 最初始的状态下

- 然后将根节点入栈,并且一直找左孩子,如果有左孩子就入栈,直到左孩子为空,得到下图
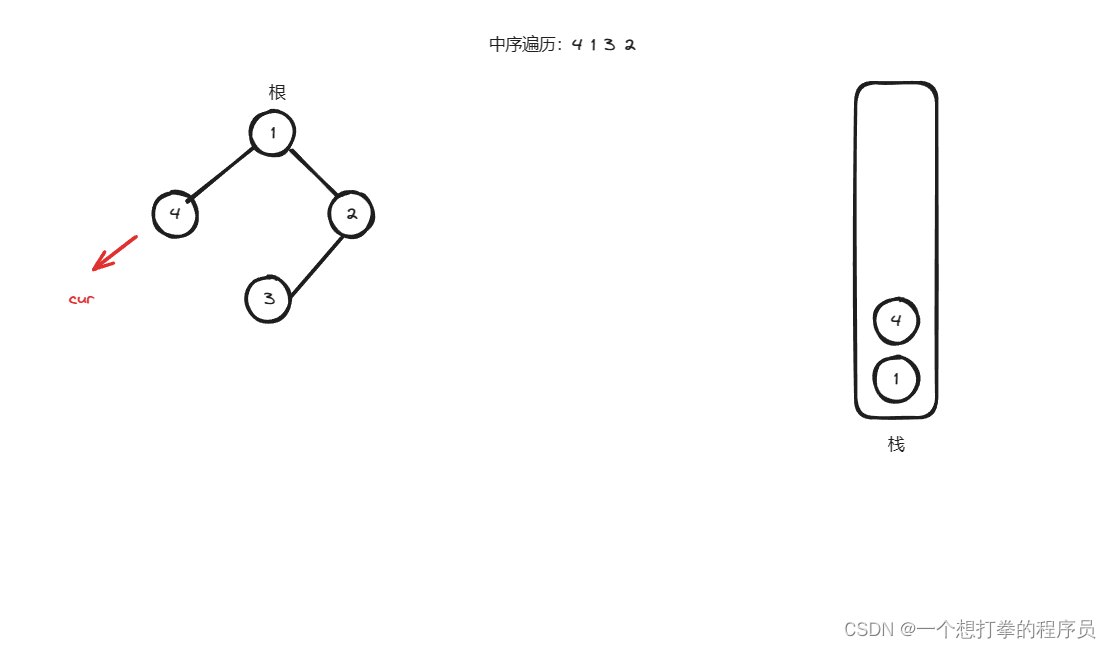
- 根据上图,此时 cur 为空,就弹出栈顶元素,并记录到 list ,并且判断是否有 右孩子,为什么是只判断是否有右孩子,因为此时左孩子已经判断过了。如果有右孩子,就让 cur 指向 右孩子,得到下图
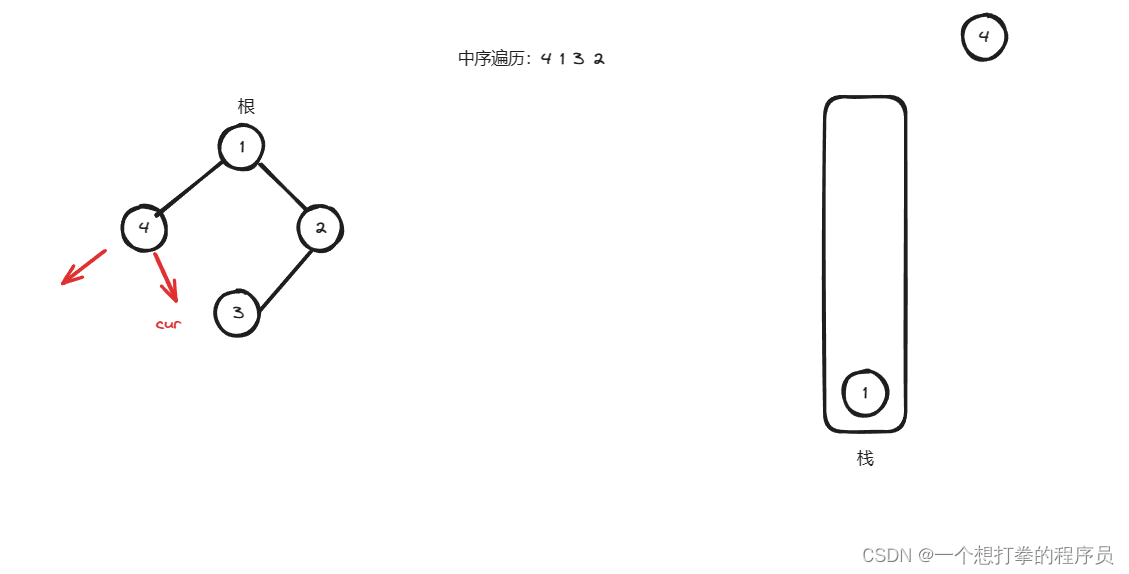
- 根据上图,然后判断 cur 是否为空,如果为空,就弹出栈顶元素用cur来接收,并记录到 list ,并且 cur 往右边移动 cur = cur.right,得到下图
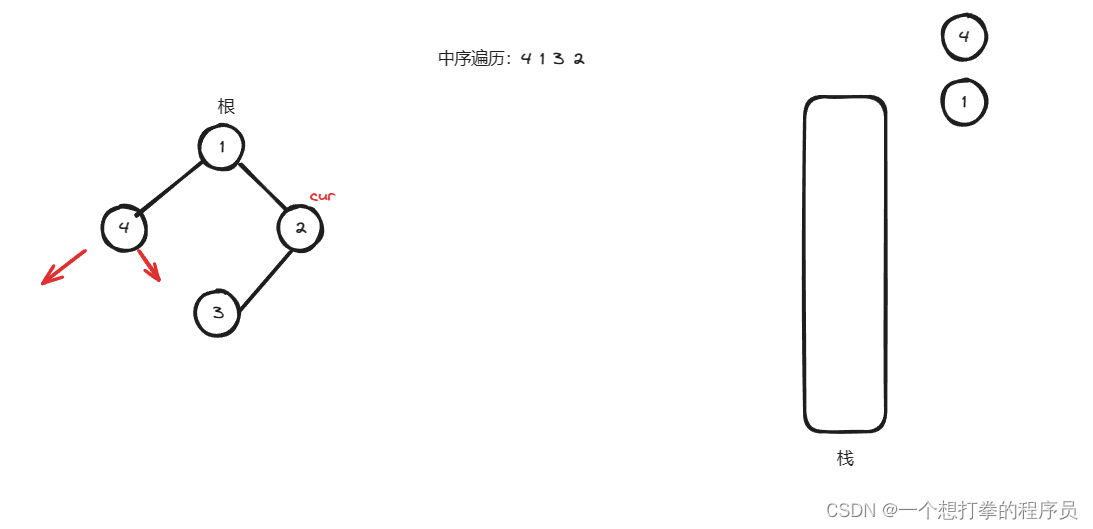
- 根据上图,然后判断 cur 不为空,并且 cur.left 也不为空,一直添加入栈,直到 cur 为空,得到下图
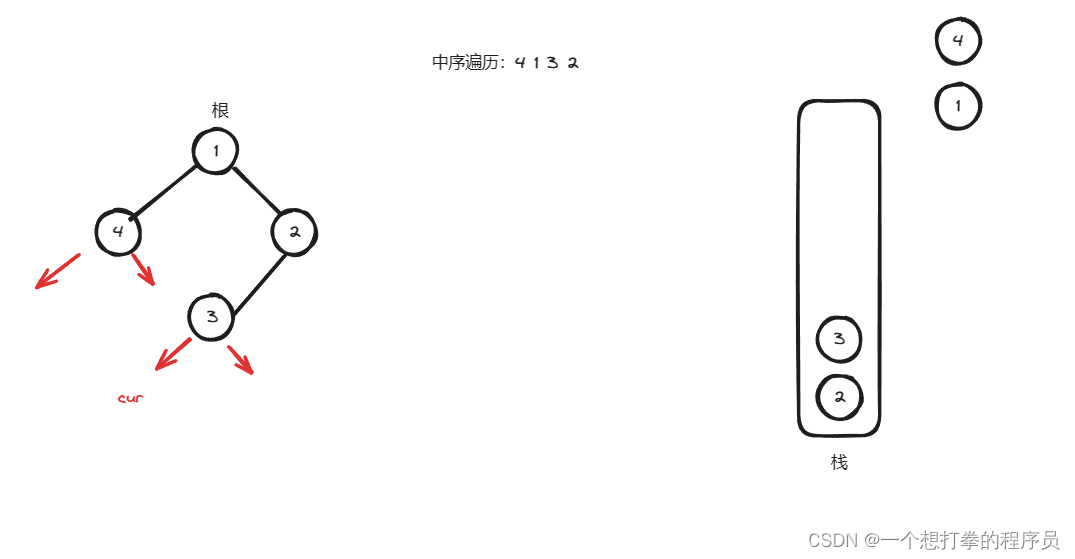
- 根据上图,此时 cur 为空,所以弹出栈顶元素,用 cur 接收,并记录到 list 中,然后将 cur = cur.right,发现仍然为空,得到下图
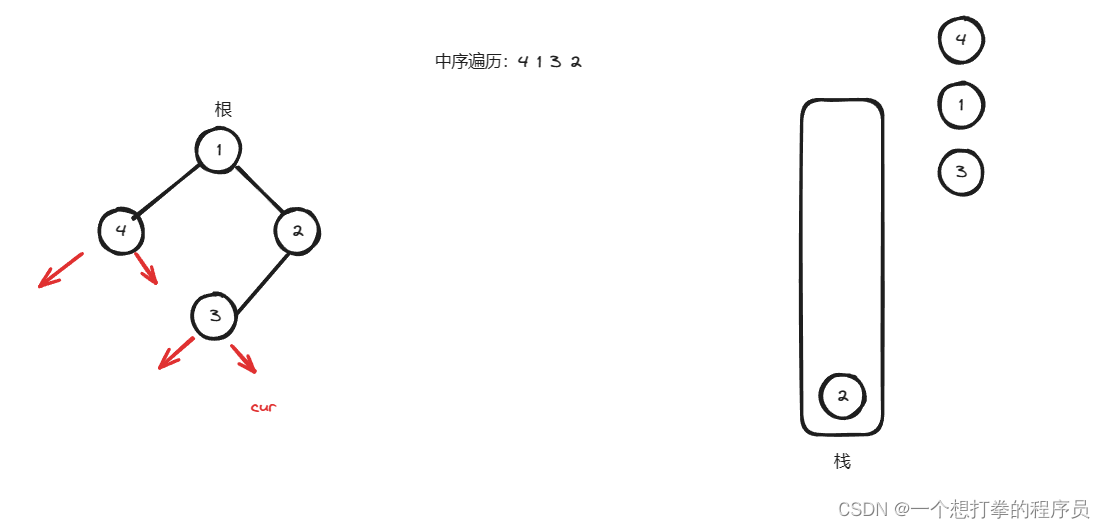
- 根据上图,cur 为空,就要弹出栈顶元素用cur 接收,并且记录到 list 中,得到下图,cur = cur.right
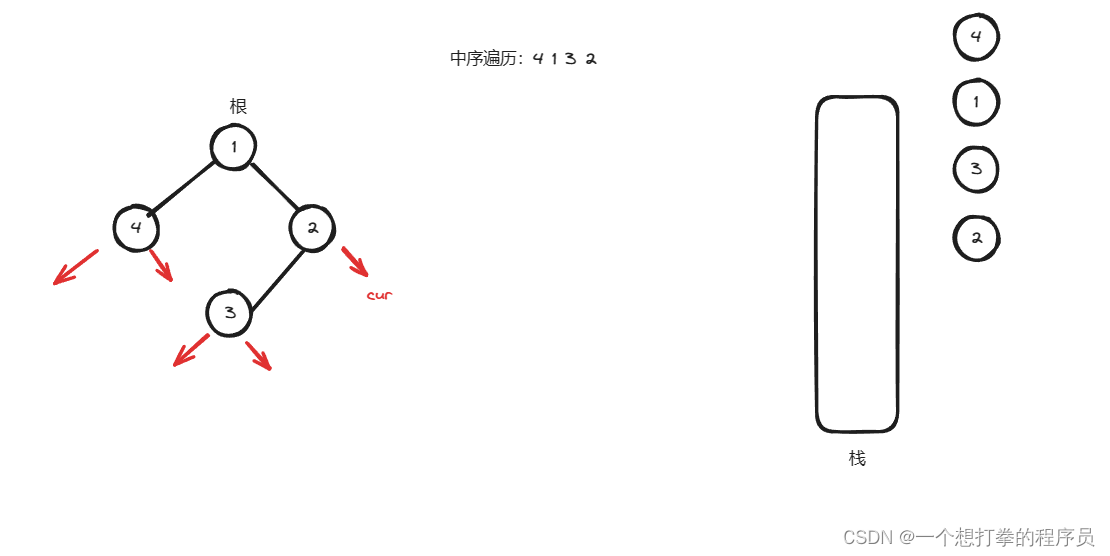
- 此时栈为空,并且 cur == null,就结束了
总结来说:
- cur不为空 一直往左 cur=cur.left ,遇到左元素就入栈,
- cur 为空,就弹出栈顶元素用cur接收,并记录下来,然后 cur = cur.right
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> list = new LinkedList();
Stack<TreeNode> stack = new Stack();
TreeNode cur = root;
while(cur != null || !stack.isEmpty()){
// 一直往左走,找到最左边的元素
if(cur != null){
stack.push(cur);
cur = cur.left;
}else{ // 此时节点为空了
// 弹出最左边元素,此元素就是第一个
cur = stack.pop();
// 放入 list 中
list.add(cur.val);
// 此时开始往右
cur = cur.right;
}
}
return list;
}
}
文章来源:https://blog.csdn.net/hero_jy/article/details/135252840
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 开发需求总结9-el-tree获取选中节点,节点全选时返回被全选子级的父节点,未全选则返回被选中的节点
- 微信如何群发消息?我来教你设置
- MySQL运维实战(2)MySQL用户和权限管理
- 【PostgreSQL】从零开始:(二十)数据类型-日期/时间类型
- pytorch超详细安装教程,Anaconda、PyTorch和PyCharm整套安装流程
- 数据库设计和数据库对象
- SpringBlade export-user SQL 注入漏洞
- Vue 3 父子组件传递数据
- 【linux】用grep或者pgrep查找进程ID
- Go 并查集