蓝桥杯官网题目：2.包子凑数

链接:题目点这里

首先要知道一个数学定理裴蜀定理，还有完全背包的基本运用，这里只介绍前者

也可以看一下我的个人理解，我是第一次听说这个定理，理解可能有误差。

• 假设gcd(a,b)=d,gcd是最大公约数的意思。即a，b的最大公约数是d
• ax+by=m（x，y是任意整数，可正可负）
• 对于所有的m，一定会被d整除，即m%d=0

可以尝试画出ax+by=z的三维立体图，很显然是一个空间平面。

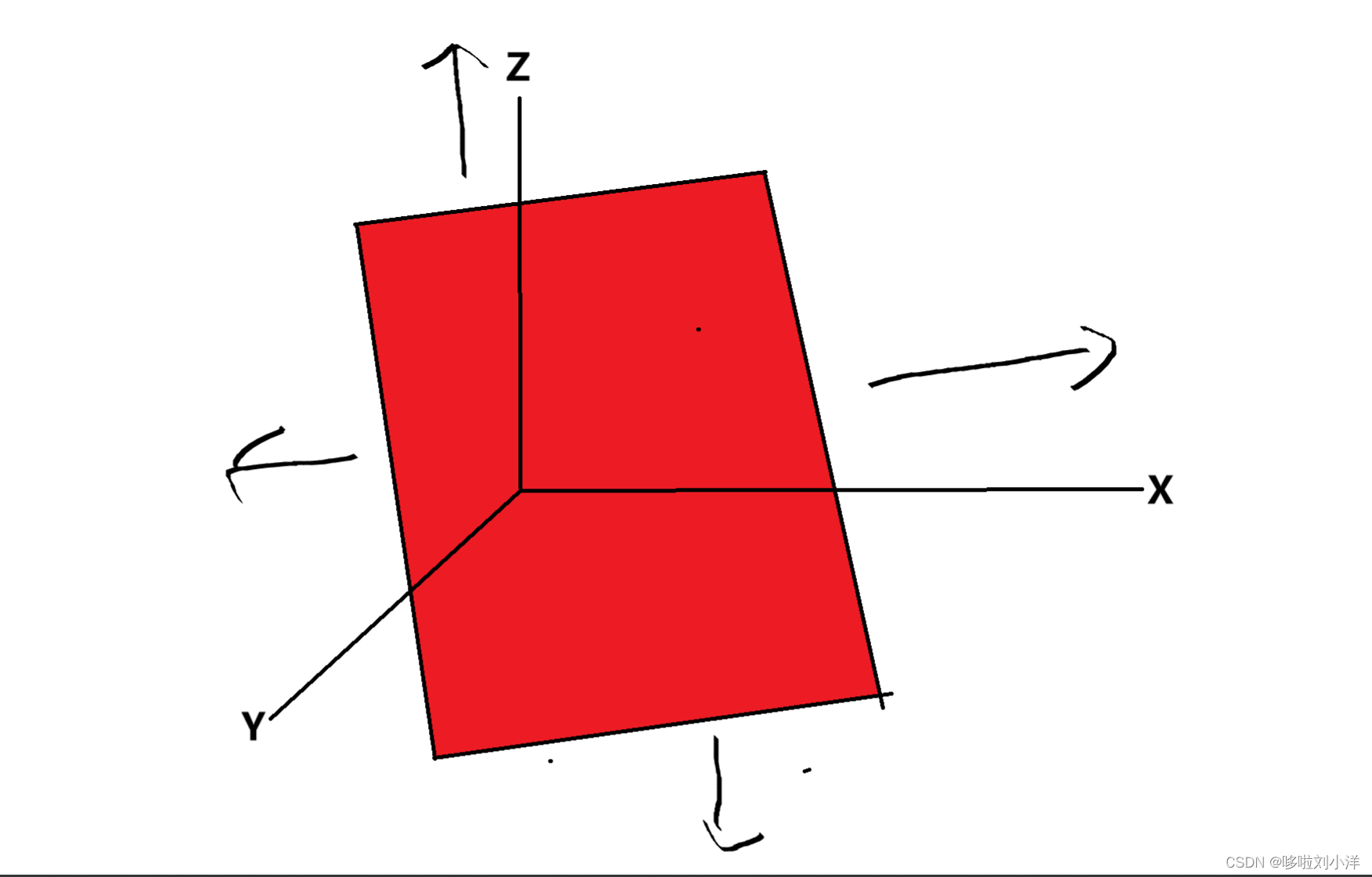
z是一个未知数，它的取值有无数个，如果在三维坐标系中看，那么是所有的z（z可以被gcd（a，b）整除）。
换句话说，ax+by表示的数的集合是{实数中所有的可以被gcd（a，b）整除的数}。

• 以下考虑a，b互质

• a，b如果是互质的，那么
  $$gcd（a，b）=1$$

• 那么ax+by可以构成所有的整数:

  {ax+by | $x\in$N,$y\in$N,$ax+by\in$N}

• 当x，y都是正整数的时候，包括0。ax+by不能表示的最小数是：
  $$(a?1)?(b?1)?1$$

• 也就是说，ax+by可以表示大于(a-1)*(b-1)-1的所有正整数

回到题目
看懂了上面的数学基础应该这个题就比较清晰了。

那我就直接上代码了，不懂的评论区留言

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1e4+1;  //只需要比ax+by的最小值大1就可以了。
const int M = 110;
long long int dp[N];  //dp[i]=j表示取i种包子的方案数是j
//dp[i]=dp[i-a[1]]+dp[i-a[2]]+dp[i-a[3]]+....+dp[i-a[n]]; 
//即，取i种包子的方案数等于取[i-a[1]]包子的方案数+[i-a[2]]包子的方案数+...+[i-a[n]]包子的方案数
int a[M];
int sum = 0;

int gcd(int a, int b)  //辗转相除法
{
    if (a < b)swap(a, b);  //大的数是被除数
    int r = a % b;   //余数
    if (r == 0)return b;
    else
    {
        a = b;
        b = r;
    }
    return gcd(a, b);
}

int main()
{
    int n;
    cin >> n;
    int k;
    for (int i = 1; i <= n; i++)  //找最大公约数
    {
        cin >> a[i];
        if (i == 1)k = a[i];
        else
            k = gcd(k, a[i]);
    }

    if (k != 1)cout << "INF";   //如果最大公约数不是1，那么就会有无穷个数取不到。

    else  //说明最大公约数是1，那么ax+by的值是所有1的倍数，ax+by此时表示整数集（所有整数）
    {
        sort(a + 1, a + n + 1);
        dp[0] = 1;  //取0种包子的方案数是1，即不取，这个必须要有，是很重要的边界初始化
        for (int i = 1; i <= N; i++)  //枚举包子的个数
        {
            for (int j = 1; j <= n; j++)  //然后更新当前包子个数的方案数
            {
                if (i - a[j] < 0)
                    break;
                dp[i] += dp[i - a[j]];
            }
            if (dp[i] == 0)  //退出内嵌for循环判断i个包子的方案数是否是0，如果是，说明这个数不能被构成
                sum++;
        }
        cout << sum << endl;
    }
    return 0;
}

对裴蜀定理有兴趣的可以关注我这篇博客，我会从cf和leetcode等网站更新相关内容，将会以链接形式帖在本篇下面