深度学习中的KL散度

发布时间：2023年12月18日

1 KL散度概述

KL散度（Kullback-Leibler Divergence），也称为相对熵，是信息论中的一个概念，用于衡量两个概率分布间的差异。它起源于统计学家Kullback和Leibler的工作，它的本质是衡量在用一个分布来近似另一个分布时，引入的信息损失或者说误差。在机器学习、深度学习领域中，KL散度被广泛运用于变分自编码器中(Variational AutoEncoder,简称VAE)、EM算法、GAN网络中。

1.1 熵

信息论中，某个信息? $\large x_{i}$ ?出现的不确定性的大小定义为? $\large x_{i}$ ?所携带的信息量，用?I(xi)?表示。I(xi)

与信息? $\large x_{i}$ ?出现的概率? $P(x_{i})$ ?之间的关系为

$I(x_{i}) = \log \frac{1}{P(x_{i})} = -\log P(x_{i})$

例：掷两枚骰子，求点数和为7的信息量

点数和为7的情况为：(1,6) ; (6,1) ; (2,5) ; (5,2) ; (3,4) ; (4,3) 这6种。总的情况为 6*6 = 36 种。

那么该信息出现的概率为? $P_{x=7}=\frac{6}{36}=\frac{1}{6}$

包含的信息量为? $I(7)=-\log P(7)=-\log \frac{1}{6}=\log 6$

以上是求单一信息的信息量。但实际情况中，会要求我们求多个信息的信息量，也就是平均信息量。

假设一共有 n?种信息，每种信息出现的概率情况由以下列出：

$x_{1}$	$x_{2}$	$x_{3}$	$x_{4}$	……	$x_{n}$
$P(x_{1})$	$P(x_{2})$	$P(x_{3})$	$P(x_{4})$	……	$P(x_{n})$

并且有

$\sum_{i=1}^{n}P(x_{i})=1$

则? $x_{1}$ ?,? $x_{2}$ ?, …… ,? $x_{n}$ ?所包含的信息量分别为? $-\log P(x_{1})$ ?,? $-\log P(x_{2})$ ?, …… ,? $-\log P(x_{n})$ 。于是，平均信息量为

$H(x)=-\sum_{i=1}^{n}P(x_{i})\log P(x_{i})$

$H$ 与热力学中的熵的定义类似，故这又被称为信息熵。

例：设有4个信息 A，B，C，D 分别以概率 1/8，1/8，1/4，1/2 传送，每一个信息的出现是相互独立的。则其平均信息量为：

$H(x)=-(\frac{1}{8}\log( \frac{1}{8}) +\frac{1}{8}\log( \frac{1}{8})+\frac{1}{4}\log( \frac{1}{4}) +\frac{1}{2}\log( \frac{1}{2}))=1.75$

连续信息的平均信息量可定义为

$H(x)=-\int_{}^{}f(x)\log f(x)dx$

这里的? $f(x)$ ?是信息的概率密度。

上述我们提到了信息论中的信息熵

$H(x)=-\sum_{i=1}^{n}P(x_{i})\log P(x_{i})=\sum_{i=1}^{n}P(x_{i})\log \frac{1}{P(x_{i})}=H(P)$

这是一个平均信息量，又可以解释为：用基于P的编码去编码来自P的样本，其最优编码平均所需要的比特个数。

接下来我们再提一个概念：交叉熵

$H(P,Q)=-\sum_{i=1}^{n}P(x_{i})\log Q(x_{i})=\sum_{i=1}^{n}P(x_{i})\log \frac{1}{Q(x_{i})}$

这就解释为：用基于P的编码去编码来自Q的样本，所需要的比特个数。

【注】 $P(x)$ ?为各字符出现的频率， $\log \frac{1}{P(x)}$ ?为该字符相应的编码长度， $\log \frac{1}{Q(x)}$ 为对应于Q的分布各字符编码长度。

1.2 KL散度

KL散度又可称为相对熵，描述两个概率分布 P 和 Q 的差异或相似性，用 $D_{KL}\left ( P\left | \right | Q\right )$ 表示

$D_{KL}(P\left | \right |Q)=H(P,Q)-H(P)$

? ? ? ? ? ? ? ? ? ? ?? $=\sum_{i}^{}P(x_{i})\log \frac{1}{Q(x_{i})}-\sum_{i}^{}P(x_{i})\log \frac{1}{P(x_{i})}$

? ? ? ? ? ? ? ? ? ? ?? $=\sum_{i}^{}P(x_{i})\log \frac{P(x_{i})}{Q(x_{i})}$

当 $P,Q$ 为连续变量的时候，KL散度的定义为:

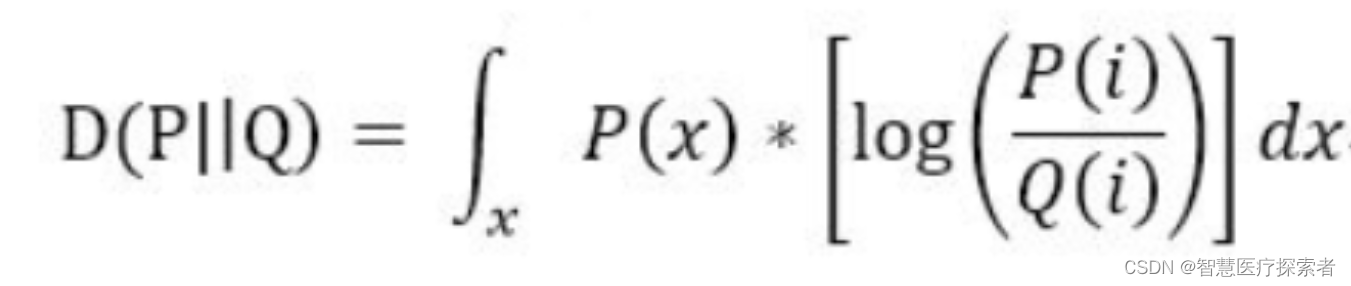
散度越小，说明概率 Q 与概率 P 之间越接近，那么估计的概率分布与真实的概率分布也就越接近。

KL散度的性质：

非对称性： $D_{KL}(P\left | \right |Q)\neq D_{KL}(Q\left | \right |P)$
$D_{KL}(P\left | \right |Q)\geqslant 0$ ，仅在? $P=Q$ ?时等于0

1.3 前向KL散度与反向KL散度

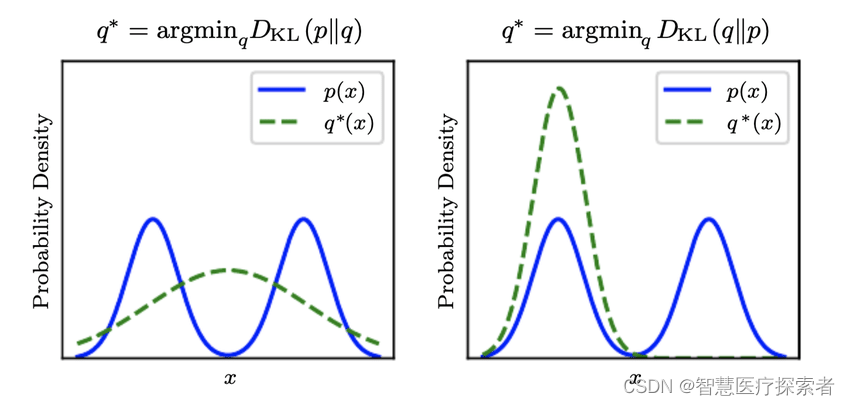
假设某优化问题中, P(X)是真实分布（true distribution），Q(X)是一个用于拟合P(X)的近似分布（approximate distribution），我们尝试通过修改Q(X)使得二者间的 $KL\left [ P(X)\left | \right |Q(X) \right ]$ 尽可能小来实现用Q(X)拟合P(X)，如下图所示

在上面的概率拟合应用场景下， $KL\left [ P(X)\left | \right |Q(X) \right ]$ 被称为前向KL散度（forward Kullback-Leibler Divergence），将 $KL\left [ Q(X)\left | \right |P(X) \right ]$ 称为反向KL散度（reverse Kullback-Leibler Divergence）。

这里需要注意的是，只有在概率拟合的应用场景下（也就是确定了真实分布和拟合分布两个角色之后），前向KL散度 $KL\left [ P(X)\left | \right |Q(X) \right ]$ 和反向KL散度 $KL\left [ Q(X)\left | \right |P(X) \right ]$ 的定义才是有意义的，否则二者只是相同公式改变正负号、并交换P和Q符号表示之后的平凡结果。

1.4 两类KL散度拟合效果的定性分析

极小化前向KL代价下的拟合行为特性：寻找均值（Mean-Seeking Behaviour）

前向KL的计算式中， $P\left ( x \right )$ 和 $Q\left ( x \right )$ 在每个样本点上的差异程度被 $P\left ( x \right )$ 加权平均，我们基于此对前向KL的特性进行分析。

考虑随机变量 $X$ 的子集 $X_{0}=\left \{ x|P(x)=0 \right \}$ ，由于 $P\left ( x \right )$ 是前向KL公式中的权重系数，因此 $X_{0}$ 中的元素实际上对前向KL的值没有任何影响。换言之，对任意 $x\epsilon X_{0}$ ，无论 $P\left ( x_{0} \right )$ 与 $Q\left ( x_{0} \right )$ 相差多大都对前向KL的计算结果毫无影响，因此前向KL值不受 $Q\left ( x \right )$ 在子集 $\left \{ x|P(x)=0 \right \}$ 上取值的影响。在极小化前向KL散度的过程中，每当 $P\left ( x \right )=0$ ， $Q\left ( x \right )$ 就会被无视。从连续性角度推理，最小化前向KL散度倾向于忽视" $Q\left ( x \right )$ 在满足 $P\left ( x \right )$ 近似为 0 的随机变量取值集合上的拟合精度”，而去更努力的实现“ $Q\left ( x \right )$ 在满足 $P\left ( x \right )>0$ 的随机变量取值集合上的拟合精度”。上述分析结论总结如下：

Wherever P ( ? ) P(·) P(?) has high probability, Q ( ? ) Q(·) Q(?) must also have high probability.

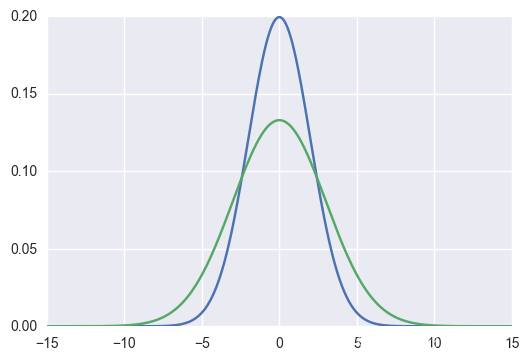
下图展示了使用前向KL散度代价拟合一个多峰（实际上是双峰）分布的效果示意图。

图中绿色曲线代表拟合分布Q，蓝色曲线是目标分布P

前向KL散度的这种特性一般也被称为 zero avoiding，原因是它倾向于避免在任何 $P\left ( x \right )>0$ 的位置 $X$ 使得 $Q\left ( x \right )=0$ 。

极小化反向KL代价下的拟合行为特性：搜寻模态（Mode-Seeking Behaviour）

在反向KL中，差异加权求和时的权重系数是 $Q\left ( x \right )$ 。此时， $P\left ( x \right )$ 在子集 $\left \{ x|Q(x)=0 \right \}$ 的取值不影响反向KL值的计算，而当 $Q\left ( x \right )>0$ 时， $Q\left ( x \right )$ 与 $P\left ( x \right )$ 的差异需要尽可能小以使得反向KL值尽可能小。上述分析结论总结如下：

Wherever Q ( ? ) Q(·) Q(?) has high probability, P ( ? ) P(·) P(?) must also have high probability.

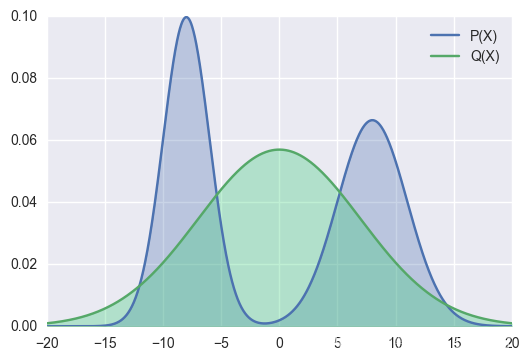
下图展示了使用前向反向KL散度代价拟合一个多峰（实际是双峰）分布的效果示意图。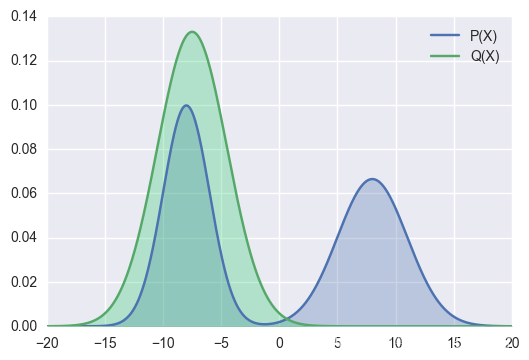

图中绿色曲线代表拟合分布Q，蓝色曲线是目标分布P

关于在前向KL拟合特性分析中，为什么说当 $P\left ( x \right )$ 近似为 0 时，无论 $Q\left ( x \right )$ 的取值如何（即使绝对值非常大）,一般都不会对前向KL散度计算产生影响的原因定性的论述如下。

首先，如果当 $P\left ( x \right )\rightarrow 0$ 时， $Q\left ( x \right )$ 并不趋近于0，用数学语言可以描述为：存在一个 $\varepsilon >0$ , 有 $Q\left ( x \right )>\varepsilon$ 。那么这时一定有

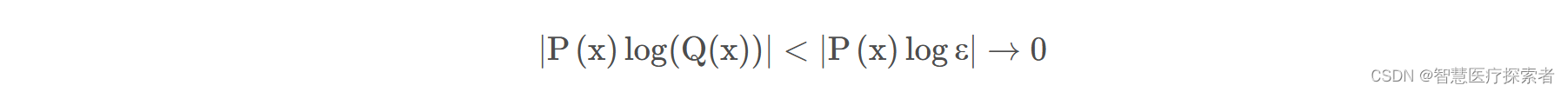
这说明，当概率分布 $Q\left ( x \right )$ 有下大于0的下界（注意：由于 $Q$ 是概率分布，所以 $Q\left ( x \right )$ 取值本就一定在 [0 , 1] 上）时， $P\left ( x \right )log\left ( Q(x) \right )$ 在 $P\left ( x \right )$ 近似为0时实际可忽略的。

其次，考虑如果 $Q\left ( x \right )$ 也趋向于０，也就是 $log(Q(x))\rightarrow \infty$ 时， $P(x)log(Q(x))$ 的极限是否还是0？具体是如下问题：假设当 $P\rightarrow 0$ 时，也有 $Q\rightarrow 0$ ，且二者趋于0的“速度”是相近的，求 $P(x)log(Q(x))$ 的极限。不妨将该问题按如下方法求解：

上面的定性证明过程中的第一个等号左边的表达式，其实也可以使用洛必达法则（L’Hospital’s rule）求解。该证明的意义在于说明：若 $PlogQ$ 中的 $P$ 和 $Q$ 以近似相同的速度趋向于0，则 $PlogQ$ 也会趋向于0。这背后隐含的意义是：只要 $P\left ( x \right )$ 在 $x$ 处接近于0，那么 $Q\left ( x \right )$ 无论取何值（这里的“无论”是指 $Q$ 有大于0的下界或至多是 $P$ 的等价无穷小量），那么 $P(x)log(Q(x))$ 就是可忽略的。这也就定性的证明，在拟合中 $Q$ 在 $P(x)$ 中接近于0的那部分自变量集合上花费精力基本是无意义的，因此拟合结果 $Q$ 会表现为倾向于拟合 $P>0$ 的那些区域。

其他示例

前向KL和反向KL拟合效果的二维多峰（实际上是双峰 $P$ ）分布情况示例：

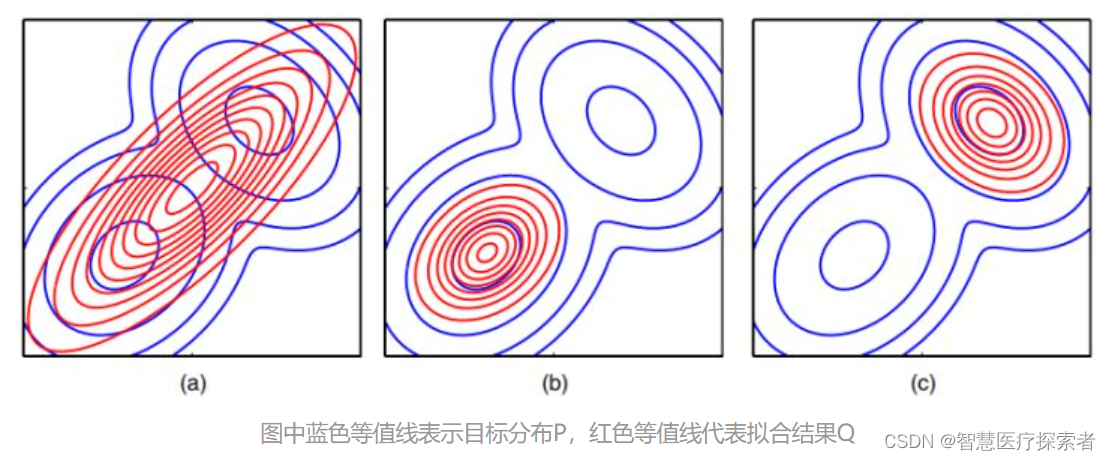
上面图中蓝色的轮廓线代表一个有两个高斯分布组成双峰分布 $P\left ( x \right )$ ，红色的轮廓线是使用单一高斯分布在最小化KL散度意义下对 $P\left ( x \right )$ 进行拟合得到的最佳结果。其中图(a)是拟合代价选择前向KL散度时的拟合效果，图(b)时拟合代价选择反向KL散度 $KL(P\left | \right |Q)$ 时的拟合效果，图(c)和图(b)使用相同的代价但展示的是到达反向KL散度代价的另外一个局部极小值点的效果。

1.5 两类KL散度拟合效果的数学推导

2 KL散度计算

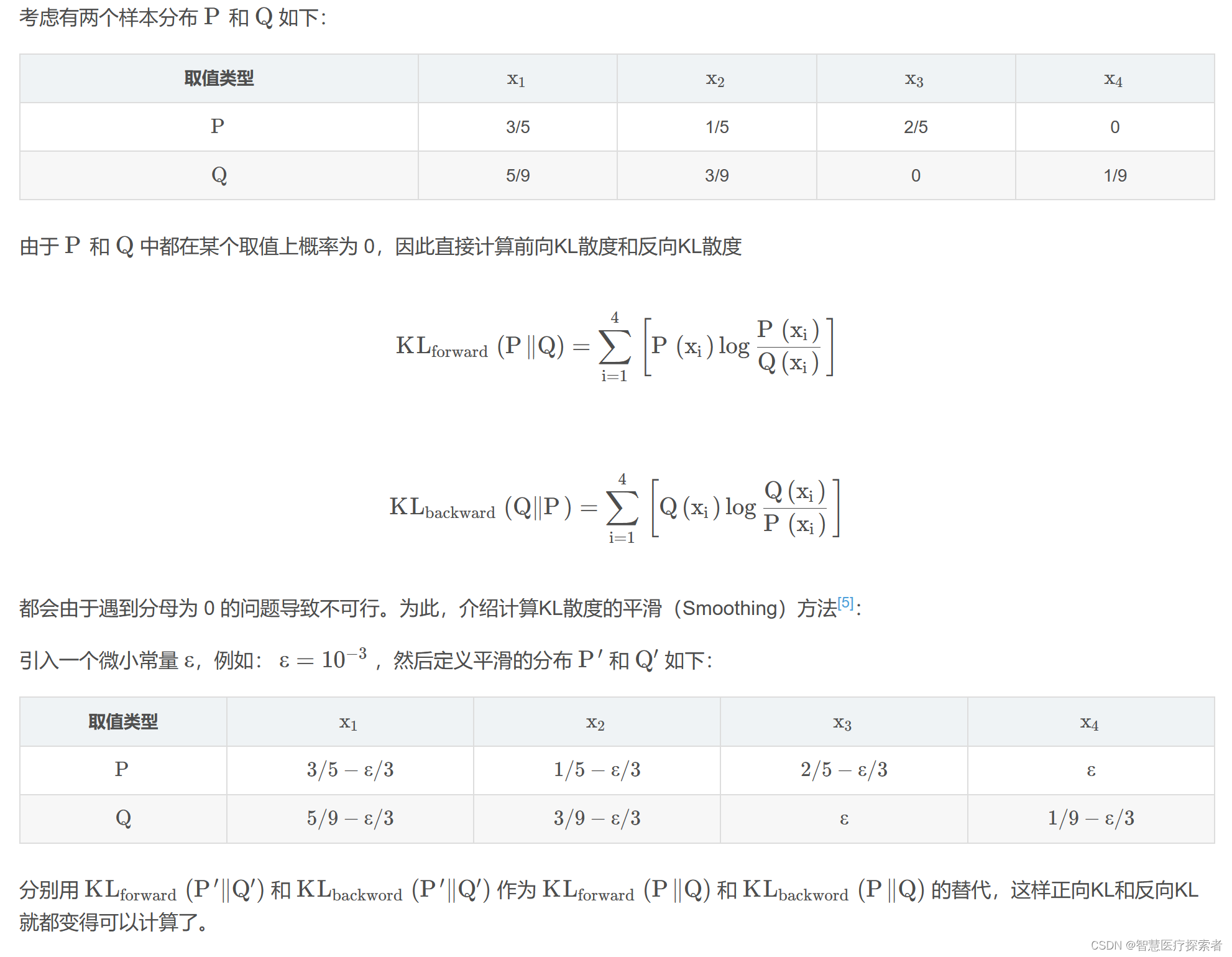
3 KL散度的代码实现

import numpy as np
import math


def kld_softmax(x, y):
    px = get_gauss_dist(x, 1, 0.2)
    py = get_gauss_dist(y, 2, 0.5)

    softmax_x = softmax(px)
    softmax_y = softmax(py)

    KL = 0.0
    for i in range(len(softmax_x)):
        KL += softmax_x[i] * np.log(softmax_x[i] / softmax_y[i])
    return KL


def kld_smooth(x, y):
    px = get_gauss_dist(x, 1, 0.2)
    py = get_gauss_dist(y, 2, 0.5)

    # smoothing
    px += 0.001 / 3
    py += 0.001 / 3

    KL = 0.0
    for i in range(len(px)):
        KL += px[i] * np.log(px[i] / py[i])
    return KL


def softmax(x, t=1):
    # 计算每行的最大值
    row_max = x.max()

    # 每行元素都需要减去对应的最大值，否则求exp(x)会溢出，导致inf情况
    row_max = row_max.reshape(-1, 1)
    x = x - row_max

    # 计算e的指数次幂
    x_exp = np.exp(x / t)
    x_sum = np.sum(x_exp, keepdims=True)
    s = x_exp / x_sum
    return s


def get_gauss_dist(x, mu=0, sigma=1):
    left = 1 / (np.sqrt(2 * math.pi) * np.sqrt(sigma))
    right = np.exp(-(x - mu) ** 2 / (2 * sigma))
    return left * right


x = np.arange(-4, 5, 0.1)
y = np.arange(-3, 6, 0.1)
print("kld_softmax:", kld_softmax(x, y))
print("kld_smooth:", kld_smooth(x, y))

运行代码显示：

kld_softmax: [-0.00016308 -0.00016308 -0.00016308 -0.00016308 -0.00016308 -0.00016308
 -0.00016308 -0.00016308 -0.00016308 -0.00016308 -0.00016308 -0.00016309
 -0.00016309 -0.00016309 -0.0001631  -0.00016311 -0.00016314 -0.00016319
 -0.00016328 -0.00016345 -0.00016375 -0.00016429 -0.00016522 -0.00016678
 -0.00016937 -0.00017355 -0.00018016 -0.0001904  -0.00020589 -0.00022883
 -0.00026198 -0.00030871 -0.00037285 -0.00045836 -0.00056868 -0.0007057
 -0.00086847 -0.00105147 -0.001243   -0.00142352 -0.00156396 -0.00162337
 -0.00154552 -0.00125551 -0.0006615   0.00032705  0.00175073  0.00351986
  0.00534313  0.00675284  0.00728793  0.00675284  0.00534313  0.00351986
  0.00175073  0.00032705 -0.0006615  -0.00125551 -0.00154552 -0.00162337
 -0.00156396 -0.00142352 -0.001243   -0.00105147 -0.00086847 -0.0007057
 -0.00056868 -0.00045836 -0.00037285 -0.00030871 -0.00026198 -0.00022883
 -0.00020589 -0.0001904  -0.00018016 -0.00017355 -0.00016937 -0.00016678
 -0.00016522 -0.00016429 -0.00016375 -0.00016345 -0.00016328 -0.00016319
 -0.00016314 -0.00016311 -0.0001631  -0.00016309 -0.00016309 -0.00016309]
kld_smooth: 1.5577555319530605

4 总结

KL散度是衡量两个概率分布差异的一个重要工具。它在信息论、机器学习和统计学中有着广泛的应用。其非对称性和零不容忍特性使其在实际应用中需谨慎处理。通过KL散度，我们可以量化不同概率分布间的差异，从而在多种应用场景中发挥重要作用。

文章来源:https://blog.csdn.net/lsb2002/article/details/135059288
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！