前缀和详解，朴素前缀和，前缀和变形，二维前缀和

一、朴素前缀和

1、部分和

所谓部分和，就是给定一个数组, 求它的某一段连续子数组的和。

2、朴素做法

比较传统的做法，就是对于要求部分和的区间**[l ， r]**，枚举所有的数进行相加，如下:

int partialSum(int* a , int l , int r)
{
    int i;
    int s = 0;
    for(i = l ; i <= r ; i++)
        s += a[i];
    return s;
}

函数的返回值代表了求a[] 数组的第|项到第r项的和，如果数组长度为n,这样做的最坏时间复杂度为O(n)。那么,试想一下，如果有m次询问，每次询问都是O(n),时间复杂度就会变成0(nm),有没有办法优化呢?

3、前缀和

我们可以用一个sum[数组来表示数组的前缀和，即sum[i]示的是前i项的和，数学公式
如下:

于是可以得到

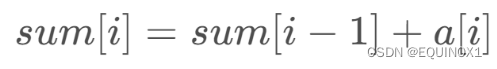
4、前缀和的边界值

有了递推式，我们还需要有一个边界值,从定义出发,边界值应该是:

怎么理解呢?试想一下，sum[1] 表示的是从第0项到第项; sum[0] 示的是从第0项累到第项; sum[-1] 表示的是一项都没有累加，那么这个值自然就是零了。即:

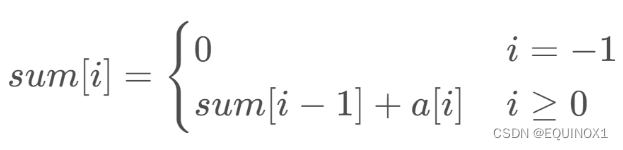
5、边界处理

这时候，我们需要注意C/C++中的下标是从零开始的，所以，sum[-1] 会导致数组下标越界，可以将它转换成函数的形式将数组sum[]进行一次封装:

int prefixSum(int n)
{
    if(n == -1)
        return 0;
    return sum[n];
}

6、再看部分和

然后，我们继续来看部分和,有了前缀和数组sum[以后,我们就可以利用差分法,在0(1)的时间内求得部分和，原因就是:

于是，只要预先将前缀和全部求出来，面每次询问都可以做到(1)了。

二、前缀和变形

1、前缀积

顾名思义，我们可以用一个prod[]数组来表示数组的前缀积，即prod[i]示的是前i项的积，数学公式如下:

将i-1代入上述的i,得到:

于是可以得到:

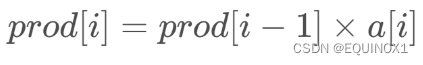
2、前缀异或和

同样，还有前缀异或和，同样满足这个性质，如下:

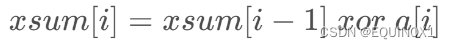
三、二维前缀和

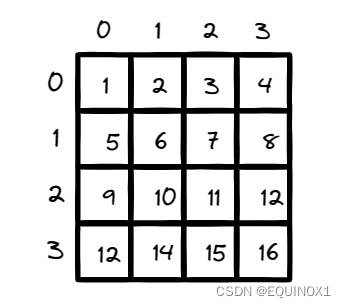
对于这样一个矩阵，我们是否可以仿照一维前缀和那样求出二维前缀和从而快速求出任意子矩阵的和？

答案是可以。

定义sum[i+ 1][j+ 1]表示左上角为grid[0][0]，右下角为grid[i][j] 的子矩阵元素和。采用这种定义方式，无需单独处理第一行第一 列的元素和。
$$sum[i+1][j+1]=sum[i+1][j]+sum[i][j+1]?sum[i][j]+grid[i][j].$$
那么这个递推公式的含义是什么呢？

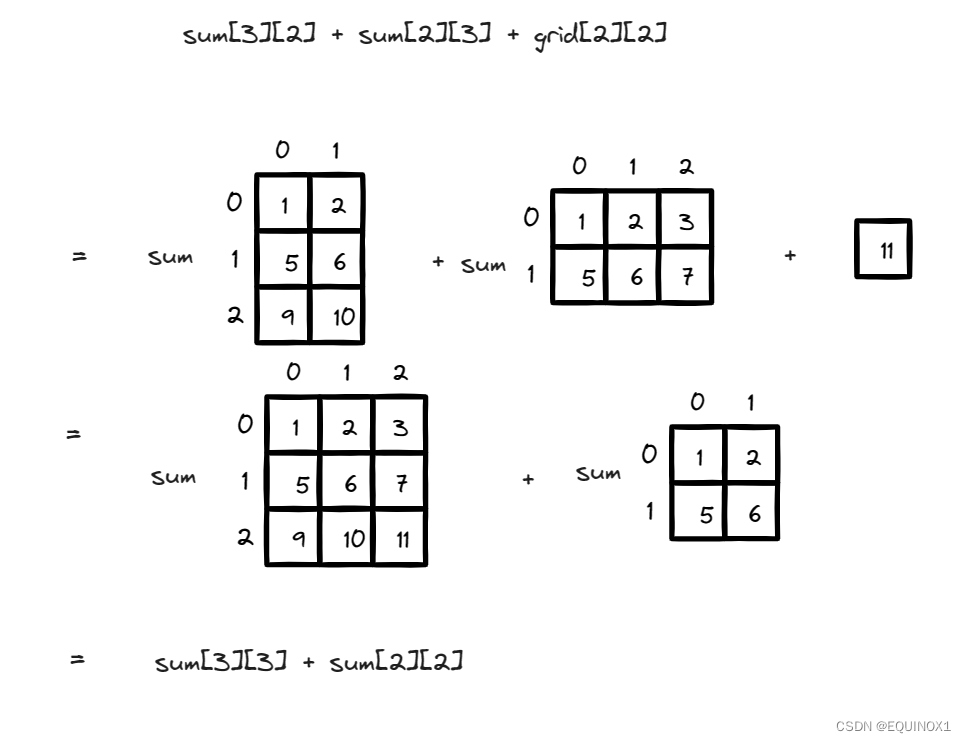
所以我们子矩阵的前缀和是由两个小矩阵减去重叠部分再加上一个格子得到的

二位前缀和代码实现

	MatrixSum(vector<vector<int>> &grid) {
        int m = grid.size(), n = grid[0].size();
        sum = vector<vector<int>>(m + 1, vector<int>(n + 1));
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                sum[i + 1][j + 1] = sum[i + 1][j] + sum[i][j + 1] - sum[i][j] + grid[i][j];
            }
        }
    }
    // 返回左上角在 (r1,c1) 右下角在 (r2,c2) 的子矩阵元素和
    int query(int r1, int c1, int r2, int c2) {
        return sum[r2 + 1][c2 + 1] - sum[r2 + 1][c1] - sum[r1][c2 + 1] + sum[r1][c1];
    }