线段树简单板子+介绍
线段树:
什么是线段树?
先用一个问题来引出线段树的论述:
给你一段区间,然后给你 q次询问,每次询问让你输出这个区间的最大值。
乍一看,这不是很简单吗?只需要这样这样再那样那样就好了。
nonono
如果q=1e6次呢? 那么这就暗示你需要一个O(1)的算法来解决这道题目。
而线段树就是解决这一类问题的好方法。
那么回来了,线段树是什么? 我们只知道线段树是一种数据结构,它能处理上面的问题。还有么?
其实,线段树的用途很广泛,他能作用大多数的区间查询问题。
例如求区间和、求区间最值、求区间内满足某种条件的元素个数等等。
你可能已经迫不及待地想要学习线段树了。
我们先抛开线段树这三个字。对于上面的问题,我们可以这样思考:
由于询问次数高达1e6次方,所以必须使用O(1)的算法。
这也就意味着,我们必须对这个问题进行预处理。只有这样我们才能在每次询问的时候直接得到答案。
假设num[l][r] 表示的是这个区间里的最大值
单在这个区间较长的情况下,我们无法将答案预处理到一个二维数组里面
因为空间复杂度将爆炸。
所以我们可以构建一个函数,这个函数的参数有我们需要查询的左右两个端点。返回值就是这个区间的最大值。
然后每次调用函数能以非常短的次数得到答案。
ok,现在的问题就是,怎么用很低的时间复杂度找到某一区间内的最大值呢?
对,没错就是二分。
一个区间的最大值,取决于? ?这个区间左半边的最大值,和区间右半边的最大值
然后一直递归下去,直到边界,也就是这个区间长度为1.
因为: “每一个单位长度为1的区间,其最大值就是本身。”
递归到边界之后,直接返回边界值,然后根据刚刚说的:
“ 这个区间的最大值,取决于? ?这个区间左半边的最大值,和区间右半边的最大值 ”
最后将每个区间的最大值存入一个数组。。。。
于是。。。
神乎其技!? ?我们有了这整个线段的最大值。
其实我们仔细看看这个思路,会发现,哎哟我去,这不是分治吗。或者是:哎哟我去,这不是二叉树吗。
是的,于是我们可以用二叉树来完成上面的操作:
- 首先构建一颗二叉树,二叉树的每个结点表示一段区间。而叶子结点就表示一个个长度是1的区间,再上一层就是长度为2的区间。。。以此类推(类似这样)
[1,8] (最大值: 8)
/ \
[1,4] [5,8]
(最大值: 4) (最大值: 8)
/ \ / \
[1,2] [3,4] [5,6] [7,8]
(2) (4) (6) (8)
- 然后写一个查询函数,search(当前结点编号,当前结点编号对应区间,需要查询的区间)
这就是经典的二分了,查询这个区间是在哪个结点处,如果这个区间能把当前结点对应的区间包含住,那么我们直接返回这个结点的值就可以了。
否则的话,根据这个区间出现在左半边还是右半边进行二分查找即可
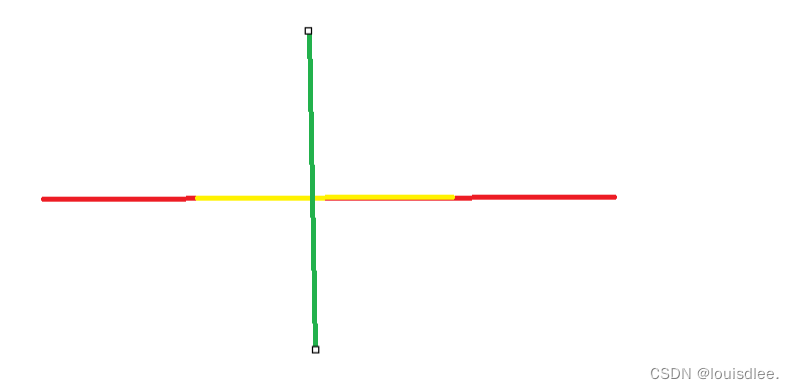
(有人可能会问,如果这个区间,出现在结点区间的中间怎么办)
(ps:黄色是目标区间,红色是当前结点区间,绿色是二分的位置。)
难办?其实是一样的,如果在中间的话,我们还是能继续二分啊,
只不过我们继续二分的话,会分别二分到黄色区间的左端点,和右端点。
当结点区间的左端点为目标区间的左端点的时候(结点区间的右端点是绿色处)
那么我们不就求出了左黄部分的最大值了吗。
右端点同理啊。
而一个区间的最大值不就是可以分为这个区间以某点为分界线的左边最大值和右边最大值的最大值吗?
所以就求完了啊。
而第三种情况就是,当你的目标区间和结点区间完全没有交集的时候,我们直接返回0就可以了。
? ? ? ?
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<cstring>
#include<string>
#include<algorithm>
#include<vector>
#include<cctype>
#include<map>
#include<set>
#include<queue>
#include<numeric>
#include<iomanip>
#include<stack>
#include<list>
using namespace std;
const int N = 1e6 + 7;
int a[N];//已知区间
int tree[4 * N];//用来存储树的信息
//建立线段树
//可以用二叉树来构建,二叉树的左右子节点分别是2n,2n+1
void build_segment_tree(int root,int l,int r) {
if (l == r) { //如果区间长度是1,那么该结点时叶子结点,存放的是区间[l,l]的最大值
tree[root] = a[l];
return;
}
int mid = (l + r) >> 1; //不断二分将整个区间都拆分到这棵树里
build_segment_tree(root * 2, l, mid); //构建左子树
build_segment_tree(root * 2 + 1, mid + 1, r);//构建右子树
tree[root] = max(tree[root * 2], tree[root * 2 + 1]);//父节点取两个子结点中的最大值
}
int search_max(int root, int l, int r, int ql, int qr) { //查询[ql,qr]最大值
if (ql <= l and qr >= r) { //如果[ql,qr] 将 [l,r] 包裹,那么直接返回结点信息。其实l,r两端中的某一端已经与ql,qr重合了,所以可以直接返回。
return tree[root];
}
if (ql > r or qr < l) { //如果完全没有交集,那么就不需要继续二分下去,直接返回一个非法的值
return 0;
}
//二分
int mid = (l + r) >> 1;
int left=search_max(root * 2, l, mid, ql, qr);
int right=search_max(root * 2 + 1, mid + 1, r, ql, qr);
return max(left, right);//一段区间的最大值,一定是左区间和右区间的最大值。
}
/*void update(int root, int l, int r, int pos, int val) { //更新pos点的值为val
if (l == r) {
tree[root] = val;
return;
}
int mid = (l + r) >> 1;
if (pos <= mid) {
update(root * 2, l, mid, pos, val);
}
else {
update(root * 2 + 1, mid + 1, r, pos, val);
}
tree[root] = max(tree[root * 2 + 1], tree[root * 2]);
}*/
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; i++)cin >> a[i];
build_segment_tree(1, 1, n); //根节点是1,左端点是1,右端点是n
int q;
cin >> q;
while (q--) {
int l, r;
cin >> l >> r;
cout << search_max(1, 1, n, l, r)<<endl;
}
}
总结一下线段树:
- 线段树是一种用于高效处理区间查询的数据结构,通常用于解决数组或线性数据结构上的区间查询问题。
- 线段树的基本思想是将一个线性的区间划分成若干个小区间,对每个小区间维护一个值,然后通过递归的方式建立一棵树状结构,使得每个节点代表一个区间,并且这些区间两两不重叠,同时完全覆盖整个线性区间。这样,就可以在每个节点上记录该区间的一些信息,比如最大值、最小值、区间和等等,以便快速地进行区间查询和更新操作。
- 线段树的建立过程和查询过程都是基于递归的思想,可以利用二叉树的结构来表示。对于一个线性区间 [l, r],可以将其划分为 [l, m] 和 [m+1, r] 两个子区间,然后分别递归地构建左右子树,直到区间长度为1时停止递归。线段树的查询操作也是通过递归地向下搜索树的节点,并结合区间的位置关系和需要的信息进行计算得出结果。
- 线段树在解决一些区间查询问题上有着良好的效果,比如求区间最大值、最小值、区间和、区间内满足某种条件的元素个数等。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 第十六章 i18n国际化
- 【算法题】3. 无重复字符的最长子串
- win10 openvpn搭建与安卓客户端使用
- 6、docker 安装mysql8
- 湖农大邀请赛shell_rce漏洞复现
- 医院信息系统集成平台—后台运维管理系统
- Doris数据库误删除恢复
- 【shell编程入门】stable diffusion webui的webui.sh脚本解析
- CG Magic分享3d max渲染效果图时,不可忽略的灯光技巧!
- 【方案】如何利用大数据+云计算技术打造智能环境监控系统?