【算法】利用双指针解决算法题（C++）

1. 前言

1. 双指针并非真正意义上的指针，实际上一般使用下标表示/代替。
2. 通常用于处理数组或链表等数据结构。
3. 主要思想是使用两个指针在数组或链表中进行迭代、比较或操作

2. 双指针法引入

我们直接通过下面一道例题进行双指针方法的引入

283.移动零

思路

1. 如图所示，我们定义双指针，每次移动指针，数组都满足：
   • cur左侧元素为处理过的元素，右侧为未处理的元素
   • 处理后的元素分为非零元素和零
   • dest 左侧为非零元素，dest与cur之间为零
2. 细节注意：
   • 由于cur从0开始遍历数组，将dest从-1位置开始
   • 如果cur当前元素不为0，则于dest位置元素交换（先进行++dest）

代码

void moveZeroes(vector<int>& nums) {
    // cur: 从左到右遍历数组，dest: 非零元素的最后一个位置
    // [0, dest] 非零 [dest+1, cur-1] 零 [cur+1, n-1] 未处理
    int cur = 0, dest = -1;
    for(cur = 0; cur < nums.size(); ++cur)
    {
        if(nums[cur] != 0)
            std::swap(nums[++dest], nums[cur]);
    }
}

---

3. 使用双指针法解决算法题

1089.复写零

思路

1. 题目要求复写数组中的0，且数组长度不变（且应就地修改数组）
2. 此时我们思考：
   • 当从前向后复写的时候，如1023 -> 1002，此时就会发生问题，当我们将0复写到2的位置后，2已经被覆盖，后续找不到该元素了
   • 此时我们可以尝试进行从后向前复写
3. 当决定从后向前复写的操作，此时思路步骤如下图所示：
   

代码

void duplicateZeros(vector<int>& arr) {
    int cur = 0, dest = -1;
    int n = arr.size();
    // 先找到最后一个复写的数
    while(dest < n - 1)
    {
        // num[cur] 不为0，cur，dest后移一步，为零cur后移一步dest后移两步
        if(arr[cur] != 0)  dest++;
        else    dest += 2;

        if(dest >= n-1) break;
        cur++;
    }

    // 处理边界情况 如[1, 0, 2, 3, 0, 4]
    if(dest == n)
    {
        arr[n-1] = 0;
        dest-=2, cur--;
    }

    // 从后向前复写
    while(cur >= 0)
    {
        if(arr[cur] != 0)
        {
            arr[dest--] = arr[cur];
        }
        else
        {   // nums[cur] 为零，复写两次
            arr[dest--] = 0;
            arr[dest--] = 0;
        }
        cur--;
    }
}

---

202.快乐数

思路

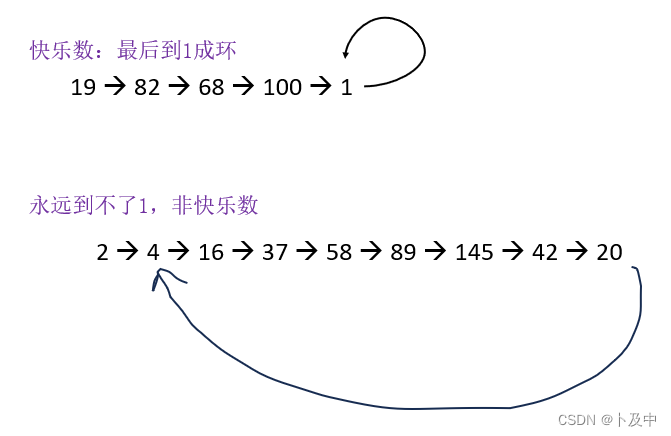
1. 我们首先通过上面的方式有了判断快乐数的方法，即一直算平方和看最后成环是否有1
2. 对于此类成环问题，如判断链表是否有环，我们采用快慢指针来解决：
   • 如果快慢指针相遇，如果相遇位置不等于1，则不是快乐数
3. 由此我们可以编写代码↓

代码

• 将求 每位平方和 的操作写位函数
• 快慢指针的移动，即求每位平方和的次数：
  • 慢指针每次求一次，快指针每次求两次。
  • 当两指针相遇，通过判断某个指针是否为1返回最终结果。

// 求每位平方和
int bitSquare(int n)
{
    int sum = 0; 
    while(n > 0)
    {
        int bit = n % 10;
        sum += bit * bit;
        n /= 10;
    }
    return sum;
}

bool isHappy(int n) {
    // 由已知得，数字一定成环，当slow与fast相遇
    // 如果相遇位置值为1，则是快乐数
    int slow = n, fast = bitSquare(n);;
    while(slow != fast)
    {
        // 慢指针每次一步，快指针每次两步
        slow = bitSquare(slow);
        fast = bitSquare(bitSquare(fast));
    }

    return fast == 1;
}

---

11.盛最多水的容器

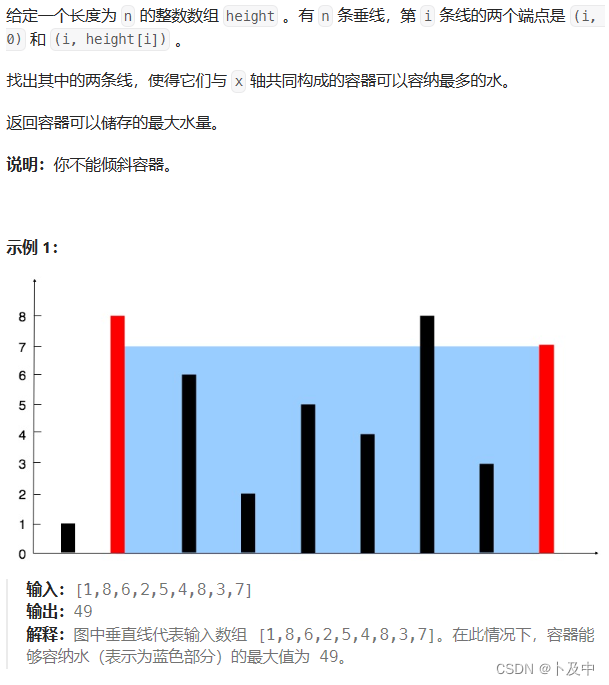
思路

• 解法一：暴力解法：

  

• 解法二：利用单调性，使用双指针法

  

• 有了双指针法的前提算法思想，我们可以总结出步骤：

  • 每次统计以left，right为边界的容量，并移动值更小的指针，重复步骤直到指针相遇

代码

int maxArea(vector<int>& height) {
   int left = 0, right = height.size() - 1, ret = 0;
    
    while(left < right)
    {
        // 算出本次体积
        int v = min(height[left], height[right]) * (right - left);
        ret = max(ret, v);
        
        // 调整指针
        if(height[left] > height[right]){
            right--;
        }
        else{
            left++;
        }
    }
    
    return ret;
}

---

611.有效三角 形的个数

思路

• 解法一：暴力枚举
  • 用三个for循环计算更新结果，时间开销太大！

for(int i = 0; i < n-1; ++i)
	for(int j = i + 1; j < n - 1; ++j)
		for(int k = j + 1; k < n - 1; ++k)
			check(i, j, k); // 省略具体步骤

• 解法二：根据单调性用双指针法

  1. 我们知道三条边构成三角形的条件是 任意两条边之和>第三条边
  • 而对于a <= b <= c 的三条边来说，由于a+c > b, b + c > a恒成立，我们只需判断a + b > c 是否成立即可 （注意下图思路中，我们用下标表示其在数组中的值）

  
  2. 则思路如下：

  • 排序数组
  • 通过外层for循环固定最大边，内层while循环双指针找满足条件的边

代码

// 给定一个包含非负整数的数组 nums ，返回其中可以组成三角形三条边的三元组个数
int triangleNumber(vector<int>& nums) {
    std::sort(nums.begin(), nums.end()); // 先排序数组
    
    int n = nums.size(), count = 0;
    
    // 外层for循环 控制最大数
    for(int i = n - 1; i >= 1; --i)
    {
        int left = 0, right = i - 1;
        
        while(left < right)
        { 
            if(nums[left] + nums[right] <= nums[i])   left++;
            else { // 如果 left + right > 最大数，则区间内的所有left与right组合均满足三角形
                count += right - left;
                right--;
            }
        }
    }
    
    return count;
}

---

LCR179.查找总价格为目标值的两个商品

思路

• 解法一：暴力枚举
  • 通过两层for循环，判断是否满足条件
  • 时间开销大，O(n^2)

for(int i = 0; i < n; ++i)
	for(int j = i + 1; j < n - 1; ++j)
		check(nums[i] + nums[j] == target);

• 解法二：利用单调性使用双指针法
  1. 题目要求找到数组中任意两个和为target的数：

代码

vector<int> twoSum(vector<int>& price, int target) {
    int n = price.size();
    int left = 0, right = n - 1;
    while(left < right)
    {
        int sum = price[left] + price[right]; // 记录两数和
        if(sum < target)
            left++;
        else if (sum > target)
            right--;
        else 
            return {price[left], price[right]};
    }
    return {};
}

---

15.三数之和

思路

1. 题目要求找到数组中三个不同的位置，满足nums[i] + nums[j] + nums[k] == 0，并找到所有满足条件的三元组：

• 解法一：排序+暴力枚举+使用set去重

• 解法二：排序+双指针法
  

代码

vector<vector<int>> threeSum(vector<int>& nums) {
    // 排序数组 便于后面去重等
    std::sort(nums.begin(), nums.end());
    
    int n = nums.size();
    vector<vector<int>> ret;

    // for循环固定第一个数，则固定的数后的序列进行“找和为target的两个数”
    // 如果 i = -5, 则target = 5
    for(int i = 0; i < n - 2; ++i)
    {
        // 如果固定的数重复，跳过重复的数
        if(i > 0 && nums[i] == nums[i-1])    continue;

        int left = i + 1, right = n - 1;
        while(left < right)
        {
            int sum = nums[i] + nums[left] + nums[right];
            if(sum < 0)
            {
                left++;
            }   
            else if(sum > 0)
            {
                right--;
            }
            else // 找到满足的数，插入到ret中，并更新left和right
            {
                ret.push_back({nums[i], nums[left], nums[right]});
                
                // 判断left和right的下一位是否重复，如果重复则跳过重复的数
                while(left < right && nums[left] == nums[left+1]) {
                    left++;
                }
                while(left < right && nums[right] == nums[right-1]) {
                    right--;
                }

                left++, right--;
            }
        }
    }
    return ret;
}

---

思路

代码