复习拉普拉斯变换

以下截图均来自于西北工业大学卢京潮教授自动控制原理的ppt

复数有关的概念

解析的意思就是：?复函数在这个自变量处是光滑的。

拉氏变换

?

注：正弦函数的拉氏变换推导过程使用了欧拉公式

拉氏变换的几个重要定理：

?例2是求单位脉冲的拉氏变换，单位脉冲用符号δ(t)表示，是在t = 0时刻取值为无穷大，其他时刻取值为零的信号。满足：。

单位阶跃函数是单位脉冲函数的积分，对单位阶跃求一次导就是单位脉冲。单位阶跃积一次分就是单位斜坡。

?实位移定理举的例子是方波信号，时延了a。

?初值定理主要解决当时域函数（原像）不知道，但是知道复域函数（像函数），求其初始值时（也就是t趋近于0），可以转换成求s趋近于无穷时sF(s)的极限。

?和初值定理相似。也是原像不知道，但是像函数知道，可以使用终值定理求原像当t趋近于无穷时原像的值。一般在分析系统是用于计算系统的稳态误差。

?应用：使用拉氏变换方法解微分方程：

?拉式变换小结

（1）常见的拉氏变换

?（2）拉式变换的重要定理

拉式反变换

?第一种方法直接使用后反演公式进行计算；第二种方法使用查表法，具体操作就是先试用试凑法或者留数法将其进行部分分式分解成常见的函数的拉氏变化，一般使用的留数法。

?

?使用上 面的第二种方法解微分方程，其中可以看到这个系统的单位脉冲响应实际上就是所有的特征根对应的模态的线性组合。

?关于模态：

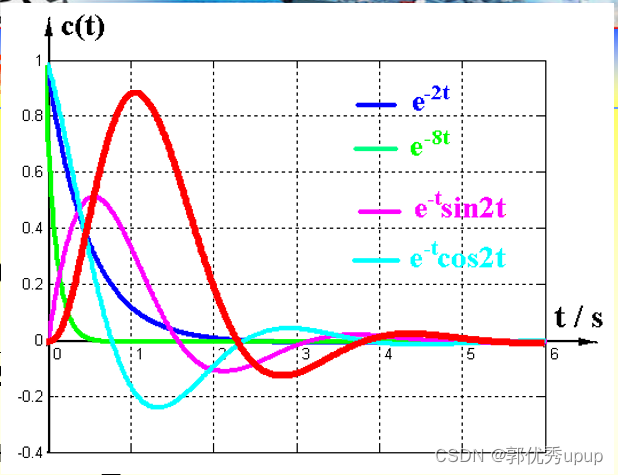
举例说明：下面是一个四阶的系统，输入是一个单位脉冲，现在看其所对应的单位脉冲响应。

其中k(t)就是单位脉冲输入后系统的响应，大红色线就是所有特征根对应的模态的线性组合，可以将其理解为这个模态是构成这个系统单位脉冲响应最简单的形式。