Python实战：计算向量夹角及相关系数

一、实战概述

• 今天我们将通过计算两个向量之间的夹角来探讨它们的相关性。在数据分析、机器学习以及物理学等领域中，向量间的关系是一种强有力的工具，用于表达数据间的依赖和趋势。接下来，我将展示如何使用Python中的NumPy库来实现这一目标。

二、计算向量夹角

（一）思路分析

• 代码主要功能是计算两个向量之间的夹角，并通过这个角度来推断它们的相关性。使用Python的NumPy库来进行高效计算。

1. 导入numpy库

   • import numpy as np，NumPy提供了大量的数学函数和矩阵运算功能，可以方便地处理数组、计算模长、点积等操作。

2. 定义函数included_angle(a, b)

   • 计算输入向量a和b的模长（长度）：分别通过对每个元素平方求和再开方得到。
   • 计算两向量的点积（内积）：np.dot(a, b)，这代表了两个向量在方向上的相似程度。
   • 根据点积公式cos(θ) = A·B / (|A|*|B|) 计算余弦值，其中θ为两向量的夹角。
   • 使用arccos函数(np.arccos)将余弦值转换为弧度表示的夹角。
   • 将弧度转换为角度（以度为单位）：乘以180并除以π。
   • 最后返回计算得到的角度值。

3. 实例化多个向量对

   • 分别定义了三个示例向量对x和y，并调用included_angle函数计算它们之间的夹角。
   • 每次计算后打印出原向量及对应的夹角值。

• 通过这种方法，我们可以直观地了解到两个向量间的方向关系以及它们的相关性。例如，当夹角接近0时，说明两个向量正相关且相关性强；而夹角接近180度时，则意味着两者负相关且相关性强。夹角为90度则表明两个向量不相关。

（二）代码实现

1、创建程序，计算向量夹角

• 创建Python程序 - 计算向量夹角.py
  
• 这段代码定义了一个名为included_angle的函数，用于计算两个输入向量（a, b）之间的夹角。首先，利用NumPy库计算两个向量的模长，然后通过点积公式求出两向量间余弦值，再利用反余弦函数得到弧度表示的夹角，并转换为角度。接下来，作者实例化了三个不同的二维数组对（x, y），分别计算它们的夹角并打印输出。夹角大小反映了向量间的相关性：锐角表明正相关，钝角负相关，直角则不相关。

2、运行程序，查看结果

• 可以看到夹角的三种情况
  
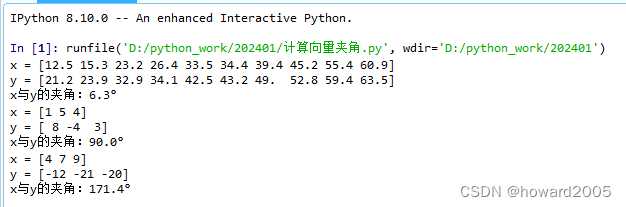
• 向量x和y代表了两个具有多个数值特征的数据序列。通过计算它们的夹角为多少度，我们可以推断它们的相关性。如果夹角是一个锐角（小于90度），则说明这两个向量正相关，且角度越小，正相关性越强；反之，若夹角为钝角（大于90度且小于180度），则说明二者负相关，角度越大，负相关性越明显。当夹角为直角时，说明两个向量不相关；而夹角为零度，则意味着两个向量完全正相关；夹角达到180度时，表明它们完全负相关。

三、计算向量相关系数

（一）相关系数概念

• 计算向量相关系数是统计学中用于衡量两个随机变量之间线性关联程度的方法。在多变量分析和数据分析领域，尤其是在处理数值型数据时，相关系数是一个非常重要的工具。对于向量形式的数据，可以将每个变量看作一个维度上的分量，通过计算这些向量之间的相关系数来评估它们在统计意义上的相互依赖关系。

• 样本相关系数：对于两个一维向量（或者说变量）X和Y，其样本相关系数（记作r）是通过计算协方差与各自标准差的乘积之比得到的。

  $r_{xy}=\frac{\sum _{i=1}^n(x_i?\bar{x})(y_i?\bar{y})}{\sqrt{\sum _{i=1}^n(x_i?\bar{x}{)}^2}\sqrt{\sum _{i=1}^n(y_i?\bar{y}{)}^2}}$

  • $r_{xy}$ 表示变量X和Y之间的皮尔逊样本相关系数。
  • $x_i$ 和 $y_i$ 分别代表第i个观测点上变量X和Y的值。
  • $\bar{x}$ 和 $\bar{y}$ 分别是变量X和Y的样本均值。
  • n 是样本容量（即观测值的数量）。

• r的取值范围在-1到1之间，正值表示正相关，负值表示负相关，0表示无线性相关。

（二）相关系数作用

• 相关系数帮助识别变量间的线性依存模式，如上升、下降趋势或没有趋势。
• 作为预测模型中的重要指标，有助于确定哪些变量对目标变量有显著影响。
• 在投资组合优化、风险评估等领域，通过计算资产收益率间的相关系数可以衡量资产之间的风险分散效应。
• 在科学研究中，相关系数可以帮助研究者推断不同测量变量间是否存在因果联系（但请注意，相关性并不等同于因果性）。

（三）案例演示相关系数的计算

1、创建程序，计算相关系数

• 创建Python程序 - 计算向量相关系数.py
  

"""
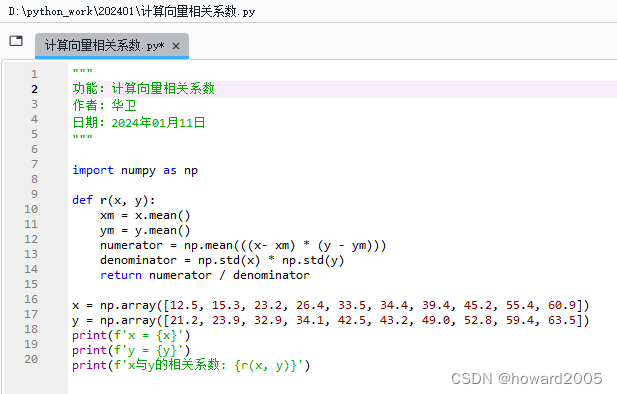
功能：计算向量相关系数
作者：华卫
日期：2024年01月11日
"""

import numpy as np

def r(x, y):
    xm = x.mean()
    ym = y.mean()
    numerator = np.mean(((x- xm) * (y - ym)))
    denominator = np.std(x) * np.std(y)
    return numerator / denominator

x = np.array([12.5, 15.3, 23.2, 26.4, 33.5, 34.4, 39.4, 45.2, 55.4, 60.9])
y = np.array([21.2, 23.9, 32.9, 34.1, 42.5, 43.2, 49.0, 52.8, 59.4, 63.5])
print(f'x = {x}')
print(f'y = {y}')
print(f'x与y的相关系数: {r(x, y)}')

• 该代码段定义了一个名为r的函数，用于计算两个一维NumPy数组（向量）x和y之间的皮尔逊样本相关系数。首先，通过调用NumPy库中的mean()方法分别计算两向量的平均值xm和ym。接着，计算协方差的估计值作为分子部分，即求取(x-xm) * (y-ym)的元素积后取均值。然后，通过求解两向量的标准差并相乘得到分母部分。最后，将分子除以分母得到相关系数，并返回结果。

• 在实际应用中，示例创建了两个包含10个浮点数元素的一维数组x和y，并调用r(x, y)函数计算它们的相关系数，将结果输出到控制台。通过这个相关系数，可以判断x与y之间是否存在线性关系及其强度（正相关、负相关或无相关）。

2、运行程序，查看结果

• x与y正相关：0.9941983762371885
  

三、实战总结

• 本实战通过Python的NumPy库，分别展示了如何计算两个向量之间的夹角以及相关系数，以揭示它们之间的线性关联程度。首先，我们通过计算夹角直观展现了数据序列间方向关系，其中锐角、钝角和直角分别对应正相关、负相关及不相关。接着，我们定义了函数included_angle用于求解向量夹角，并实例化多个向量对进行演示。然后，介绍了计算样本相关系数的方法，并在代码中实现了皮尔逊相关系数的计算函数r(x, y)，该函数利用协方差与各自标准差的比值来衡量变量间的线性依赖。最后，通过对具体一维数组（向量）x和y应用此函数，得出它们具有高度正相关的结论。这些统计工具在数据分析、机器学习等众多领域中都有着广泛的应用价值。