1月11日代码随想录513找树左下角的值

513.找树左下角的值

给定一个二叉树的?根节点?root，请找出该二叉树的?最底层?最左边?节点的值。

假设二叉树中至少有一个节点。

示例 1:

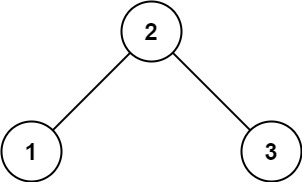
输入: root = [2,1,3]
输出: 1

示例 2:

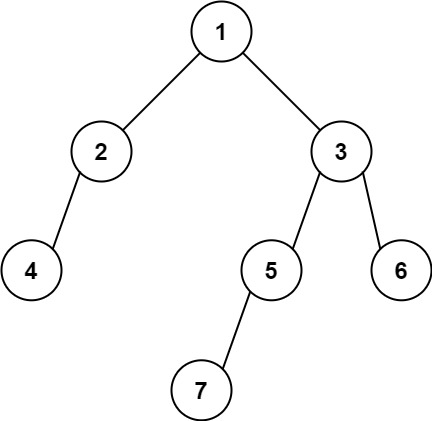
输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7

提示:

• 二叉树的节点个数的范围是?[1,104]
• -231?<= Node.val <= 231?- 1?

思路

广度优先搜索

找到最后一层的最左边的节点，这个题目很直观地能够想到层序遍历一层一层往下走然后到最后一层找最左侧的节点，但是有一个问题，如果按照之前写的层序遍历，判断遍历结束的条件是队列为空，但是在所有节点遍历完之前无法判断当前层是否为最后一层，所以每次都要把当前层第一个存入队列的数记录，这可以是一种方法，但是我们可以换一种思路，就是将遍历的顺序做一个小调换，每次先找右节点再找左节点，这样的话遍历的最后一个节点必定是最后一层最左侧的节点，我们只需要在层序遍历中加一个队列判空就可以存储答案的值，非常巧妙。

class Solution {
    public int findBottomLeftValue(TreeNode root) {
        if(root==null){
            return 0;
        }
        Queue<TreeNode> queue=new LinkedList<TreeNode>();
        queue.offer(root);
        int ans=0;
        while(!queue.isEmpty()){
            int length=queue.size();
            for(int i=0;i<length;i++){
                TreeNode node=queue.poll();
                if(node.right!=null){
                    queue.offer(node.right);
                }
                if (node.left != null) {
                    queue.offer(node.left);
                }
                if(queue.isEmpty()){
                    ans=node.val;
                }
            }
            
        }
        return ans;
    }
}

深度优先搜索

至于深搜法在这道题目里我认为不是很直观，使用height记录当前遍历到的节点的高度，curVal记录在curHeight深度最左侧节点的值，在搜索时先搜索左子树在搜索右子树，因为先遍历左子树再遍历右子树，所以必定是当前层最左侧的值先被遍历到。

class Solution {
    int curVal=0;
    int curHeight=0;

    public int findBottomLeftValue(TreeNode root) {
        int curHeight=0;
        dfs(root,curHeight);
        return curVal;
    }
    public void dfs(TreeNode root,int height){
        if(root==null){
            return;
        }
        height++;
        dfs(root.left,height);
        dfs(root.right,height);
        if(height>curHeight){
            curHeight=height;
            curVal=root.val;
        }
    }
}

总结

这道题目还是适合广搜法的思想一点，深搜的递归思想需要一定的熟练度。