二分查找与搜索树的高频问题(算法村第九关白银挑战)

基于二分查找的拓展问题

山峰数组的封顶索引

852. 山脉数组的峰顶索引 - 力扣（LeetCode）

给你由整数组成的山脉数组 arr ，返回满足 arr[0] < arr[1] < ... arr[i - 1] < arr[i] > arr[i + 1] > ... > arr[arr.length - 1] 的下标 i 。

你必须设计并实现时间复杂度为 O(log(n)) 的解决方案。

提示：

• 3 <= arr.length <= 105
• 0 <= arr[i] <= 106
• 题目数据保证 arr 是一个山脉数组

二分查找

public int peakIndexInMountainArray(int[] arr)
{
    int low = 1;    //mid - 1 >= 0
    int high = arr.length - 2;  // mid + 1 <= arr.length - 1

    while (low <= high)
    {
        int mid = low + (high - low >> 1);

        //找到山峰
        if(arr[mid] > arr[mid - 1] && arr[mid] > arr[mid + 1])
            return mid;
        //山峰左侧(递增)
        else if(arr[mid] > arr[mid - 1] && arr[mid] < arr[mid + 1])
            low = mid + 1;
        //山峰右侧（递减）
        else
            high = mid - 1;
    }

    return -1;
}

旋转排序数组的最小值

无重复元素

153. 寻找旋转排序数组中的最小值 - 力扣（LeetCode）

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

• 若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
• 若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

二分查找

nums [pivot] >= nums [high] 时，移动 low

public int findMin(int[] nums)
    {
        int left = 0;
        int right = nums.length - 1;

        while (left < right)  // left == right 时找到最低点(最小值)
        {
            int mid = left + (right - left >> 1);

            if(nums[mid] < nums[right])
                right = mid; //让 right 去触碰最低点(因为无法确定mid是不是最低点下标，故不能跳过它。如果是比较数值，那可以直接跳过，即 right = mid + 1)
            else
                left = mid + 1;  // left 迫近最低点，与 right 汇合
        }

        return nums[left];   //left == right == mid
    }

有重复元素

154. 寻找旋转排序数组中的最小值 II - 力扣（LeetCode）

二分查找

重复元素要一个个排除

public int findMin(int[] nums)
    {
        int left = 0;
        int right = nums.length - 1;

        while (left < right)  // left == right 时找到最低点(最小值)
        {
            int mid = left + (right - left >> 1);

            if(nums[mid] < nums[right])
                right = mid; //让 right 去触碰最低点
            else if(nums[mid] > nums[right])
                left = mid + 1;  // left 迫近最低点，与 right 汇合
            else
                right--; //处理重复元素要一步一步来
        }

        return nums[left];   //left == right == mid
    }

缺失的数字

剑指 offer ：一个长度为 n - 1 的递增排序数组中的所有数字都是唯一的，每个数字的范围都是 [0,n-1] 。在范围 0～n-1 内的 n 个数字中有且只有一个数字不在该数组中，请找出这个数字。

LCR 173. 点名 - 力扣（LeetCode）

某班级 n 位同学的学号为 0 ~ n-1。点名结果记录于升序数组 records。假定仅有一位同学缺席，请返回他的学号。

示例 1:

输入: records = [0,1,2,3,5]
输出: 4

示例 2:

输入: records = [0, 1, 2, 3, 4, 5, 6, 8]
输出: 7

提示：

1 <= records.length <= 10000

二分查找

public static int missingNumber(int[] nums)
{
    int left = 0;
    int right = nums.length - 1;

    while (left <= right)
    {
        int mid = left + (right - left >> 1);

        if (nums[mid] == mid)
            left = mid + 1; //让 left 去触碰缺失的元素，碰到后就不动了，交给 right 结束循环
        else
            right = mid - 1;
    }

    return left;
}

public static void main(String[] args)
{
    // n = 3 个数字, 数组长度(元素个数)为 n - 1 = 2, 元素范围 [0,2]
    int[] nums = {0, 1};
    System.out.println(missingNumber(nums)); // 输出 2

    // n = 7 个数字, 数组长度(元素个数)为 n - 1 = 6, 元素范围 [0,6]
    int[] nums2 = {0, 1, 2, 3, 5, 6};
    System.out.println(missingNumber(nums2)); // 输出 4
}

x 的平方根

LCR 072. x 的平方根 - 力扣（LeetCode）

给定一个非负整数 x ，计算并返回 x 的平方根，即实现 int sqrt(int x) 函数。

正数的平方根有两个，只输出其中的正数平方根。

如果平方根不是整数，输出只保留整数的部分，小数部分将被舍去。

示例 1:

输入: x = 4
输出: 2

示例 2:

输入: x = 8
输出: 2
解释: 8 的平方根是 2.82842...，由于小数部分将被舍去，所以返回 2

提示:

• 0 <= x <= 231 - 1

二分查找实现

public int mySqrt(int x)
{
    int left = 1;
    int right = x;
    int ans = 0;

    while (left <= right)
    {
        int mid = left + (right - left >> 1);

        if(x / mid >= mid)  //x >= mid2
        {
            ans = mid;  //向下取整逼近答案
            left = mid + 1;
        }
        else
            right = mid - 1;
    }

    return ans;
}

更多题目

34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣（LeetCode）

875. 爱吃香蕉的珂珂 - 力扣（LeetCode）

29. 两数相除 - 力扣（LeetCode）

中序遍历与搜索树

简单来说，如果一棵二叉树是搜索树，则中序遍历序列是一个递增序列。

比较规范的定义是：

• 若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值;
• 若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值;

它的左、右子树也分别为二叉排序树。

下面两棵树的中序序列分别是{3,6,9,10,14,16,19}，{3,6,9,10}，因此都是搜索树。

二叉搜索树中的搜索

700. 二叉搜索树中的搜索 - 力扣（LeetCode）

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。

示例 1:

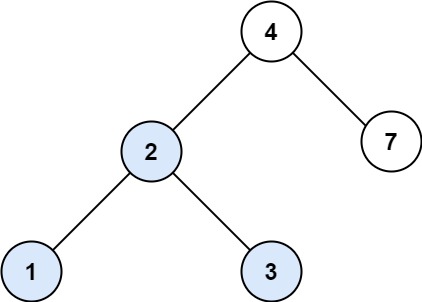
输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]

示例 2:

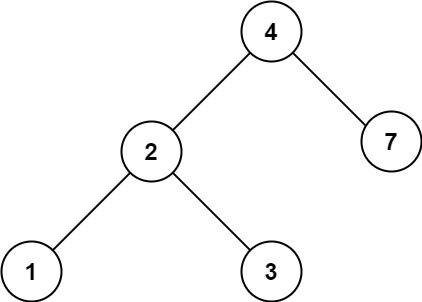
输入：root = [4,2,7,1,3], val = 5
输出：[]

递归

public TreeNode searchBST(TreeNode root, int val)
{
    if (root == null || root.val == val)
        return root;

    if (val < root.val) //进入左子树搜索
        return searchBST(root.left, val);
    else    //否则进入右子树搜索
        return searchBST(root.right, val);
}

迭代

public TreeNode searchBST(TreeNode root, int val)
{
    while (root != null)
    {
        if (root.val == val)
            break;
        else if (val < root.val)
            root = root.left;
        else
            root = root.right;
    }

    return root;
}

验证二叉搜索树

98. 验证二叉搜索树 - 力扣（LeetCode）

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

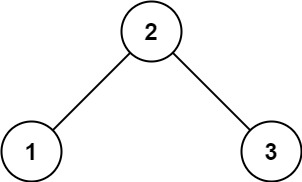
输入：root = [2,1,3]
输出：true

示例 2：

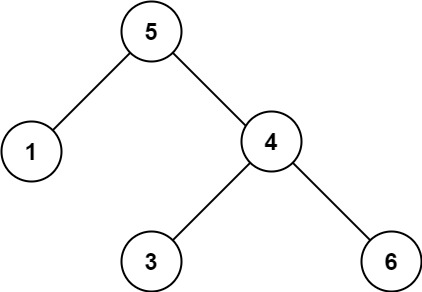
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在[1, 104] 内
• -231 <= Node.val <= 231 - 1

中序遍历+实时检查

二叉搜索树「中序遍历」序列是升序的，所以我们在中序遍历时，实时检查当前节点的值是否大于前一个节点的值即可。

long pre = Long.MIN_VALUE;
public boolean isValidBST(TreeNode root)
{
    if (root == null)
        return true;

    //检查左子树是否为二叉搜索树
    if(!isValidBST(root.left))  //等待左子树的返回结果。如果左子树下某个元素不满足要求，则退出所有递归
        return false;

    //检查当前节点是否大于等于前一个节点
    if (root.val <= pre)
        return false;

    pre = root.val;
    //检查右子树是否为二叉搜索树
    return isValidBST(root.right);  //等待右子树的返回结果
}

中序遍历+是否升序

public boolean isValidBST(TreeNode root)
{
    ArrayList<Integer> res = new ArrayList<>();
    inOrder(root,res);

    for (int i = 1; i < res.size(); i++)
        if (res.get(i - 1) >= res.get(i))
            return false;

    return true;
}

public void inOrder(TreeNode root, ArrayList<Integer> res)
{
    if (root == null)
        return;

    inOrder(root.left, res);
    res.add(root.val);
    inOrder(root.right, res);
}

更多题目

530. 二叉搜索树的最小绝对差 - 力扣（LeetCode）

501. 二叉搜索树中的众数 - 力扣（LeetCode）