快速排序的背后——深入理解时间复杂度

时间复杂度的概念衡量算法性能的重要标准，是算法设计和性能优化中的关键概念，对于编写高效、稳定和可扩展的程序至关重要。但是，初学者对于如何理解和应用时间复杂度则显得较为困难，本文以快速排序为例进一步加深对时间复杂度的理解。

1 回顾

本文侧重于时间复杂度的计算，关于时间复杂度的概念可参考二分查找——算法基础。
首先，我们回顾一下快速排序：

def quicksort(arr):

    if len(arr) < 2:
        return arr
    else:
    	pivot = arr[0]
    	less = [i for i in arr[1:] if i < pivot]
    	greater = [i for i in arr[1:] if i > pivot]
    	return quicksort(less) + [pivot] + quicksort(greater)

在之前的文章中谈过，大O表示法在表示时间复杂度的时候考虑的是最遭的情况，但是由于快速排序的特殊性，需要特别强调平均情况下的时间复杂度。

1 最遭的情况

当我们每次选定的基准值都是无序列表中的最小或最大值的时候，这个时候该算法的时间复杂度与选择排序无差异为$O_{(}{n}^2)$，因为每次进行子集的划分都要对列表内的各个元素操作一次，而像这样的操作要执行n次（调用栈高度为n）。

2 一般情况

但是，当每次选择到的pivot都是集合中大小居中的元素，这个时候操作的子集数为$lo{g}_{2}n$：

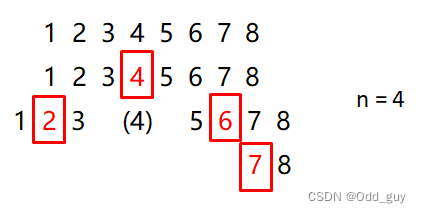
而用户给函数提供的列表多是无序的，所以可以以平均情况下的时间复杂度来表示快速排序的性能，即平均下来，调用栈的高度为$lo{g}_{2}n$，而每次对站内存储的列表元素都要进行对比，所以操作次数为$n$，所以时间复杂度为：
$$O_{nlo{g}_{2}n}\to n?lo{g}_{2}n$$

END