径向基函数插值

一、径向基函数的定义

如果 $||x_1||=||x_2||$，那么 $?(x_1)=?(x_2)$ 的函数 $?$ 就是径向函数，即仅由 $r=||x||$ 控制的函数（径向基函数是一个取值仅仅依赖于离原点距离的实值函数，或者还可以是到任意一点 $c$ 的距离）。

给定一个一元函数 $?：R_{+}\to R$，在定义域 $x\in R^d$ 上，所有形如 $\psi (x)=?(||x?c||)$ 及其线性组合张成的函数空间称为由函数 $?$ 导出的径向基函数空间。

在一定的条件下，只要取 { x j } \{x_j\} {xj?} 两两不同， { ? ( x ? x j ) } \{\phi(x-x_j)\} {?(x?xj?)} 就是线性无关的，从而形成径向基函数空间中某子空间的一组基。当 { x j } \{x_j\} {xj?} 几乎充满 $R$ 时， { x j } \{x_j\} {xj?} 几乎充满 $R$ 时， { ? ( x ? x j ) } \{\phi(x-x_j)\} {?(x?xj?)} 及其线性组合可以逼近几乎任何函数。

各类文献中常用的径向基函数有：

1. Kriging 方法的 Gauss 分布函数：$?(r)=e^{?c^2{r}^2}$
2. Kriging 方法的 Markoff 分布函数：$?(r)=e^{?c|r|}$，及其他概率分布函数；
3. Hardy 的 Multi-Quadric 函数：$?(r)=(c^2+r^2{)}^{\beta }$（其中 $\beta$ 是正的实数）；
4. Hardy 的逆 Multi-Quadric 函数：$?(r)=(c^2+r^2{)}^{?\beta }$（其中 $\beta$ 是正的实数）；
5. Duchon 的薄板样条：$d$ 为偶数时，$?(r)=r^{2k?d}\log r$；$d$ 为奇数时，$?(r)=r^{2k?d}$；

二、径向基函数插值

定义：径向基函数插值是对于给定的多元散乱数据 { x j , f j } j = 1 n , x j ∈ R n , f j ∈ R , j = 1 , ? ? , n \{x_j,f_j\}^n_{j=1},x_j\in R^n,f_j\in R,j=1,\cdots,n {xj?,fj?}j=1n?,xj?∈Rn,fj?∈R,j=1,?,n。选取径向函数 $?:R_{+}\to R$ 来构造函数系 { ? ( ∣ ∣ x ? x j ∣ ∣ ) } j = 1 n \{\phi(||x-x_j||)\}_{j=1}^n {?(∣∣x?xj?∣∣)}j=1n? 并寻找形如 $S(x)={\sum }_{j=1}^n{\lambda }_j?(||x?x_j||)$ 的插值函数 $S(x)$，使其满足条件 $S(x_j)=f_j,j=1,?,n$。

为了方便，我们定义
$$?\begin{array}{l}{f}^T=(f_1,f_2,?,f_n)\\ {?}^T(x)=(?(||x?x_1||,?(||x?x_2||,?,?(||x?x_n||))\\ {\lambda }^T=({\lambda }_1,{\lambda }_2,?,{\lambda }_n)\\ A=(?(||x_j?x_k||){)}_{n\times n}\end{array}$$

上述插值方程对任意两两不同的 $x_j$ 的数据 { x j , f j } \{x_j,f_j\} {xj?,fj?} 有解的充要条件是：对任意两两不同的 $x_j$，对称矩阵 $A$ 都非奇异。

定理：函数 $?:R_{+}\to R$ 是连续的，${\lim }_{r\to \infty }?(r)=0$，那么对于 $n$ 元的径向基函数插值总是存在唯一解的充分条件是：矩阵 $A$ 是正定矩阵。

上面提到的径向基函数中逆 Multi-Quadric 函数和 Gauss 函数在任意维空间上都是正定函数，因此插值是唯一的。

三、用高斯函数进行散乱数据的插值

对于数据量少的情况，径向基函数（尤其是高斯函数）插值的结果较令人满意，而且计算也比较简单。

令径向基函数插值方程为
$$S(x)=\sum _{j=1}^n{\lambda }_j?(||x?x_j||)$$

将已知点 $(x_j,f_j),j=1,?,n$ 代入方程，可得：
$$\left[\begin{array}{cccc}{\lambda }_1& {\lambda }_2& ?& {\lambda }_n\end{array}\right]\left[\begin{array}{cccc}?(||x_1?x_1||)& ?(||x_2?x_1||)& ?& ?(||x_n?x_1||)\\ ?(||x_1?x_2||)& ?(||x_2?x_2||)& ?& ?(||x_n?x_2||)\\ ?& ?& & ?\\ ?(||x_1?x_n||)& ?(||x_2?x_n||)& ?& ?(||x_n?x_n||)\end{array}\right]=\left[\begin{array}{cccc}{f}_1& f_2& ?& f_n\end{array}\right]$$

求解上述方程，可求出 ${\lambda }_1,{\lambda }_2,?,{\lambda }_n$ 的值，从而求出插值曲线方程。插值曲面方程类似，将 $x$ 替换成向量 $X$ 即可。

具体应用到高斯函数，设高斯函数插值方程为
$$S(x)=\sum _{j=1}^n{\lambda }_j{e}^{?\alpha ||x?x_j|{|}^2}\alpha >0$$

其中，$\alpha$ 为形状调整参数，可根据散乱数据点分布特征选取，当数据点对应的函数值变化较大时，$\alpha$ 可取的稍大些；数据点对应的函数值变化较小时，$\alpha$ 可取得稍小些。

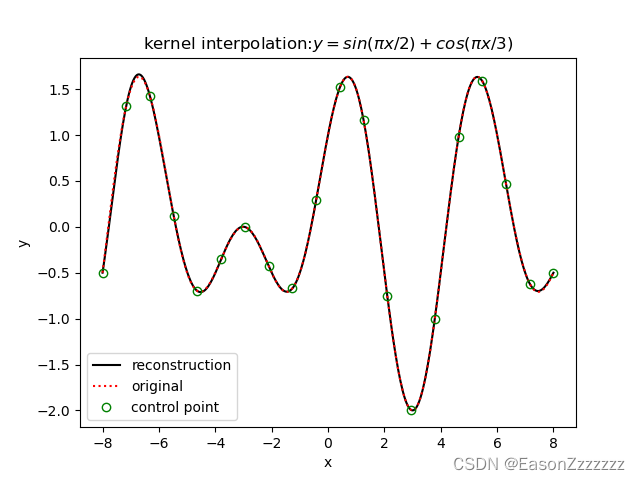
python 代码实现

import numpy as np
import matplotlib.pyplot as plt


def gen_data(x1, x2):
    # 用于生成插值节点和总数据点 x1,x2 分别为插值节点的横坐标构成的行向量，总数据点的横坐标构成的行向量
    y_sample = np.sin(np.pi * x1 / 2) + np.cos(np.pi * x1 / 3)  # 插值节点的函数值
    y_all = np.sin(np.pi * x2 / 2) + np.cos(np.pi * x2 / 3)  # 总数据点的函数值
    return y_sample, y_all


def kernel_interpolation(y_sample, x1, sig):
    # 求解插值函数中高斯基函数的系数
    gaussian_kernel = lambda x, c, h: np.exp(-h*(x - x[c]) ** 2)  # 高斯基函数
    num = len(y_sample)
    w = np.zeros(num)
    int_matrix = np.asmatrix(np.zeros((num, num)))
    for i in range(num):
        int_matrix[i, :] = gaussian_kernel(x1, i, sig)
    w = np.asmatrix(y_sample) * int_matrix.I
    w = w.T
    return w


def kernel_interpolation_rec(w, x1, x2, sig):
    gkernel = lambda x, xc, h: np.exp(-h*(x - xc) ** 2)  # 高斯基函数
    num = len(x2)
    y_rec = np.zeros(num)
    for i in range(num):
        for k in range(len(w)):
            y_rec[i] = y_rec[i] + w[k] * gkernel(x2[i], x1[k], sig)
    return y_rec


if __name__ == '__main__':
    snum = 20  # control point数量
    ratio = 20  # 总数据点数量：snum*ratio
    sig = 0.5  # 核函数宽度
    xs = -8
    xe = 8
    x1 = np.linspace(xs, xe, snum)
    x2 = np.linspace(xs, xe, (snum - 1) * ratio + 1)
    y_sample, y_all = gen_data(x1, x2)
    plt.figure(1)
    w = kernel_interpolation(y_sample, x1, sig)
    y_rec = kernel_interpolation_rec(w, x1, x2, sig)
    plt.plot(x2, y_rec, 'k')
    plt.plot(x2, y_all, 'r:')
    plt.ylabel('y')
    plt.xlabel('x')
    for i in range(len(x1)):
        plt.plot(x1[i], y_sample[i], 'go', markerfacecolor='none')

    plt.legend(labels=['reconstruction', 'original', 'control point'], loc='lower left')
    plt.title('kernel interpolation:$y=sin(\pi x/2)+cos(\pi x/3)$')
    plt.show()

运行结果

Matlab 代码实现