二叉树前,中序推后续_中,后续推前序
发布时间:2023年12月17日
介绍
二叉树是由根、左子树、右子树三部分组成。
二叉树的遍历方式又可以分为前序遍历,中序遍历,后序遍历。
前序遍历:根,左子树,右子树
中序遍历:左子树,根,右子树
后序遍历:左子树,右子树,根
比如定义一棵树:
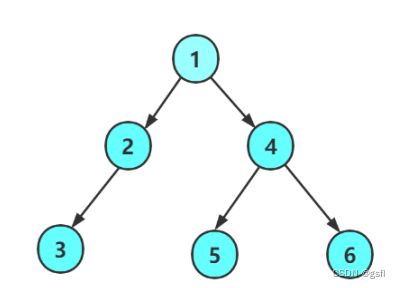
它的前序遍历结果为:1 2 3 4 5 6
中序遍历结果为:3 2 1 5 4 6
后序遍历结果为:3 2 5 6 4 1
现在如果我们没有二叉树的图,只知道它的两种遍历的结果,如何求第三种遍历的结果呢?问题化简一下,我们只需知道完整的数的样子就能直接写出第三种遍历结果,所以我们需要用两种遍历的结果推出树的样子就好了。(两种遍历中必须包含中序遍历,只有前序遍历和后序遍历不能确定一棵树。)
思路
首先观察三种遍历的特点,主要思路就是找根节点的位置。
例子
比如给出一颗二叉树的中序遍历序列为JGDHKBAELIMCF,后序遍历序列为JGKHDBLMIEFCA。
由后续遍历最后一个是根结点,我们可以找到根是A。
再由中序遍历:根的左边是左子树,右边是右子树。所以A的左子树为JGDHKB,A的右子树为ELIMCF。
比较中序遍历的左右子树确定后序遍历中的左右子树
中:JGDHKB A ELIMCF
后:JGKHDB LMIEFC A
再次根据后续遍历找根,可以看出是B和C
然后在中序遍历的左右子树中再次找出根,左子树,右子树。一直重复直到最后只剩一个结点。下面以左子树为例。
2中:JGDHK B 此时没有右子树
2后:JGKHD B
根为D
3中:JG D HK
3后:JG KH D
根为G
4中:J G
4后:J G
所以可以得到树
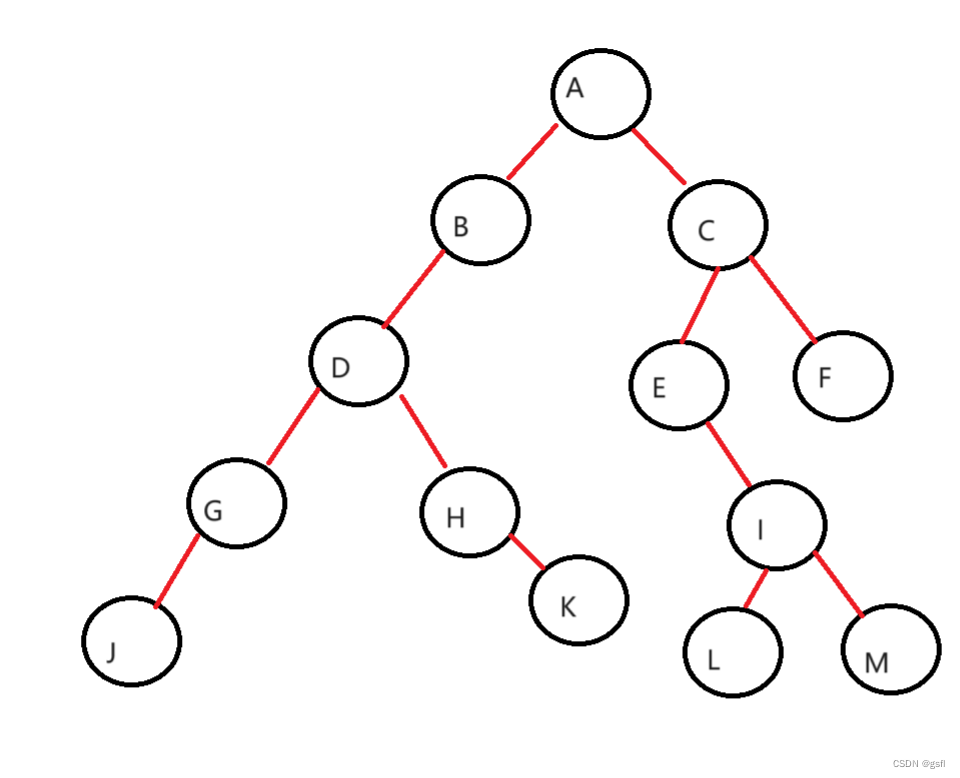
所以它的前序遍历为:ABDGJHKCEILMF
前序+中序推后序与此类似。
文章来源:https://blog.csdn.net/2301_79274600/article/details/135046159
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- JavaScript 获取当前日期时间 年月日 时分秒的方法
- 【CVPR2023】人像卡通化(2D图像->3D卡通)
- vue中最重要的点,双向数据绑定是什么?
- RT-DETR优化改进:IoU系列篇 | Focaler-IoU???????更加聚焦的IoU损失Focaler-IoU |2024年最新发表
- 视频号上怎么开店带货?门槛和注意事项,如下所示
- vue-springboot基于Javaweb的二手儿童绘本网上商城交易系统设计与实现
- 云计算试题
- 1001 A+B Format
- Android 实现获取集合中出现重复数据的值和数量
- ????—设计-建-0造3-者-模式—????