Unity中Shader 齐次坐标
发布时间:2023年12月27日
前言
在之前的文章中,我们进行了正交相机视图空间转化到裁剪空间的推导。
在这篇文章中,我们进行透视相机视图空间转化到裁剪空间的推导的前置准备——齐次坐标是什么。
一、什么是齐次坐标
齐次坐标:就是将一个原本是 n 维的向量 用一个n + 1维向量来表示
二、齐次坐标增加分量 w 的意义
- (x,y,z) -> (x,y,z,w)
1、当 w ≠ \neq = 0时:
可以把式子化简为 (x/w,y/w,z/w,1)
用(1,2,3)为例,以下式子都是等价的:
- (1,2,3)
- (1,2,3,1)
- (2,4,6,2)
- (3,6,9,3)
- (……)
2、当 w = 0时:
(x,y,z,0)表示的是一个无穷远的点
3、用方程组,直观的看一下w的意义
- Ax + By + C = 0(不动的那条线)
- Ax + By + D = 0(下面移动的那条线)
- 若 C ≠ \neq = D,则方程无解
- 若 C = D,则表示的是同一直线
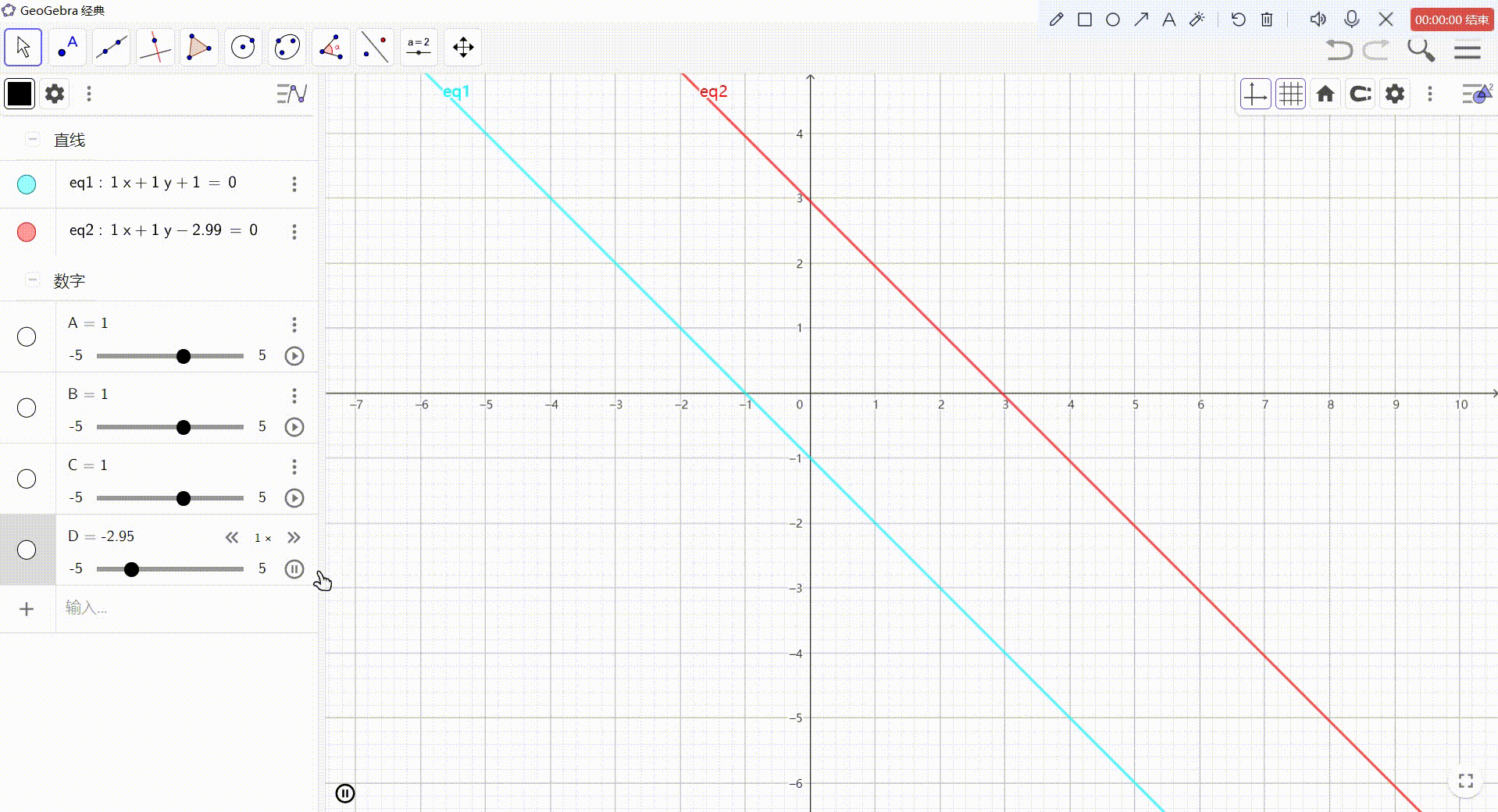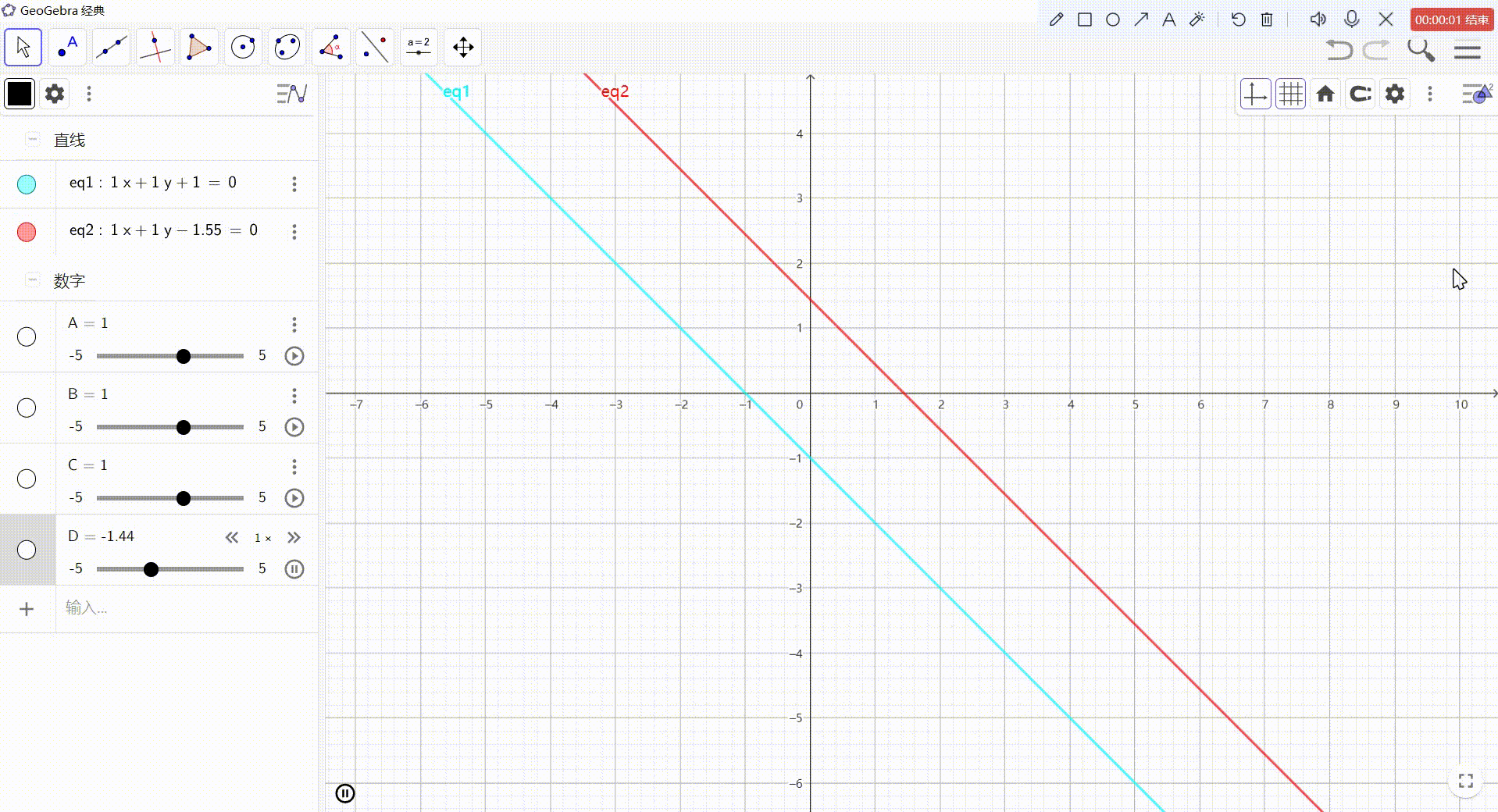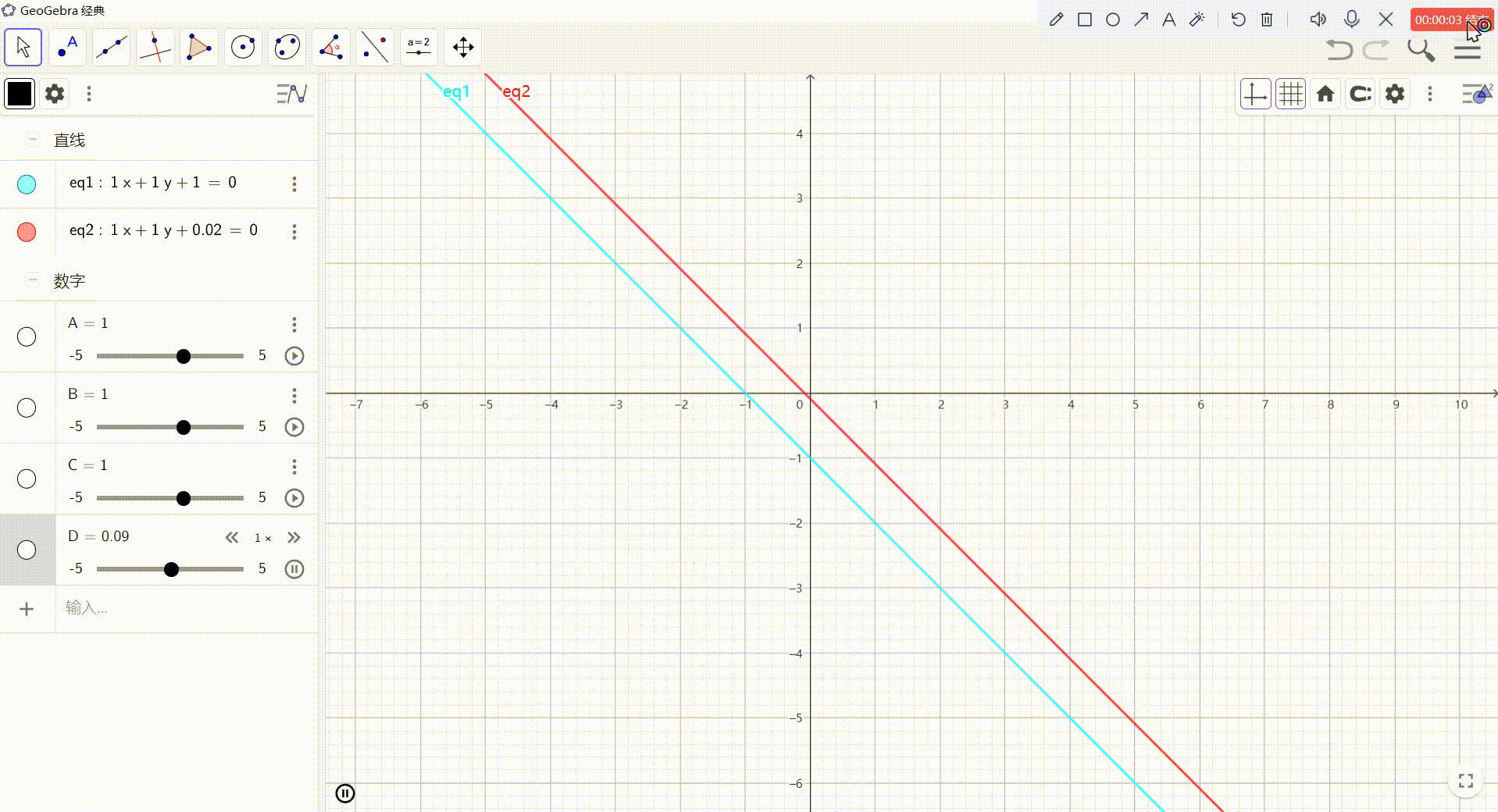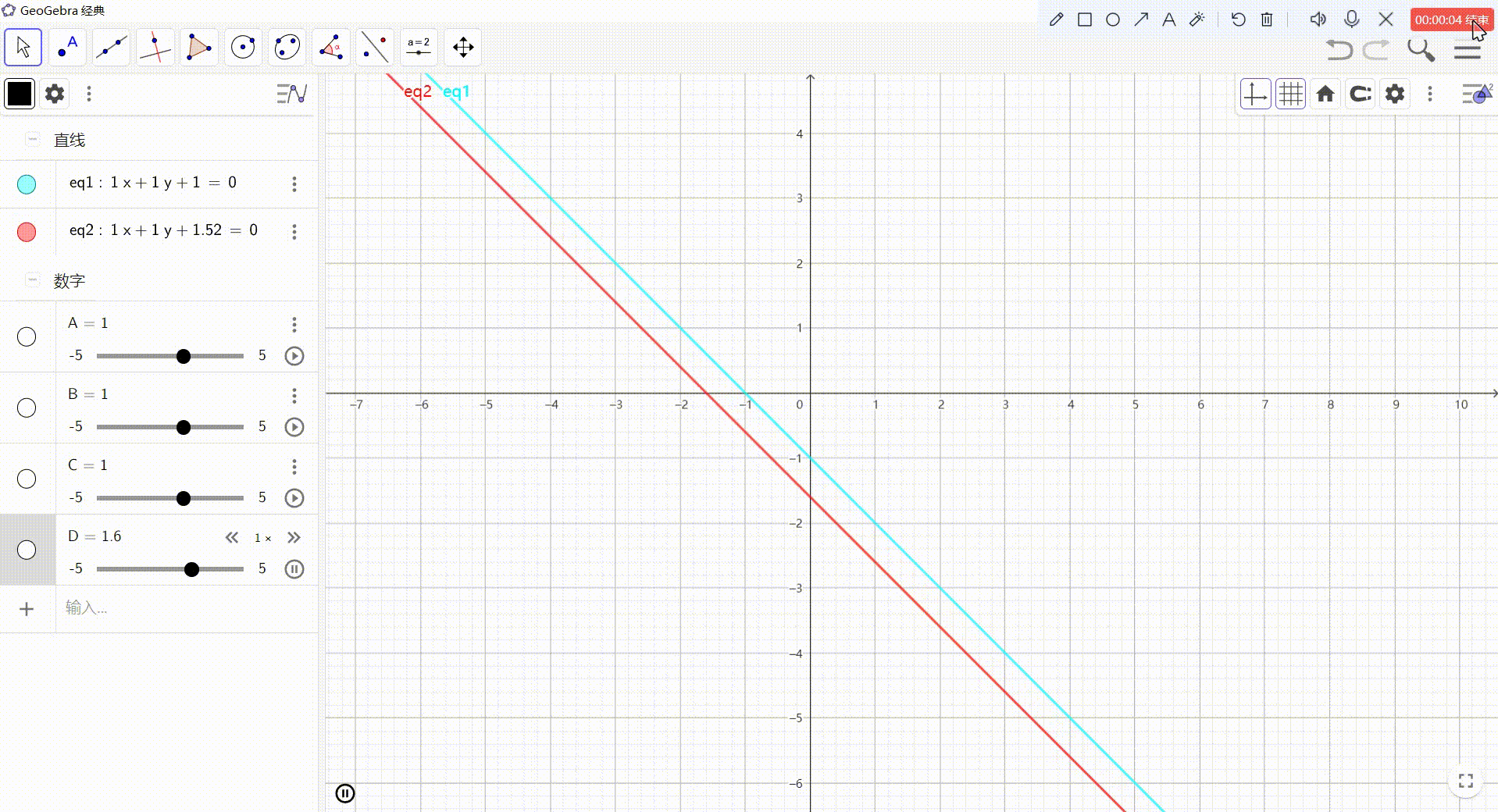
- 此时,我们使用 x w 代替 x \frac{x}{w}代替x wx?代替x, y w 代替 y \frac{y}{w}代替y wy?代替y
- A x w + B y w + C = 0 A\frac{x}{w} + B \frac{y}{w} + C = 0 Awx?+Bwy?+C=0
- A x w + B y w + D = 0 A\frac{x}{w} + B \frac{y}{w} + D = 0 Awx?+Bwy?+D=0
->
- A x + B y + C w = 0 Ax + By + Cw = 0 Ax+By+Cw=0
- A x + B y + D w = 0 Ax + By + Dw = 0 Ax+By+Dw=0
若C
≠
\neq
=D,则有唯一解(x,y,0)
若w = 0,表示的点是无穷远处
文章来源:https://blog.csdn.net/qq_51603875/article/details/135241451
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!