如何理解图卷积网络GCN
基本概念
度矩阵(degree)
度矩阵是对角矩阵,对角上的元素表示每个顶点的度,也就是该顶点相关联的边的数量。
邻接矩阵(Adjacency)
邻接矩阵表示顶点间的关系,矩阵元素为0或1。无向图邻接矩阵是对称矩阵,有向图的邻接矩阵不一定对称。如下图所示
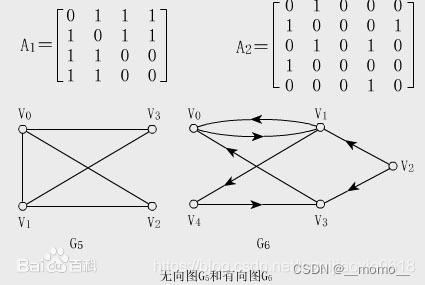
理解GCN
如何理解 Graph Convolutional Network(GCN)?
GCN,图卷积神经网络,实际作用和CNN一样,是一个特征提取器。
假设有一批图数据。图中有 N N N个节点,每个节点都有自己的特征( D D D维),设这些节点特征组成 N ? D N*D N?D维的矩阵 X X X,各个节点之间的关系形成一个 N ? N N*N N?N维的邻接矩阵 A A A。将 X X X和 A A A输入图卷积神经网络。其中 X X X代表节点的特征, A A A代表边的特征。
GCN的传播方式为:
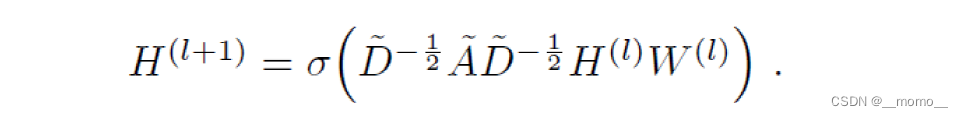
其中,
- A ~ = A + I \tilde{A} = A + I A~=A+I(这一步是为了将node自身的特征进行运算,相当于add self loop)
- D ~ \tilde{D} D~为度矩阵,可以由 A ~ \tilde{A} A~计算得到。 D ~ \tilde{D} D~的作用是将 A ~ \tilde{A} A~归一化,使每行加起来为1。
- σ \sigma σ是激活函数
- H H H是当前层的特征,对于输入层的话,相当于 X X X。
两层GCN
将 D ~ ? 1 / 2 A ~ D ~ ? 1 / 2 \tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2} D~?1/2A~D~?1/2看作一个整体 A ^ \hat{A} A^,则对于一个两层的GCN,激活函数分别采用ReLU和Softmax,整体的正向传播的公式为:
s o f t m a x ( A ^ R e L U ( A ^ X W 0 ) W 1 ) softmax(\hat{A}ReLU(\hat{A}XW^0)W^1) softmax(A^ReLU(A^XW0)W1)
网络层数设置
在GCN网络深度的对比研究中,2-3层就可以达到比较好的效果。
搭建GCN网络
定义GCN层
可以调用 torch_geometric.nn 中的 GCNConv 进行实现。
torch_geometric.nn
class GCNConv(MessagePassing):
def __init__(self, in_channels, out_channels, add_self_loops=True, bias=True):
super(GCNConv, self).__init__()
self.add_self_loops = add_self_loops
self.edge_index = None
self.linear = pyg_nn.dense.linear.Linear(in_channels, out_channels, weight_initializer='glorot')
if bias:
self.bias = nn.Parameter(torch.Tensor(out_channels, 1))
self.bias = pyg_nn.inits.glorot(self.bias)
else:
self.register_parameter('bias', None)
# 1.消息传递
def message(self, x, edge_index):
# 1.对所有节点进行新的空间映射
x = self.linear(x) # [num_nodes, feature_size]
# 2.添加偏置
if self.bias != None:
x += self.bias.flatten()
# 3.返回source、target信息,对应边的起点和终点
row, col = edge_index # [E]
# 4.获得度矩阵
deg = degree(col, x.shape[0], x.dtype) # [num_nodes]
# 5.度矩阵归一化
deg_inv_sqrt = deg.pow(-0.5) # [num_nodes]
# 6.计算sqrt(deg(i)) * sqrt(deg(j))
norm = deg_inv_sqrt[row] * deg_inv_sqrt[col] # [num_nodes]
# 7.返回所有边的映射
x_j = x[row] # [E, feature_size]
# 8.计算归一化后的节点特征
x_j = norm.view(-1, 1) * x_j # [E, feature_size]
return x_j
# 2.消息聚合
def aggregate(self, x_j, edge_index):
# 1.返回source、target信息,对应边的起点和终点
row, col = edge_index # [E]
# 2.聚合邻居特征
aggr_out = scatter(x_j, row, dim=0, reduce='sum') # [num_nodes, feature_size]
return aggr_out
# 3.节点更新
def update(self, aggr_out):
# 对于GCN没有这个阶段,所以直接返回
return aggr_out
def forward(self, x, edge_index):
# 2.添加自环信息,考虑自身信息
if self.add_self_loops:
edge_index, _ = add_self_loops(edge_index, num_nodes=x.shape[0]) # [2, E]
return self.propagate(edge_index, x=x)
self.propagate 会依次调用message, aggregate, update,完成消息的传递、聚合、更新。
定义GCN网络
class GCN(nn.Module):
def __init__(self, num_node_features, num_classes):
super(GCN, self).__init__()
self.conv1 = GCNConv(num_node_features, 16)
self.conv2 = GCNConv(16, num_classes)
def forward(self, data):
x, edge_index = data.x, data.edge_index
x = self.conv1(x, edge_index)
x = F.relu(x)
x = F.dropout(x, training=self.training)
x = self.conv2(x, edge_index)
return F.log_softmax(x, dim=1)
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 软件验收测试计划、验收测试报告案例模板参考
- SQL和NoSQL数据库的全面比较
- 一篇文章掌握系统架构的演变和常见微服务框架
- vue3 vuedraggable draggable element must have an item slot
- InsCode实践分享
- django《区块链技术与应用》课程案例信息资源系统(程序+开题报告)
- 拥有Acrobat DC、Visio软件,办公技能让你独步全世界!
- int char[] String 转换
- <软考高项备考>《论文专题 - 54 进度管理(5) 》
- 维也纳整流电路笔记