【遥感数字图像处理（朱文泉）】第三章 空间域处理方法

3 1 空间域处理方法概述

?一、空间域与变换域
?二、常见数字图像空间域处理方法

一、空间域与变换域

? - 空间域处理方法是根据图像像元数据的空间表示f(x, y)进行处理；
? - 变换域处理方法是对图像像元数据的空间表示f(x, y)先进行某种变换，然后针对变换数据进行处理，最后再把处理的结果反变换到空间域。注意：变换域处理一定有正变换和反变换，如果没有反变换处理的话，在变换域里处理的图像没法在空间域里进行显示。

?? 注意：不是所有的变换域图像都没有空间结构。比如，经过主成分变换的变换域图像有空间结构信息。

二、常见数字图像空间域处理方法

? - 空间域处理方法分为：数值运算、集合运算、逻辑运算、数学形态运算。

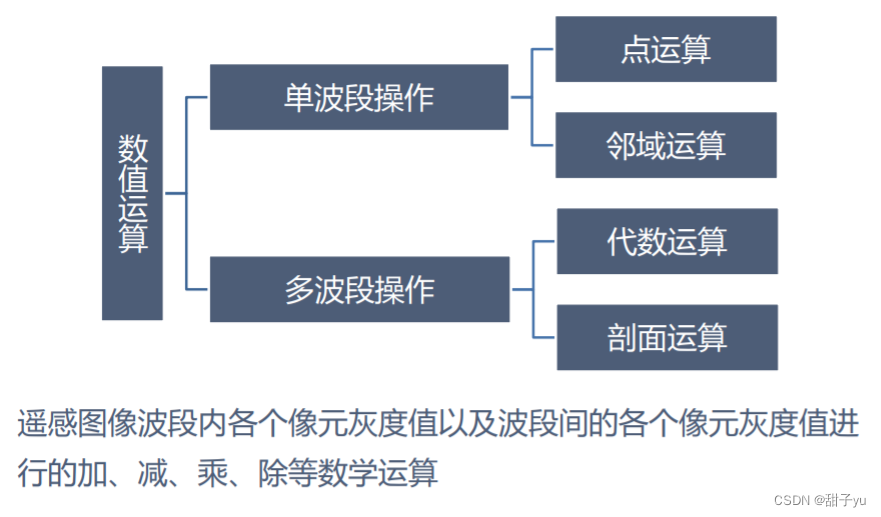
3 2 数值运算：单波段点运算

?一、线性点运算
?二、分段线性点运算
?三、非线性点运算

一、线性点运算

? - 点运算是对单幅图像像元进行的逐像元数值运算，它将输入图像映射为输出图像，输出图像每个像元的灰度值仅由对应的输入像元点的灰度值决定，它不会改变图像内像元之间的空间关系。若输入图像为f(x，y)，输出图像为g(x，y)，则点运算可表示为：

g(x,y) = T[f(x,y)] ?T为灰度变换函数，可为任意函数，根据灰度变换函数的不同，点运算又可分为线性点运算、分段线性点运算和非线性点运算。

二、分段线性点运算

??注意这里的图像，横坐标是输入，纵坐标是输出。

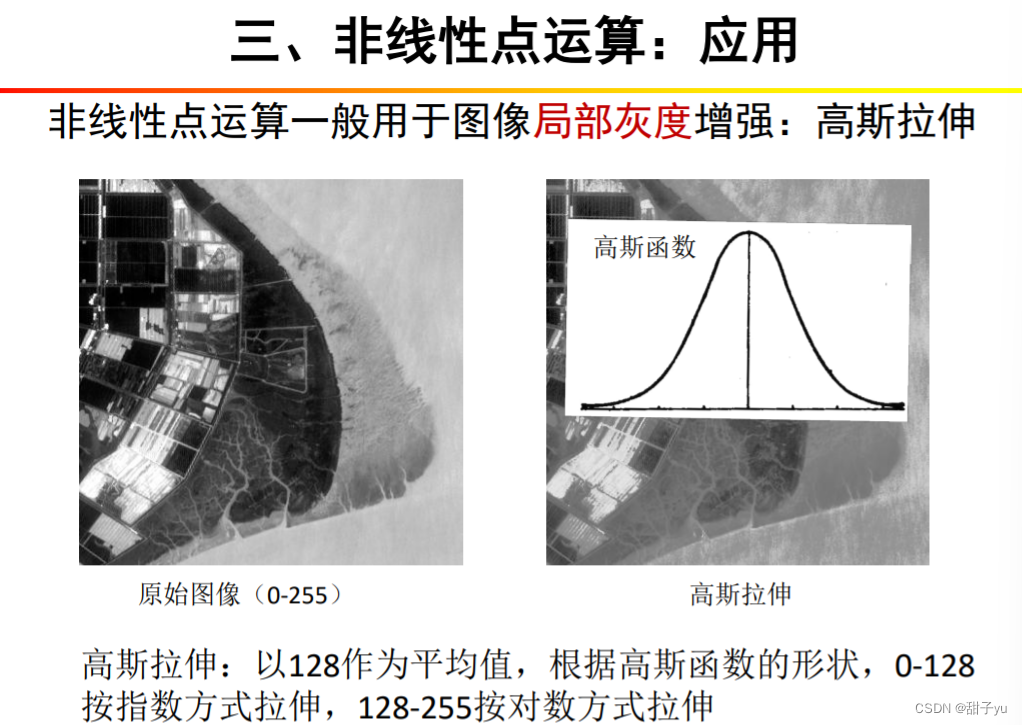
三、非线性点运算

? - 非线性变换的函数有很多，常用的有指数变换和对数变换。
??注意这里的图像，横坐标是输入，纵坐标是输出。例如：图(a)前半部分，输入部分宽，输出部分窄，说明压缩了暗的部分。

3 3 数值运算：单波段邻域运算

? 一、邻域窗口
? 二、卷积运算
? 三、邻域统计

? 邻域运算是指输出图像中每个像元的灰度值是由对应的输入像元及其邻域内的像元灰度值共同决定的图像运算。

一、邻域窗口

? 邻域运算的具体做法是先定义一个邻域窗口，该邻域窗口通常只用来定义参与运算的邻域范围，如果邻域窗口对应为一个M×N（M、N通常为奇数）的数字矩阵，则称之为模板窗口。将原图像像元在邻域窗口中进行运算，将运算后的值赋给输出图像中对应于邻域窗口中心的像元。
? 邻域窗口根据其在运算过程中的不同平移方式，又可以分为滑动窗口和跳跃窗口。

?要注意，滑动窗口进行计算时，周边的一圈像元是没办法处理的。这个办法怎么解决呢？
?解决的方式一般有两种。如果我们处理的结果（这幅图像和原图像）灰度值代表同样的意义，比如去噪声处理（去噪声之前和去噪声之后代表同样的意义），这时我们一般先复制出一幅结果图像（把结果图像和原图像相同地复制一份），只是改变中间的值，边上的值还是保留原图像的值；第二种处理方式，就是直接把这个处理结果复制给原图像。

二、卷积运算

? 图像卷积运算就是将模板在输入图像中逐像元移动，每到一个位置就把模板的值与其对应的像元值进行乘积运算并求和，从而得到输出图像对应于模板中心位置的像元灰度值。

三、邻域统计

? 1、算法

? 常见的邻域统计包括求和、均值、标准差、最大值、最小值、众数、少数、多样性、密度、秩统计等。

? - 多样性统计
? ? 逐步统计输入图像在邻域窗口中所包含的像元类型个数（一个唯一灰度值对应于一种类型的像元），并将此值赋给输出图像对应于邻域窗口中心的像元。

? - 密度统计
? ? 逐步统计某一灰度值（通常为输入图像在邻域窗口中心的像元值）在输入图像邻域窗口所覆盖区域内出现的次数，并将此值赋给输出图像对应于邻域窗口中心的像元。 ? - 秩统计
??逐步统计输入图像在邻域窗口所覆盖区域内灰度值小于中心像元（输入图像对应于模板中心的像元）灰度值的像元个数（即中心像元灰度值在邻域窗口中由小到大的序号），并将此值赋给输出图像对应于邻域窗口中心的像元。

3 4 数值运算：多波段运算

? 一、代数运算
? 二、剖面运算

一、代数运算

? 图像的代数运算是指对多幅（两幅或两幅以上）输入图像进行的像元对像元的数学运算。常见的代数运算有：
? 加法运算可以把同一场景的多幅图像加起来求平均，从而可有效降低图像中的随机噪声。
? 减法运算可用于突出图像中的研究对象，通过去除背景效果，能够去除部分系统影响，从而突出观测物体本身。
? 乘法运算可以用来遮盖图像中的某些部分（图像掩膜）。
? 除法运算常用于产生比率图像，这对于多光谱图像的分析十分有用。
? 代数运算：归一化差值植被指数（NDVI）计算

二、剖面运算

? 剖面运算是指对多波段图像像元所构成的剖面进行的波段间的数值运算。

? - 剖面运算步骤：
? ? 1、提取剖面
? ? 2、开展单波段相关运算
? - 注意：多波段数据构成的剖面有“真”和“假”之分，主要是Z轴不同。真：Z轴是空间数据；假：一幅时间序列的遥感图像就是类三维空间数据（它的第三维（Z轴）实际上是对应于时间维，而不是通常意义上的空间维）。

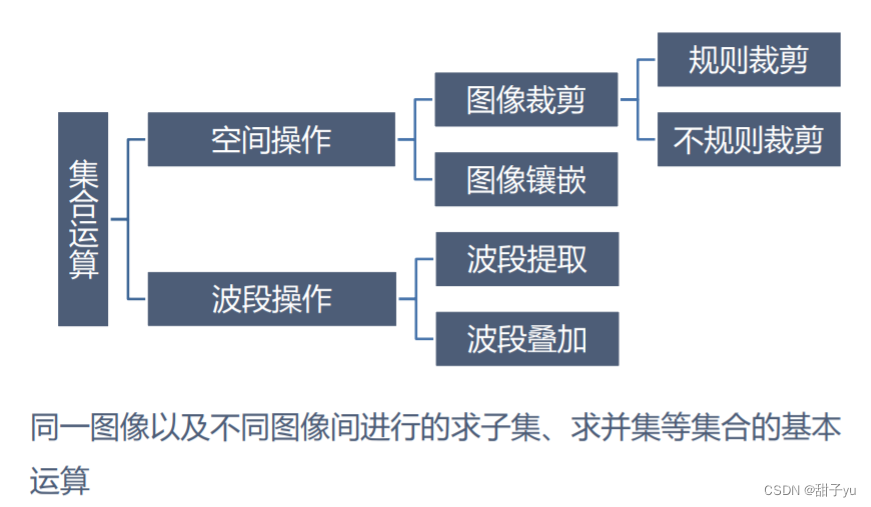
3 5 集合运算：空间操作

? 一、图像裁剪
? 二、图像镶嵌

一、图像裁剪

? 图像裁剪的目的是为了保留图像中需要感兴趣的部分，将感兴趣区之外的部分去除。

? - 注意事项：如果图像裁剪不是最终的处理步骤，此时需尽可能使裁剪后的图像比实际的研究区 略微大一些，以免给图像的后续处理带来问题。 ?1、注意事项——投影变换 （很明显可以看出，裁剪后进行投影变换的图像是存在缺失值的，是不正确的。尤其还要考虑到滑动窗口周边像元缺失） ?2、注意事项——计算坡度 （DEM计算坡度，DEM就是数字高程模型数据，它每一个像元代表的是一个地表的高度、高程。其计算高度：把两个像元的高度差除以像元的分辨率，就是两个像元中间的一个距离，即一个坡度。下图展示DEM两种计算方案，白色圈是人为画上去的，是研究区。而最后一个图像很明显的白色圈不是人为加上去的，而是通过裁剪后边缘值和研究区内的边缘值计算得到的，是不正确的，说明完全按照研究区裁剪是有问题的）

二、图像镶嵌

?图像镶嵌是在统一的空间坐标系下，把多景相邻遥感图像拼接成一幅大范围、无缝的图像。

? - 注意事项：图像镶嵌的过程可以形象地比喻成衣服的缝补过程，若要使衣服上的补丁看不出异常，缝补过程需注意以下3个要点：
??① 尽量选择与衣服一致的布料（如相同的颜色和质地）。 对于图像镶嵌来说，待镶嵌的图像在重叠区应该具有 相似的色调、纹理等特征。 ??②缝合线尽量选择在布料不同颜色或图案的交界处，以减少违和感。对于图像镶嵌来说， 拼接线尽量选择在差异明显的自然地物交界处，如河流（河两边的自然地物一般变化较大）、路、山脊（山的南北景观差异明显）。 ??③ 缝补后需用熨斗熨平补丁。对于图像镶嵌来说，如果拼接线两边的色调差异较大，则需考虑对拼接线两边附近的图像作 匀色处理。 ? - 图像镶嵌步骤：
??（1）选择图像，设计镶嵌方案。
??（2）图像几何配准。
??（3）相邻图像颜色匹配。
??（4）图像镶嵌。需考虑重叠区的图像选择问题，为此需要先在重叠区内绘制一条连接两边图像的拼接线，使得根据这条拼接线拼接起来的新图像浑然一体，不露拼接的痕迹。

3 6 集合运算：波段操作

?一、波段提取
?二、波段叠加

一、波段提取

?波段提取是指从一个多波段的图像文件中提取某一个特定波段作为一个独立的文件。如选择某些光谱波段进行遥感分类。

二、波段叠加

?波段叠加是指将同一地理范围不同波段的文件合并为一个多波段文件。波段叠加对各图像文件有以下要求：
??（1）同一场景的图像；
??（2）图像具有相同的空间坐标系；
??（3）图像文件的尺寸大小相同，即具有相同的行列数。
?如将多时相的遥感数据叠加在一起开展时序分析。

3 7 逻辑运算

?一、求反运算
?二、与运算
?三、或运算
?四、异或运算
?五、逻辑运算综合应用示例

重点：逻辑运算综合应用

?逻辑运算又称布尔运算，逻辑常量只有两个，即0和1，用来表示两个对立的逻辑状态“假”和“真”。逻辑变量与普通代数变量一样，可以用字母、符号、数字及其组合来表示，当进行逻辑运算时逻辑变量需先通过某种规则转换为逻辑常量。

一、求反运算

二、与运算

三、或运算

四、异或运算

五、逻辑运算综合应用示例

?逻辑运算的作用：以农作物旱灾监测为例，如果有植被净初级生产力（NPP）监测结果和土壤水分监测结果。

3 8 数学形态学运算

?一、二值形态学运算
??腐蚀、膨胀、开运算、闭运算
?二、灰度形态学运算
??腐蚀、膨胀、开运算、闭运算

难点：二值形态学运算与灰度形态学运算的区别
重点：数学形态学运算在图像处理中的应用

?数学形态学是以形态为基础对图像进行分析的数学工具，在图像去噪声、图像增强、图像分割等处理中应用较广。
?数学形态学操作可以分为二值形态学和灰度形态学，灰度形态学是由二值形态学扩展而来。基于数学形态学的图像处理有两个基本运算，即腐蚀和膨胀，而以腐蚀和膨胀为基础又形成了开运算和闭运算。

一、二值形态学运算

?1、腐蚀
??腐蚀是一种消除边界点，使边界向内部收缩的过程，可以用来消除小且无意义的目标物。用结构元素B腐蚀二值图像A可以定义为：

式中，(B)xy表示将结构元素B的原点平移到图像像元(x, y)位置。如果B在图像像元(x, y)处完全包含在A中（也就是B中为1的元素位置上对应的A图像值全部为1），则将输出图像对应的像元(x, y)赋值为1，否则赋值为0。 ?2、膨胀
??膨胀是将与目标区域接触的背景点 合并到该目标物中，使目标边界向外部扩张的处理。膨胀可用来填补目标区域中某些空洞以及消除包含在目标区域中的小颗粒噪声。用结构元素B对图像A膨胀可以定义为：

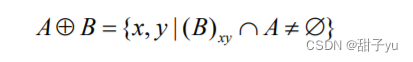
式中，(B)xy表示将结构元素B的原点平移到图像像元(x, y)位置。如果B在图像像元(x, y)处与A的交集不为空（也就是B中为1的元素位置上对应的A图像值至少有一个为1），则将输出图像对应的像元(x, y)赋值为1，否则赋值为0。

二、灰度形态学运算

?我们结构元素里的值都是正值，所以用原始图像减结构元素的值，再求最小值，那么它的值就降低了，所以输出之后，它的灰度值就下降了，即可以把一个高值变低，可以应用于去噪声处理中（去峰值噪声）。 ?我们结构元素里的值都是正值，这是一个相加操作，再求最大值，所以结果图像值变大。这里可以应用于去低谷噪声。