2023-12-11 LeetCode每日一题(最小体力消耗路径)
发布时间:2023年12月31日
2023-12-11每日一题
一、题目编号
1631. 最小体力消耗路径
二、题目链接
三、题目描述
你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ,其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ,且你希望去最右下角的格子 (rows-1, columns-1) (注意下标从 0 开始编号)。你每次可以往 上,下,左,右 四个方向之一移动,你想要找到耗费 体力 最小的一条路径。
一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。
请你返回从左上角走到右下角的最小 体力消耗值 。
示例 1:

示例 2:
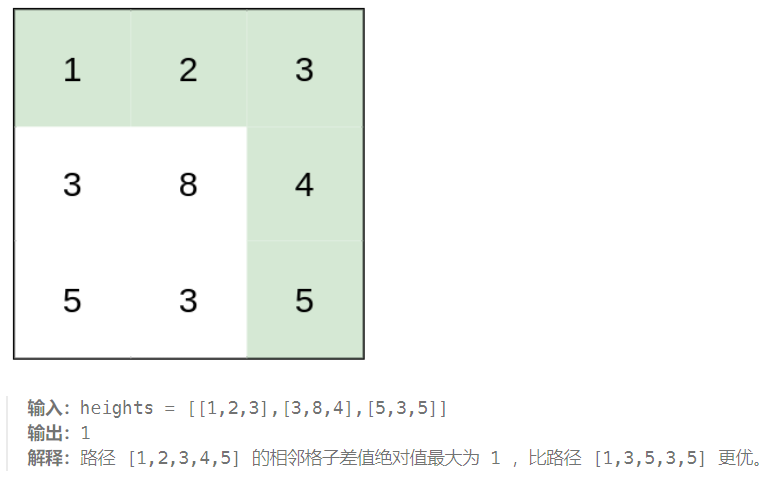
示例 3:

提示:
- rows == heights.length
- columns == heights[i].length
- 1 <= rows, columns <= 100
- 1 <= heights[i][j] <= 106
四、解题代码
int dir[4][2] = {
{-1, 0},
{1, 0},
{0, -1},
{0, 1}
};
const int maxn = 101;
bool bfs(int height, vector<vector<int>>& heights, int m, int n){
int hash[maxn * maxn + 100 + 6];
memset(hash, 0, sizeof(hash));
queue<int> path;
path.push(0 * 100 + 0);
hash[0 * 100 + 0] = 1;
while(!path.empty()){
int tmp = path.front();
path.pop();
int x = tmp / maxn;
int y = tmp % maxn;
if(x == m - 1 && y == n - 1){
return true;
}
for(int i = 0; i < 4; ++i){
int tx = x + dir[i][0];
int ty = y + dir[i][1];
if(tx >= m || ty >= n || tx < 0 || ty < 0){
continue;
}
if(hash[tx * maxn + ty] == 0 && abs(heights[tx][ty] - heights[x][y]) <= height){
hash[tx * maxn + ty]=1;
path.push(tx * maxn + ty);
}
}
}
return false;
}
class Solution {
public:
int minimumEffortPath(vector<vector<int>>& heights) {
int left = 0, right = 999999;
int ans = 0;
int m = heights.size();
int n = heights[0].size();
while(left <= right){
int mid = (left+right) >> 1;
if(bfs(mid, heights, m, n) == true){
ans = mid;
right = mid-1;
}
else{
left = mid + 1;
}
}
return left;
}
};
五、解题思路
(1) 利用图的四方向遍历。
(2) 二分答案来求解。
(3) 广度优先搜索来判断答案可不可行。
文章来源:https://blog.csdn.net/qq_56086076/article/details/135318879
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 修复“找不到服务器IP地址”错误
- 复试 || 就业day04(2024.01.05)项目一
- 虹科分享 | 用Redis为LangChain定制AI代理——OpenGPTs
- FPGA LCD1602驱动代码 (已验证)
- JVM-2-对象
- 1130 - Host 182.244.45,94‘ is not allowed to connect to this MySQL server
- 共享类数据——class data share功能
- 【MySQL】逻辑架构
- CSS3-——过渡
- 2024年游泳耳机十大品牌排行榜,游泳耳机哪个牌子好?