复试 || 就业day04(2024.01.05)项目一

发布时间：2024年01月05日

文章目录

前言

💫你好，我是辰chen，本文旨在准备考研复试或就业
💫本文内容来自某机构网课，是我为复试准备的第一个项目
💫欢迎大家的关注，我的博客主要关注于考研408以及AIoT的内容
🌟 预置知识详见我的AIoT板块，需掌握 基本Python语法, Numpy, Pandas, Matplotlib

以下的几个专栏是本人比较满意的专栏(大部分专栏仍在持续更新)，欢迎大家的关注：

💥ACM-ICPC算法汇总【基础篇】
💥ACM-ICPC算法汇总【提高篇】
💥AIoT(人工智能+物联网)
💥考研
💥CSP认证考试历年题解

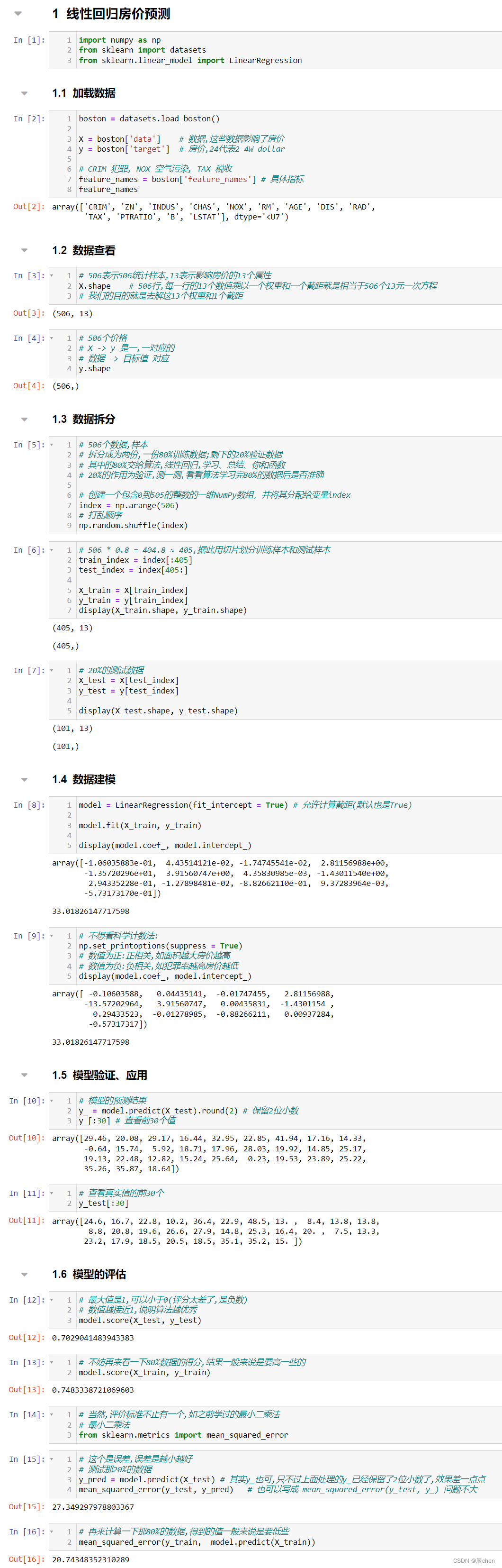
线性回归房价预测

import numpy as np
from sklearn import datasets
from sklearn.linear_model import LinearRegression

加载数据

boston = datasets.load_boston()

X = boston['data']    # 数据,这些数据影响了房价
y = boston['target']  # 房价,24代表2 4W dollar 

# CRIM 犯罪, NOX 空气污染, TAX 税收
feature_names = boston['feature_names'] # 具体指标
feature_names

在这里插入图片描述

数据查看

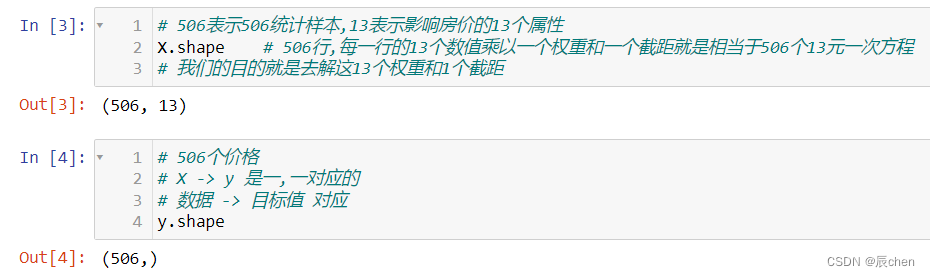
# 506表示506统计样本,13表示影响房价的13个属性 
X.shape    # 506行,每一行的13个数值乘以一个权重和一个截距就是相当于506个13元一次方程
# 我们的目的就是去解这13个权重和1个截距

# 506个价格
# X -> y 是一,一对应的
# 数据 -> 目标值 对应
y.shape

在这里插入图片描述

数据拆分

# 506个数据,样本
# 拆分成为两份,一份80%训练数据;剩下的20%验证数据
# 其中的80%交给算法,线性回归,学习、总结、你和函数
# 20%的作用为验证,测一测,看看算法学习完80%的数据后是否准确

# 创建一个包含0到505的整数的一维NumPy数组，并将其分配给变量index
index = np.arange(506)
# 打乱顺序
np.random.shuffle(index)

# 506 * 0.8 = 404.8 ≈ 405,据此用切片划分训练样本和测试样本
train_index = index[:405]
test_index = index[405:]

X_train = X[train_index]
y_train = y[train_index]
display(X_train.shape, y_train.shape)

# 20%的测试数据
X_test = X[test_index]
y_test = y[test_index]

display(X_test.shape, y_test.shape)

在这里插入图片描述

数据建模

model = LinearRegression(fit_intercept = True) # 允许计算截距(默认也是True)

model.fit(X_train, y_train)

display(model.coef_, model.intercept_)

# 不想看科学计数法:
np.set_printoptions(suppress = True)
# 数值为正:正相关,如面积越大房价越高
# 数值为负:负相关,如犯罪率越高房价越低
display(model.coef_, model.intercept_)

在这里插入图片描述

模型的验证、应用

# 模型的预测结果
y_ = model.predict(X_test).round(2) # 保留2位小数
y_[:30] # 查看前30个值

# 查看真实值的前30个
y_test[:30]

在这里插入图片描述

模型的评估

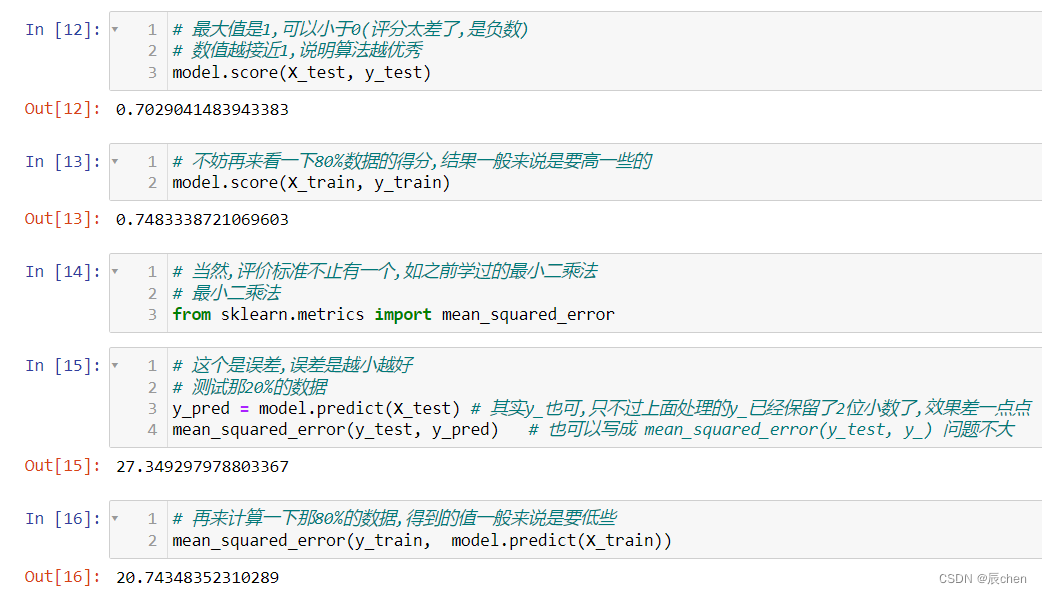
# 最大值是1,可以小于0(评分太差了,是负数)
# 数值越接近1,说明算法越优秀
model.score(X_test, y_test)

# 不妨再来看一下80%数据的得分,结果一般来说是要高一些的
model.score(X_train, y_train)

# 当然,评价标准不止有一个,如之前学过的最小二乘法
# 最小二乘法
from sklearn.metrics import mean_squared_error

# 这个是误差,误差是越小越好
# 测试那20%的数据
y_pred = model.predict(X_test) # 其实y_也可,只不过上面处理的y_已经保留了2位小数了,效果差一点点
mean_squared_error(y_test, y_pred)   # 也可以写成 mean_squared_error(y_test, y_) 问题不大

# 再来计算一下那80%的数据,得到的值一般来说是要低些
mean_squared_error(y_train,  model.predict(X_train))

在这里插入图片描述

总结

完整代码：

import numpy as np
from sklearn import datasets
from sklearn.linear_model import LinearRegression 

boston = datasets.load_boston()

X = boston['data']    # 数据,这些数据影响了房价
y = boston['target']  # 房价,24代表2 4W dollar 
# X.shape : (506, 13), y.shape : (506, )

# CRIM 犯罪, NOX 空气污染, TAX 税收
feature_names = boston['feature_names'] # 具体指标

# 创建一个包含0到505的整数的一维NumPy数组，并将其分配给变量index
index = np.arange(506)
# 打乱顺序
np.random.shuffle(index)

# 506个数据,样本
# 拆分成为两份,一份80%训练数据;剩下的20%验证数据
# 其中的80%交给算法,线性回归,学习、总结、你和函数
# 20%的作用为验证,测一测,看看算法学习完80%的数据后是否准确
# 506 * 0.8 = 404.8 ≈ 405,据此用切片划分训练样本和测试样本
train_index = index[:405]
X_train = X[train_index]
y_train = y[train_index]

# 20%的测试数据
test_index = index[405:]
X_test = X[test_index]
y_test = y[test_index]

# 不想看科学计数法:
np.set_printoptions(suppress = True)
model = LinearRegression(fit_intercept = True) # 允许计算截距(默认也是True)
# 数值为正:正相关,如面积越大房价越高
# 数值为负:负相关,如犯罪率越高房价越低
model.fit(X_train, y_train)

# 模型的预测结果
y_ = model.predict(X_test).round(2) # 保留2位小数
# 最大值是1,可以小于0(评分太差了,是负数)
# 数值越接近1,说明算法越优秀
model.score(X_test, y_test)

# 不妨再来看一下80%数据的得分,结果一般来说是要高一些的
model.score(X_train, y_train)

# 当然,评价标准不止有一个,如之前学过的最小二乘法
# 最小二乘法
from sklearn.metrics import mean_squared_error
# 这个是误差,误差是越小越好
# 测试那20%的数据
y_pred = model.predict(X_test) # 其实y_也可,只不过上面处理的y_已经保留了2位小数了,效果差一点点
mean_squared_error(y_test, y_pred)   # 也可以写成 mean_squared_error(y_test, y_) 问题不大
# 再来计算一下那80%的数据,得到的值一般来说是要低些
mean_squared_error(y_train,  model.predict(X_train))

在这里插入图片描述

文章来源:https://blog.csdn.net/qq_52156445/article/details/135418743
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章