Speech | 人工智能中关于语音务必需要了解的基础知识(信号处理)及代码

语音是指人们讲话时发出的话语，是一种人们进行信息交流的声音，是由一连串的音组成语言的声音，我们可以理解为语音(speech)=声音(acoustic)+语言(language)。

目录

0.声音的基本属性

0.1.音高(pitch)

0.2.音量(Volume)

0.3.音色(Timbre)

0.4.能量(Energy)

1.傅里叶变换(FT)

1.1.快速傅里叶变换 （FFT）

1.2.短时傅里叶变换 （STFT）

1.2.短时傅里叶逆变换 （iSTFT）

2.频谱图

3.梅尔量表

4.梅尔倒谱系数（Mel-frequency Cepstral Coefficients, MFCC）

梅尔频谱图(mel-spectrogram)

总结

---

关于语音研究主要可分为两个方面：语言学和语音学。

0.声音的基本属性

【8】由于语音是发声器官发出的一种声波，因而具有一定的音色、音调、音强和音长等基本特征。

• 音调：表示声音的高低，由于声波的频率决定。
• 音强：表示声音的强弱，由声波的振动幅度决定。
• 音色：即音质，是一种声音区别于另一种声音的基本特征，其与声带的振动频率、发音器官的送气方式，声道的形状尺寸等因素密切相关，是一种对各种频率、强度的声波的综合反应，
• 音长：发音时间的长短

0.1.音高(pitch)

在语音中，耳朵感知到的音调的相对高低，这取决于声带每秒产生的振动次数。音高是音调和语调（qq.v.）的主要声学相关性。

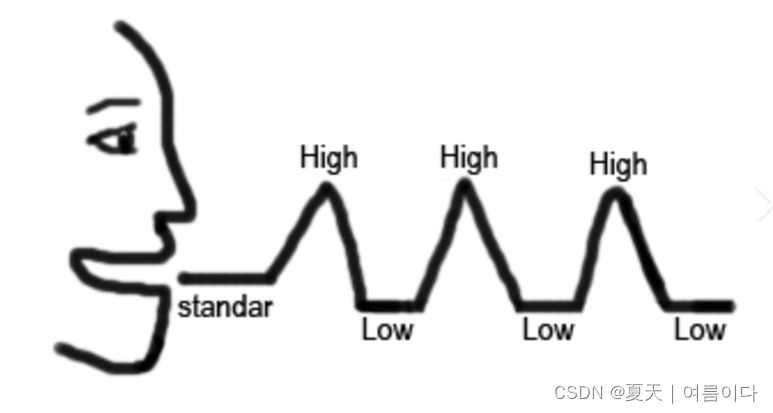
0.2.音量(Volume)

音量通常可以用振幅（Amplitude）或分贝（Decibels，dB）来表示。振幅表示声音的振动强度，而分贝则是用对数单位来表达声音的相对强度。

在语音合成中，音量的调整可以通过控制振幅或分贝来实现，以确保生成的语音在听觉上具有合适的音量水平。

0.3.音色(Timbre)

音色是声音的质地或音质，通常由声音的谐波结构和频谱特征来描述。

在语音合成中，可以使用谐波合成或者声码器参数（如倒谱系数）来表示音色。调整音色可以使得合成语音更加自然，并匹配特定的语音风格或说话者特征。

0.4.能量(Energy)

能量通常用于描述声音的强度或活力。在语音信号中，能量可以通过短时能量、功率谱等来表示。

能量的调整可以影响语音的清晰度和强度。在语音合成中，适当地调整能量可以使合成语音听起来更加生动和富有表现力。

1.傅里叶变换(FT)

频信号由几个单频声波组成。当随时间对信号进行采样时，我们只捕获由此产生的振幅。傅里叶变换是一个数学公式，它允许我们将信号分解为它的各个频率和频率的幅度。换句话说，它将信号从时域转换为频域。结果称为频谱。

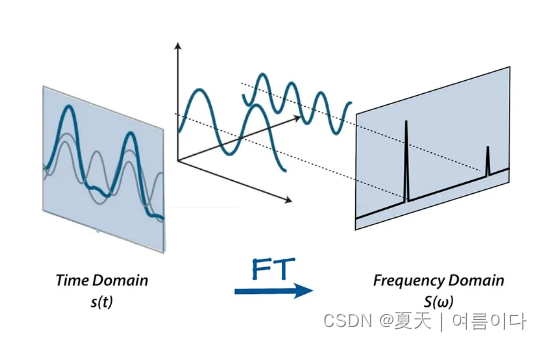
?因为每个信号都可以分解为一组正弦波和余弦波，这些正弦波加起来就是原始信号。这是一个非凡的定理，称为傅立叶定理。

1.1.快速傅里叶变换 （FFT）

FFT是一种可以有效计算傅里叶变换的算法，用于将信号从时域转换到频域。它是对传统傅里叶变换算法的一种改进，能够大大提高计算速度。

傅里叶变换的目的： 将一个信号从时域表示转换为频域表示，即将信号表示为不同频率分量的叠加。

FFT算法基于分治法和迭代的思想，通过将信号划分为较小的子问题，然后合并这些子问题的结果来实现傅里叶变换。主要步骤如下：

• 划分： 将输入信号划分为偶数索引和奇数索引的两部分，分别进行傅里叶变换。
• 递归： 对划分后的子问题进行递归应用FFT算法。
• 合并： 合并子问题的结果，得到整体的傅里叶变换。

从技术上讲，FFT是实现“离散傅里叶变换”（DFT）的优化算法。在一段时间内对信号进行采样，并划分为频率分量。这些分量是单个正弦频率，每个分量都有自己的幅度和相位。下图演示了此转换。在测量的时间段内，信号包含三个不同的主频率。

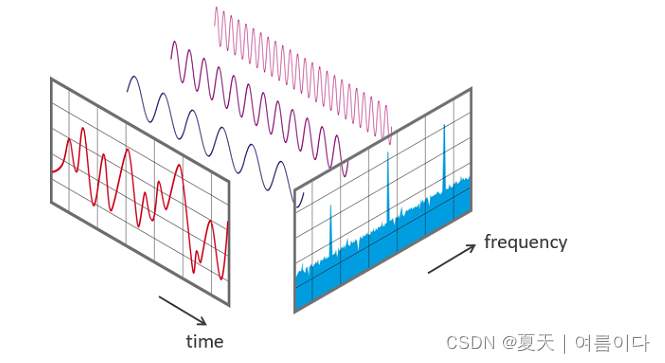
?在第一步中，扫描一部分信号并将其存储在内存中以供进一步处理。在这种情况下，这两个参数是相关的：

• 测量系统的采样率或采样频率fs（例如48 kHz）。这是在 1 秒内获得的平均样本数（每秒样本数）。
• 选择的样本数量;块长度 BL。这始终是 FFT 中以 2 为基数的整数倍（例如，2^10 = 1024 个样本）

从两个基本参数 fs 和 BL 可以确定测量的其他参数:Bandwidth fn?(= Nyquist frequency)

该值表示可由FFT确定的理论最大频率,也就是max wav value。

1.2.短时傅里叶变换 （STFT）

STFT 是信号在时间上分段，并在每个时间段内进行傅里叶变换的过程。通过这种方式，可以得到信号在时间和频率上的局部表示。

步骤：

1. 将信号分帧，形成许多短时窗口。
2. 对每个窗口应用傅里叶变换，得到每个窗口的频谱。
3. 沿着时间轴滑动窗口，重复步骤2，直到覆盖整个信号。

# pip install torch-stft
import torch
from torch_stft import STFT
import numpy as np
import librosa 
import matplotlib.pyplot as plt

audio = librosa.load(librosa.util.example_audio_file(), duration=10.0, offset=30)[0]
device = 'cpu'
filter_length = 1024
hop_length = 256
win_length = 1024 # doesn't need to be specified. if not specified, it's the same as filter_length
window = 'hann'

audio = torch.FloatTensor(audio)
audio = audio.unsqueeze(0)
audio = audio.to(device)

stft = STFT(
    filter_length=filter_length, 
    hop_length=hop_length, 
    win_length=win_length,
    window=window
).to(device)

magnitude, phase = stft.transform(audio)
output = stft.inverse(magnitude, phase)
output = output.cpu().data.numpy()[..., :]
audio = audio.cpu().data.numpy()[..., :]
print(np.mean((output - audio) ** 2)) # on order of 1e-16

1.2.短时傅里叶逆变换 （iSTFT）

iSTFT(inverse?short-time fourier transforms)是将经过STFT处理的频域表示恢复为时域表示的逆过程。

步骤：

1. 对每个频谱进行逆傅里叶变换，得到每个窗口的时域表示。
2. 将所有时域表示进行叠加，得到完整的时域信号。

如果STFT的结果表示为X(t, f)，其中t是时间，f是频率，那么iSTFT可以表示为：

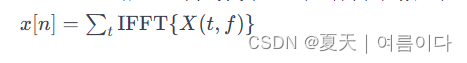
iSTFT的目标是重建原始信号，但在实践中，由于STFT通常使用了窗函数和重叠，因此可能存在信号重建时的失真。

为了减小这种失真，通常需要在STFT中使用适当的窗函数，并调整窗口的长度和重叠参数。

更多细节可查看【4】

2.频谱图

频谱图是一种用于可视化信号频谱的图形表示方法。它显示了信号在不同频率上的能量分布，通常以频率为横轴，以信号强度或能量为纵轴。频谱图可用于分析音频、无线通信、雷达等领域中的信号特性。

快速傅里叶变换是一个强大的工具，它允许我们分析信号的频率成分，但是如果我们信号的频率成分随时间变化怎么办？大多数音频信号（如音乐和语音）都是这种情况。这些信号被称为非周期信号。我们需要一种方法来表示这些信号的频谱，因为它们随时间变化。通过在信号的几个窗口段上执行FFT来计算多个频谱，它被称为短时傅里叶变换。?FFT是在信号的重叠窗口段上计算的，我们得到所谓的频谱图。

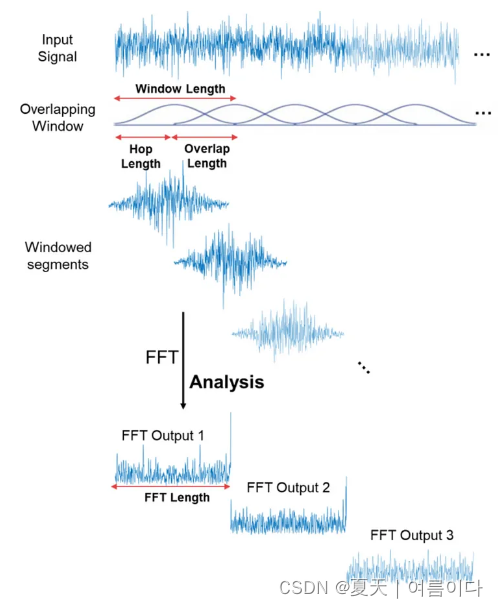
经过处理后生成频谱图

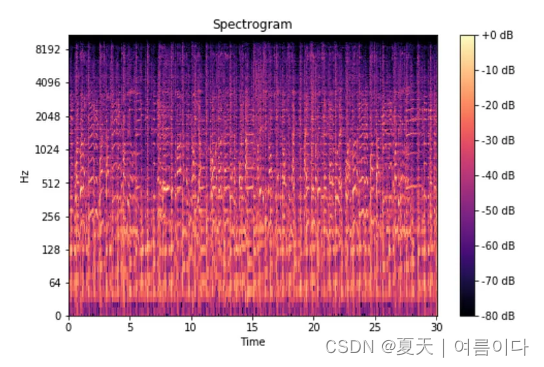
• 横轴（X轴）：频率轴

  横轴表示信号的频率范围，通常以赫兹（Hz）为单位。低频在图的左侧，高频在图的右侧。

• 纵轴（Y轴）：振幅或功率

  纵轴通常表示信号的振幅、功率或能量，取决于具体的应用。在一些图中，可以使用线性或对数刻度来表示振幅。

• 颜色：表示信号强度

  频谱图中的颜色深浅一般用于表示信号的强度，深色通常表示较高的能量，浅色表示较低的能量。有时，也可以使用不同颜色来区分不同的信号或频带。

• 时间维度（如果有）：时频图

  有些频谱图还包括时间维度，形成了时频图。时频图可以显示信号在时间和频率上的变化，适用于分析非稳态信号（随时间变化的信号）。

• 窗函数和FFT（快速傅里叶变换）

  在频谱图的制作过程中，通常会使用窗函数对信号进行分段，然后对每个窗口应用FFT来获取频域信息。FFT是一种计算傅里叶变换的高效算法。

• 谱线和谱带

  频谱图上的谱线表示信号在不同频率上的分量，而谱带表示每个频率范围内的信号能量。

3.梅尔量表

?我们可以很容易地分辨出 500 和 1000 Hz 之间的区别，但我们几乎无法分辨出 10,000 和 10,500 Hz 之间的区别，即使两对之间的距离相同。

1937年，史蒂文斯，福克曼和纽曼提出了一个音高单位，使得相等的音高距离听起来对听众来说同样遥远。这称为梅尔量表。?我们对频率执行数学运算以将它们转换为 mel 刻度。

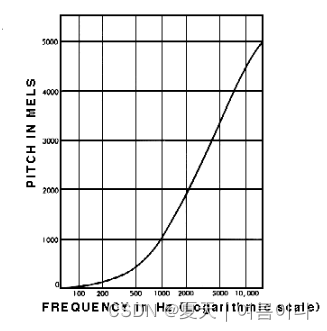
4.梅尔倒谱系数（Mel-frequency Cepstral Coefficients, MFCC）

概念

• MFCC 是梅尔频谱图的一种紧凑的表示形式，主要用于语音识别和音频特征提取。它是梅尔频谱图上的系数，通常选择前13个或更多的系数作为特征。

处理步骤：

• 从梅尔频谱图中选择一定数量的系数，通常通过离散余弦变换（DCT）进行。
• 取对数，然后应用离散余弦变换，最终得到MFCC。

特点：

• MFCC提供了音频信号在梅尔刻度上的重要信息，同时通过DCT，使得它们更加紧凑且不相关，适用于机器学习算法的输入。

梅尔频谱图(mel-spectrogram)

梅尔频谱图是将频率转换为梅尔刻度的频谱图。

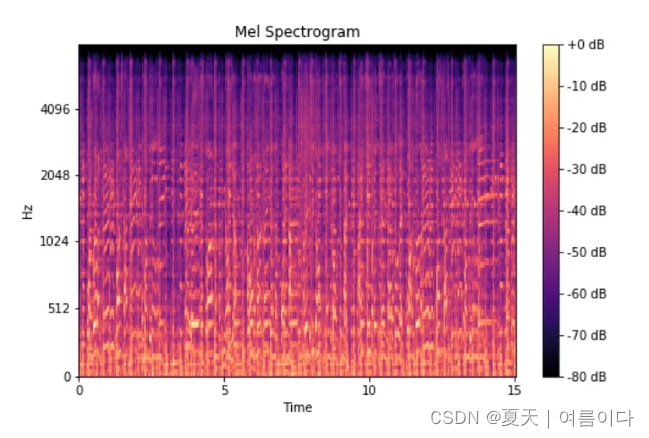
概念：

• 梅尔频谱图是对音频信号进行频域分析的一种方法。它与常规的频谱图类似，但使用了梅尔刻度（Mel scale），该刻度更符合人类听觉的感知。梅尔刻度在低频部分更密集，在高频部分更稀疏，与人类听觉对音调的感知更相符。

处理步骤：

• 将音频信号分帧，对每一帧进行傅里叶变换，得到能量谱。
• 将能量谱映射到梅尔刻度上，通常使用三角滤波器组（Mel滤波器组）来实现这一映射。
• 对每个滤波器的能量进行对数运算，得到梅尔频谱图。

特点：

• 梅尔频谱图在频域上更符合人类听觉的感知，能够更好地反映音频信号的重要特征。
• 通常使用对数尺度，使得相对较小的能量变化更加显著。

Mel-spectogram feature

机器学习的时候，每一个音频段可用对应的mel-spectogram表示，每一帧对应的某个频段即为一个feature。

实际操作中，每个音频要采用同样的长度，feature数量才是相同的。通常还要进行归一化，即每一帧的每个元素要减去该帧的平均值，以保证每一帧的均值均为0。
?

总结

1.音频信号处理

得到一个音频，以数字方式表示音频信号。然后使用快速傅里叶变换将音频信号从时域映射到频域，并在音频信号的重叠窗口段上执行此操作。

将y轴（频率）转换为对数刻度，将颜色维度（振幅）转换为分贝以形成频谱图。

将y轴（频率）映射到mel刻度上以形成mel频谱图。

2.MFCC和梅尔语谱图(Mel spectrogam)的区别

• 表示形式：

  • 梅尔频谱图是一个矩阵，每一行表示一个频带，每一列表示一个时间窗口。
  • MFCC是从梅尔频谱图中提取的系数，可以看作是对梅尔频谱的降维表示。

• 应用：

  • 梅尔频谱图通常用于可视化音频信号的频域分布。
  • MFCC通常用于作为语音信号的特征向量，用于语音识别等任务。

• 维度：

  • 梅尔频谱图的维度与原始信号长度和频带数相关。
  • MFCC通常选择前13个或更多的系数，因此维度较低，适合作为机器学习模型的输入。

参考文献

【1】?Understanding the Mel Spectrogram | by Leland Roberts | Analytics Vidhya | Medium

【2】Getting to Know the Mel Spectrogram | by Dalya Gartzman | Towards Data Science?

【3】【精选】Mel spectrum梅尔频谱与MFCCs_melspectrum-CSDN博客?

【4】Inverse short-time Fourier transform - MATLAB istft - MathWorks ??

【5】?使用一维卷积计算stft与istft - 知乎 (zhihu.com)

【6】傅里叶变换@（stft和istft）-CSDN博客?

【7】【精选】语音处理/语音识别基础（五）- 声音的音量，过零率，音高的计算_davidullua的博客-CSDN博客

【8】?语音基础知识（附相关实现代码） - 知乎 (zhihu.com)

【9】FFT (nti-audio.com)?