【动态规划】09路径问题_最小路径和_C++(medium)
题目链接:leetcode最小路径和
目录
题目解析:

题目让我们求从左上角到右下角的路径,使得路径上的数字总和为最小
由题可得:
每次只能向下或者向右移动一步
算法原理:
1.状态表示
先创建一个dp表
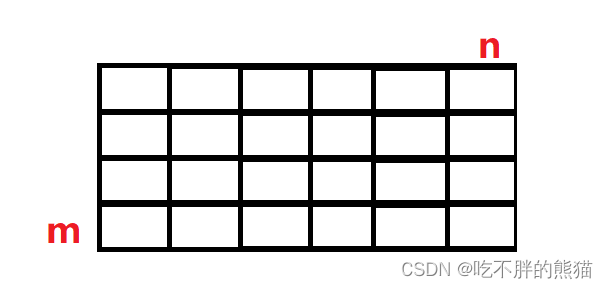
首先先思考dp表里面的值所表示的含义(是什么?)
dp[i][j]表示到达[i][j]路径上的数字总和为最小
这种状态表示怎么来的?
1.经验+题目要求
用之前或者之后的状态,推导出dp[i][j]的值;
根据最近的最近的一步,来划分问题
经验:以i位置为结尾
题目让我们求到达右下角路径上的数字总和为最小,那么这里我们可以dp[i][j]来表示。
所以这里我们用i*j表示右下角位置;
2.状态转移方程
dp[i]等于什么?
因为我们每次只能向下或者向右移动一步
所以到达[i][j]位置有两种情况:
第一种:从[i-1][j]到达i位置
我们这里只要知道到达[i-1][j]路径上的数字总和的最小值,再加上[i]位置的数值(grid[i][j])
就可以得到[i][j]位置路径上的数字总和的最小值(dp[i][j]);
而“到达[i-1][j]路径上的数字总和的最小值”正好是我们的状态表示:dp[i-1][j]
所以这一种情况的状态转移方程为:
dp[i]=dp[i-1][j]+grid[i][j]
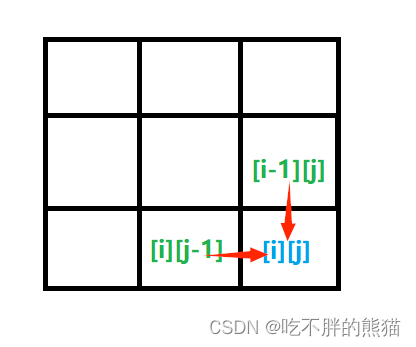
第二种:从[i-1][j]到达i位置
我们这里只要知道到达[i][j-1]路径上的数字总和的最小值,再加上[i]位置的数值(grid[i][j])
就可以得到[i][j]位置路径上的数字总和的最小值(dp[i][j]);
而“到达[i][j-1]路径上的数字总和的最小值”正好是我们的状态表示:dp[i][j-1]
所以这一种情况的状态转移方程为:
dp[i]=dp[i][j-1]+grid[i][j]
总结这两种情况:
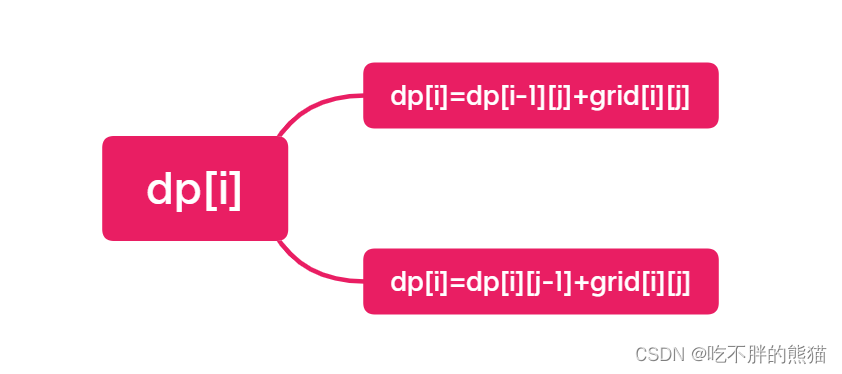
因为题目让我们求的是到达右下角路径上的数字总和为最小
所以这里我们要取这两种情况的最小值
dp[i][j]=min(dp[i-1][j]+dp[i][j-1])+grid[i][j]
3.初始化
(保证填表的时候不越界)
由我们的状态转移方程得:
在0行0列的时候越界,所以我们这里可以在m*n的外围多加1行1列,如图:

还有一个问题是:
我们要拿新增用来初始化的行和列要初始化为几呢?
这里我们需要注意的一点就是在dp[1][1]的时候,路径上的数字总和的最小值就是他本身grid
所以我们只要在dp表里的dp[0][1]、dp[1][0]中任选一个
初始化为cost[0][0]就可以了
其他的地方直接初始化为无穷大值INT_MAX
4.填表顺序
(为了填写当前状态的时候,所需要的状态已经计算过了)
这里所需要的状态是:到达该位置的上面和左边位置的方式
所以填表顺序:
从上到下填写每一行
从左到右填写每一列
5.返回值
(根据题目要求和状态表示)
综上分析:
返回值为:dp[m][n];
编写代码:

class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
//1.创建dp表
//2.初始化
//3.填表
//4.返回结果
int m=grid.size();
int n=grid[0].size();
vector<vector<int>> dp(m+1,vector<int>(n+1,INT_MAX));
dp[0][1]=0;
for(int i=1;i<m+1;i++)
for(int j=1;j<n+1;j++)
dp[i][j]=min(dp[i][j-1],dp[i-1][j])+grid[i-1][j-1];
return dp[m][n];
}
};本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 使用Python合并PPT文件
- 2023读书笔记55|微读699元的书读后感——《走进美加风光摄影集》
- 【C语言】排序(三)(快速排序:递归与非递归实现)
- 【Java基础】BIO/NIO/AIO的详细介绍与比较区分
- 网络安全(黑客)——自学2024
- PRVF-4007 : User equivalence check failed for user “grid“
- 通用异构参数服务器技术
- 13.适配器模式
- springboot连接oracle报错ORA-12505解决方案
- idea Spring Boot项目使用JPA创建与数据库链接