12.23用树、DAG表示表达式

有向图的顶点的度等于该顶点的入度与出度之和。

因此对于邻接表，某个顶点的链表为空，该顶点出度为0。

对于逆邻接表，某个顶点的链表为空，该顶点入度为0。

一个有向图D=(V, A)满足什么条件是V到V的一个映射的图？

A对任意 v∈V, od(v)=1;

从Vi到Vj的映射，是指对于V中的每一个元素i，V中都有一个唯一的元素j与之对应，也就是 i--->j 唯一，出度=1。就是说要么一对一，要么一对多，要形成唯一确定的关系，每个点都只能由一个点确定

入度为1，正是DAG的特点，

即理解为只能由一个唯一的点确定，或者前驱只有一个

拓扑排序，事件的先后关系，正是体现在唯一的紧邻前驱上

用树、DAG表示表达式

用有向无环图描述表达式 (A+B)*((A+B)/A), 至少需要顶点的数目为 ( 5)

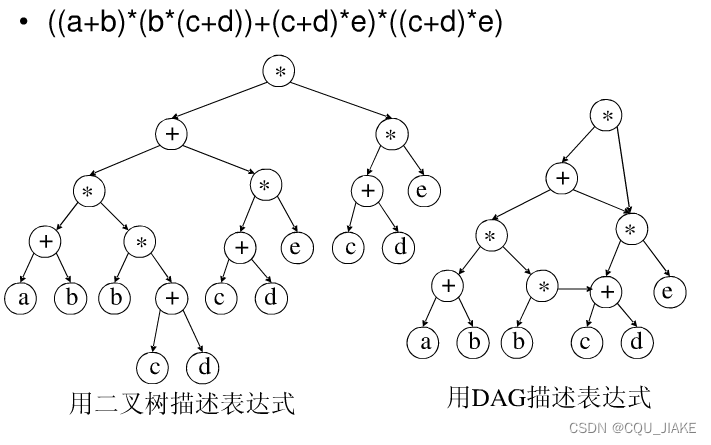
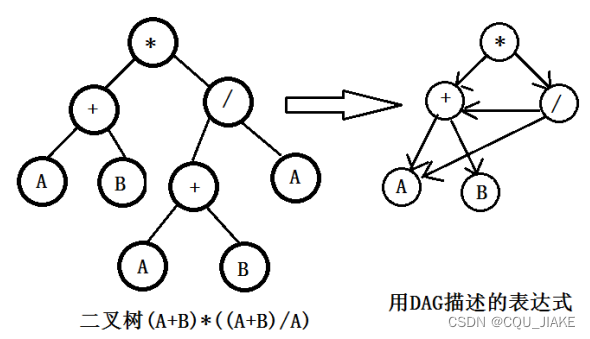
用DAG表述，首先是要得到二叉树的表示，然后采用拓扑排序的方法，结合、化简掉中间过程中出现的一些部分，从而实现化简.实际就是一个去重的过程

大顶堆中除了堆顶元素是最大值，其余元素的顺序都是无法确定的。

堆排序的时间，主要由建立初始堆和反复重建堆这两部分的时间开销构成，它们均是通过调用Heapify实现的。时间复杂度O(n*logn) 如果从底部最后的父节点开始建堆，那么我们可以大概算一下： 假如有N个节点，那么高度为H=logN，最后一层每个父节点最多只需要下调1次，倒数第二层最多只需要下调2次，顶点最多需要下调H次，而最后一层父节点共有2^(H-1)个,倒数第二层公有2^(H-2),顶点只有1(2^0)个，所以总共的时间复杂度为s = 1 * 2^(H-1) + 2 * 2^(H-2) + ... + (H-1) * 2^1 + H * 2^0 将H代入后s= 2N - 2 - log2(N)，近似的时间复杂度就是O(N)。

如果堆的有序状态因为某个节点变得比它的父节点更大而打破，那么就需要通过交换它和它的父节点来修复堆。从最后一个非叶结点逐渐往上浮，直到有序。

根元素为最小值的二叉堆：

插入节点时间复杂度为O(log n)

删除节点时间复杂度为O(log n)

查询最小元素的复杂度是o(1)

合并两个堆的复杂度是o(lgn)

对于有n(n>3)个不重复元素的大顶堆，下标为n-2的元素和下标为n-1的元素的大小关系是()

因为只有堆顶元素是确定的最大值，对于末尾元素，只有小于父节点这一个条件；因此它们的大小关系无法确定。

创建堆的基本思想：先把无序的关键字按顺序构造成完全二叉树，从最后一个分支节点开始往前，不断地利用筛选算法，将一棵棵子树调整为一个堆，一直进行到完全二叉树的根节点为止。