Kruskal算法求最小生成树（并查集讲解）

这个跟前者Prim算法目前我学来的都是为了求最小生成树，不过在看y神的视频讲解后发现还是需要一些前置知识的

前置知识

并查集

概念

并查集是一种树型的数据结构，用于处理一些不相交集合的合并及查询问题。

并查集的思想是用一个数组表示了整片森林（parent），树的根节点唯一标识了一个集合，我们只要找到了某个元素的的树根，就能确定它在哪个集合里

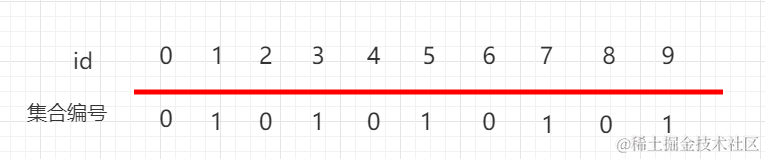
如上图?0-4?下面都是?0，5-9?下面都是?1，表示?0、1、2、3、4?这五个元素是相连接的，5、6、7、8、9?这五个元素是相连的。

再如上图?0、2、4、6、8?下面都是?0?这个集合，表示?0、2、4、6、8?这五个元素是相连接的，1、3、5、7、9?下面都是?1?这个集合，表示?0，1、3、5、7、9?这五个元素是相连的

以上知识应该能了解并查集究竟是什么，它主要支持两种操作：查找（Find）和合并（Union）。并查集常用于解决一些集合划分和连接性的问题，例如连通性判断、最小生成树算法中的 Kruskal 算法等

步骤

并查集通过维护一棵树结构，其中每个节点表示一个元素，树的根节点表示该集合的代表元素。通过合并集合时，将其中一个集合的根节点连接到另一个集合的根节点上，实现集合的合并。路径压缩是一种优化技术，通过在Find操作时将节点直接连接到根节点，缩短树的高度，提高查询效率

1. 初始化：对于每个元素，初始时将其视为一个独立的集合
2. Find 操作：通过递归或迭代的方式找到当前元素所在集合的根节点
3. Union 操作：找到两个元素所在集合的根节点，然后将其中一个根节点的父节点指向另一个根节点，实现集合的合并

public class UnionFind {
    private int[] parent;

    public UnionFind(int n) {
        parent = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i; // 初始化每个元素为独立的集合
        }
    }

    public int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]); // 路径压缩
        }
        return parent[x];
    }

    public void union(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            parent[rootX] = rootY; // 合并集合
        }
    }
}

主要应用在：

1. 连通性判断：判断两个元素是否属于同一集合。
2. 最小生成树算法：如 Kruskal 算法。
3. 图的动态连通性：在图的动态变化过程中判断两个节点是否连通

题目

给定一个?n?个点?m?条边的无向图，图中可能存在重边和自环，边权可能为负数。

求最小生成树的树边权重之和，如果最小生成树不存在则输出?impossible。

给定一张边带权的无向图?G=(V,E)，其中?V?表示图中点的集合，E?表示图中边的集合，n=|V|，m=|E|

由?V?中的全部?n?个顶点和?E?中?n?1?条边构成的无向连通子图被称为?G?的一棵生成树，其中边的权值之和最小的生成树被称为无向图?G?的最小生成树。

输入格式

第一行包含两个整数?n?和?m

接下来?m?行，每行包含三个整数?u,v,w，表示点?u?和点?v?之间存在一条权值为?w?的边。

输出格式

共一行，若存在最小生成树，则输出一个整数，表示最小生成树的树边权重之和，如果最小生成树不存在则输出?impossible。

数据范围

• 1≤n≤105
• 1≤m≤2?105
• 图中涉及边的边权的绝对值均不超过1000

输入样例：

4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4

输出样例：

6

代码与解析

1. 排序边： 将所有边按照权值从小到大进行排序。
2. 初始化并查集： 初始化一个并查集，每个节点初始时属于独立的集合。
3. 遍历边： 按照排序后的顺序，依次考虑每一条边。对于每条边，判断其两个节点是否属于同一个集合，如果不是，则将它们合并，并将这条边加入最小生成树。
4. 判断生成树是否完整： 最终生成树的边数应该为n-1，其中n为节点数。如果生成树边数小于n-1，则说明无法构成最小生成树

import java.util.Arrays;
import java.util.Scanner;

public class KruskalMST {
    static class Edge implements Comparable<Edge> {
        int a, b, w;

        public Edge(int a, int b, int w) {
            this.a = a;
            this.b = b;
            this.w = w;
        }

        @Override
        public int compareTo(Edge other) {
            return Integer.compare(this.w, other.w);
        }
    }

    static int n, m;
    static int[] p;

    public static int find(int x) {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    public static int kruskal(Edge[] edges) {
        Arrays.sort(edges);

        for (int i = 1; i <= n; i++) p[i] = i; // 初始化并查集

        int res = 0, cnt = 0;
        for (Edge edge : edges) {
            int a = edge.a, b = edge.b, weight = edge.w;

            a = find(a);
            b = find(b);
            if (a != b) {
                p[a] = b;
                res += weight;
                cnt++;
            }
        }

        if (cnt < n - 1) return Integer.MAX_VALUE; // 说明无法构成生成树
        return res;
    }

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        n = in.nextInt();
        m = in.nextInt();
        p = new int[n + 1];

        Edge[] edges = new Edge[m];
        for (int i = 0; i < m; i++) {
            int a = in.nextInt();
            int b = in.nextInt();
            int w = in.nextInt();
            edges[i] = new Edge(a, b, w);
        }

        int result = kruskal(edges);

        if (result == Integer.MAX_VALUE) {
            System.out.println("impossible");
        } else {
            System.out.println(result);
        }
    }
}