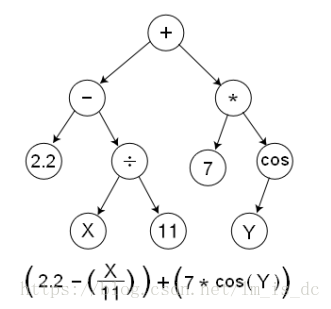
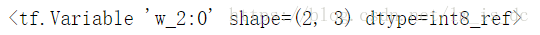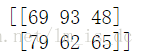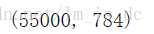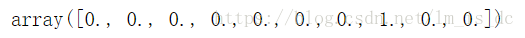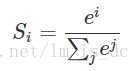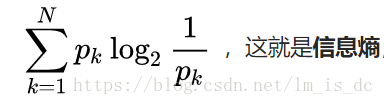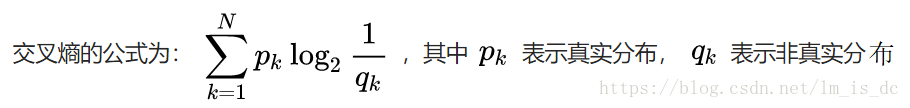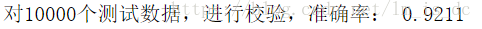教你如何使用TensorFlow框架

一、简介

? TensorFlow是谷歌基于DistBelief进行研发的第二代人工智能学习系统，其命名来源于本身的运行原理。

? Tensor（张量）意味着N维数组，Flow（流）意味着基于数据流图的计算，TensorFlow为张量从流图的一端流动到另一端的计算过程。

? TensorFlow是将复杂的数据结构传输至人工智能神经网中进行分析和处理过程的系统。

TensorFlow可被用于语音识别和图像识别等多项机器学习和深度学习领域，对2011年开发的深度学习基础架构DistBelief进行了各方面的改进，它可在小到一部智能手机、大到数千台数据中心服务器的各种设备上运行。

? TensorFlow是开源的，任何人都可以用。

? 网站：http://playground.tensorflow.org

? 支持CNN（卷积神经网络）、RNN（循环神经网络）和LSTM（长短期记忆网络）算法，是目前在 Image，NLP 最流行的深度神经网络模型.

二、优点

TensorFlow优点：

• 基于Python，写的很快并且具有可读性。
• 在CPU或GPU系统上的都可运行。
• 代码编译效率较高。
• 社区发展的非常迅速并且活跃。
• 能够生成显示网络拓扑结构和性能的可视化图。

三、原理

TensorFlow原理：
TensorFlow是用数据流图(data flow graphs)技术来进行数值计算的。
数据流图是描述有向图中的数值计算过程。
有向图中，节点通常代表数学运算，边表示节点之间的某种联系，它负责传输多维数据(Tensors)。

四、使用

###1、TensorFlow使用

? 使用图(graph)来表示任务
在被称之为会话(Session)的上下文(context)中执行图
使用tensor表示数据
通过变量(Variable)维护状态f(x) = w*x + b
使用feed和fetch可以为任意操作(arbitrary operation)赋值或者从其中获取数据。

2、下载

在管理员模式下cmd窗口中执行：

pip install tensorflow

3、第一个tf程序

导包

# 导包
import tensorflow as tf
import numpy as np
from IPython.display import display

定义常量

# 定义常量
a = tf.constant(np.random.randint(0,100,size=(3,4)))
b = tf.constant(3.14)
s = tf.constant('hello world')
display(a,b,s)
# tensor张量-------> 数据，类比ndarray

定义变量

w = tf.Variable(np.random.randint(0,100,size=(2,3)),
               dtype=tf.int8,  #数据类型
               name='w'  #变量命名，可省略
               )
w

创建会话

sess = tf.Session()

关闭会话

sess.close()

使用会话运行graph

一般使用with语句来创建会话，这样就不用手动关闭会话，with语句会自动关闭会话。

with tf.Session() as sess:
    ret = sess.run(fetches=[a,b,s])
    print(ret)

with tf.Session() as sess:
    # 如果要使用变量，需要进行初始化
    sess.run(tf.global_variables_initializer())
    print(sess.run(w))

4、加减乘除

#加减乘除
a = tf.constant(100,dtype=tf.float16)
b = tf.constant(5,dtype=tf.float16)
#加
c = a + b
d = tf.add(a,b)
#减
e = tf.subtract(a,b)
#乘
f = tf.multiply(a,b)
#除
h = tf.div(a,b)

with tf.Session() as sess:
    print(sess.run([a,b,c,d,e,f,h]))

矩阵乘法

a = tf.constant(np.random.randint(0,10,size = (2,3)))

b = tf.constant(np.random.randint(0,10,size = (3,2)))
#矩阵乘法
m = tf.matmul(a,b)
with tf.Session() as sess:
    print(sess.run([a,b]))
    print(sess.run(m))

降维加法

a = tf.constant(np.random.randint(0,10,size = (4,5)))
#axis=1,列相加
#比如第一个数26 = 8+5+4+8+1
b = tf.reduce_sum(a,axis = 1)

with tf.Session() as sess:
    print(sess.run(a))
    print('-----------------------------')
    print(sess.run(b))

a = tf.constant(np.random.randint(0,10,size = (4,5)))
#axis=0,行相加
#比如第一个数25 = 3+6+8+8
b = tf.reduce_sum(a,axis = 0)

with tf.Session() as sess:
    print(sess.run(a))
    print('-----------------------------')
    print(sess.run(b))

5、placeholder占位符

placeholder：可以先定义矩阵的维度，不必赋初值，在具体的运算时再赋值，定义的变量可以多次赋值。

#占位符  placeholder
#定义一个[None,None]的矩阵和[3,None]的矩阵
#矩阵行和列可以不具体指定，里面的元素值也可以不给
a = tf.placeholder(dtype=tf.float32,shape=[None,None])
b = tf.placeholder(dtype=tf.float32,shape=[3,None])
m = tf.matmul(a,b)
with tf.Session() as sess:
    a1 = np.random.randint(0,10,size = (2,3))
    b1 = np.random.randint(0,10,size = (3,1))
    print('a=',a1)
    print('b=',b1)
    print('a和b的矩阵乘法=',
        sess.run(
            m,
            feed_dict={       #给变量赋值
               a:a1,
               b:b1
            }
        )
    )

五、使用TensorFlow实现线性回归

普通线性回归

from sklearn.linear_model import LinearRegression
# 原理：最小二乘法
# (f(x) - y)**2.sum()

#导包

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

#生成训练数据
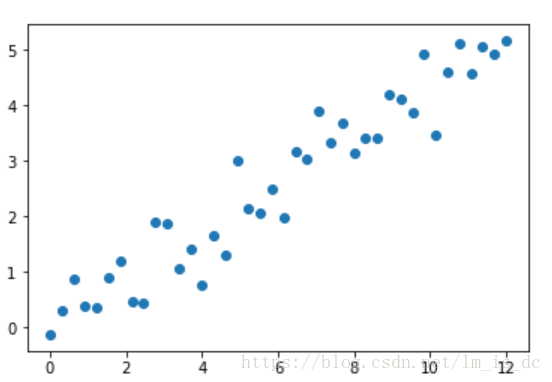
X = np.linspace(0,12,40)
y = np.linspace(0,5,40)
#加噪声
y += np.random.randn(40)*0.5
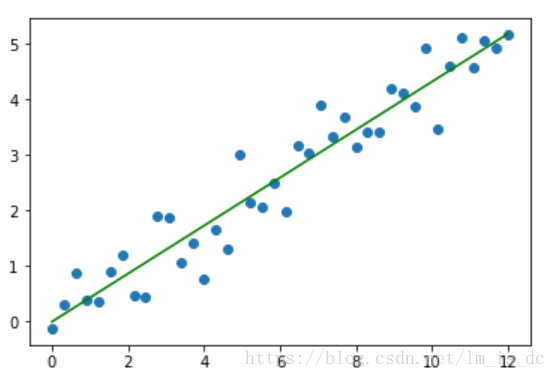
plt.scatter(X,y)

lrg = LinearRegression()
#训练数据要是二维数组
lrg.fit(X.reshape(-1,1),y)
#斜率
w_ = lrg.coef_
#截距
b_ = lrg.intercept_

#绘制回归曲线
plt.scatter(X,y)

x1 = np.linspace(0,12,300)
y1 = w_*x1 + b_
plt.plot(x1,y1,color='green')

使用TensorFlow实现

导包

#导包
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

#绘图时可以显示中文
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False

获取数据

#使用tensorflow

#生成训练数据
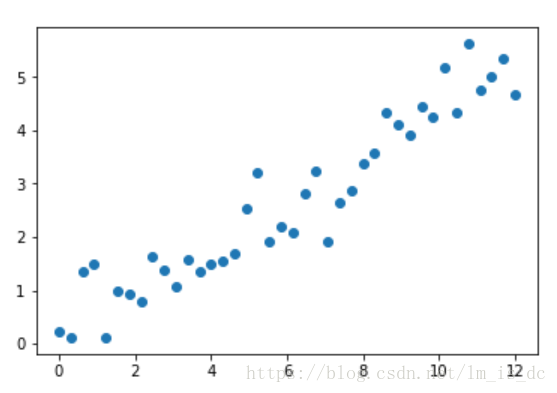
X_train = np.linspace(0,12,40)
y_train = np.linspace(0,5,40)
#加噪声
y_train += np.random.randn(40)*0.5
plt.scatter(X_train,y_train)

定义TensorFlow参数：X，Y，W，b

#定义TensorFlow参数：X，Y，W，b
X = tf.placeholder(dtype=tf.float32,shape=[None,1],name='data')
Y = tf.placeholder(dtype=tf.float32,shape=[None,1],name='target')
#定义两个变量W和b,赋初值
#斜率
W = tf.Variable(np.random.randn(1,1),name='weight',
				dtype=tf.float32)
#截距
b = tf.Variable(np.random.randn(1,1),name='bias',
				dtype=tf.float32)

创建线性模型

#创建线性模型
pred = tf.matmul(X,W) + b

创建均方误差cost (损失函数)

tf.reduce_sum() 降维加法

pred = [[p1],[p2],[p3]……]

Y = [[y1],[y2],[y3],……]

(pred-Y) 相同的位置进行相减

有40个点，除以40求平均值.

cost = tf.reduce_sum(tf.pow(tf.subtract(pred,Y),2))/40

也可以写成:

cost = tf.reduce_mean(tf.pow(tf.subtract(pred,Y),2))

创建梯度下降优化器optimizer

使用梯度下降方式去找损失函数cost的最小值.

函数的导数就是函数的梯度.

梯度下降的学习率learning_rate=0.01.

optimizer = tf.train.GradientDescentOptimizer(0.01).minimize(cost)

TensorFlow进行初始化，并进行运算

#定义训练次数
epoches = 1000
with tf.Session() as sess:
    #变量初始化
    sess.run(tf.global_variables_initializer())
    #循环
    for i in range(epoches):
        opt,c = sess.run([optimizer,cost],
        		# 给占位符设置数据
                        feed_dict={
                            X:X_train.reshape(-1,1),
                            Y:y_train.reshape(-1,1)
                        }
                        )
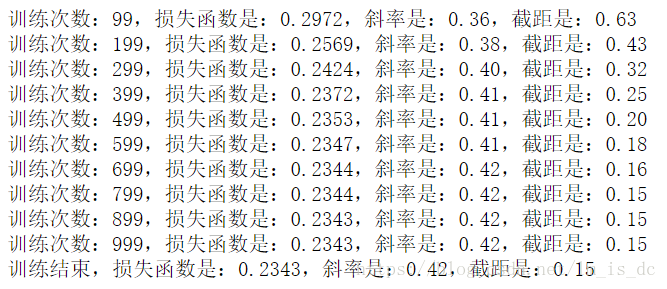
        #100次循环打印输出一次
        if (i+1)%100 == 0:
            w_ = sess.run(W)
            b_ = sess.run(b)
            print('训练次数：%d，损失函数是：%0.4f，斜率是：%0.2f，截距是：%0.2f'%(i,c,w_,b_))
            
    c = sess.run(cost,feed_dict={X:X_train.reshape(-1,1),Y:y_train.reshape(-1,1)})
    w_ = sess.run(W)
    b_ = sess.run(b)
    print('训练结束，损失函数是：%0.4f，斜率是：%0.2f，截距是：%0.2f'%(c,w_,b_))            

随着训练次数的增大，损失函数在逐渐减小，得到的斜率和截距绘制出的回归曲线就越准确。

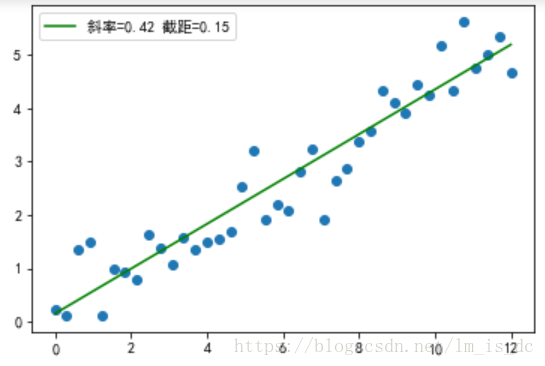
绘制回归曲线

#绘制图形
plt.scatter(X_train,y_train)

x1 = np.linspace(0,12,200)
#绘制回归线
plt.plot(x1,x1*0.42 + 0.15,color = 'green',label='斜率=%0.2f 截距=%0.2f'%(0.42,0.15))
plt.legend()

六、使用TensorFlow实现类逻辑斯蒂回归

导包

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

import tensorflow as tf
#导入手写数字的数据
from tensorflow.examples.tutorials.mnist import input_data

加载数据

加载当前目录下data文件夹中的4个压缩文件

t10k-images-idx3-ubyte.gz

t10k-labels-idx1-ubyte.gz

train-images-idx3-ubyte.gz

train-labels-idx1-ubyte.gz

mnist = input_data.read_data_sets('./data/',one_hot=True)
#mnist

mnist.train.num_examples

mnist中有55000个训练数据。

#二维化的图片数据  原始图像大小28*28
images = mnist.train.images
images.shape

images已经是处理过的二维图片数据，意味着在训练模型时可以直接使用。

#在其它地方的概率为0，下标为7的地方概率为1
# 所以其代表数字7
mnist.train.labels[0]

labels数组中的每一个元素值代表的是概率，哪个下标对应的概率大，这个数组就表示是哪个数字的概率大。

plt.figure(figsize=(1,1))

plt.imshow(images[0].reshape(28,28),cmap = 'gray')

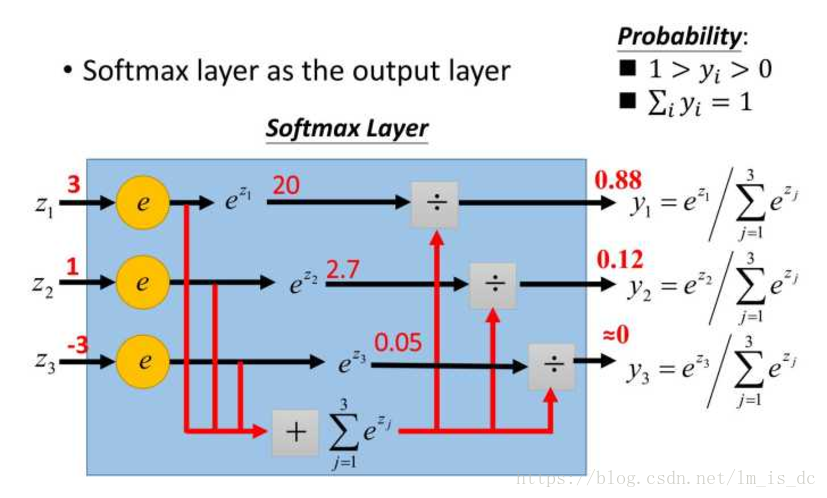
softmax()

softmax用于多分类过程中，它将多个神经元的输出，映射到（0,1）区间内，可以看成概率来理解，从而来进行多分类！

假设我们有一个数组，V，Vi表示V中的第i个元素，那么这个元素的softmax值就是

其它元素的计算如下图：

a = tf.constant([3,1,-3],dtype=tf.float32)
#nn:神经网络的缩写  neural network
#使用softmax函数把元素值映射成0到1的概率
b = tf.nn.softmax(a)

with tf.Session() as sess:
    print(sess.run(b))
    print(sess.run(b).sum())

将原来输出是3,1,-3通过softmax函数一作用，就映射成为(0,1)的值，而这些值的累和为1（满足概率的性质），那么我们就可以将它理解成概率，在最后选取输出结点的时候，我们就可以选取概率最大（也就是值对应最大的）结点，作为我们的预测目标！

【参考：https://www.cnblogs.com/alexanderkun/p/8098781.html】

定义TensorFlow参数：X，Y，W，b

# None 表示任意，表示样本数量
X = tf.placeholder(dtype=tf.float32,shape=[None,784])
# p目标值，真实分布
#数字0到9有10个，于是输出的数组有10列
p = tf.placeholder(dtype=tf.float32,shape=[None,10])

# W代表斜率
#一共有784个特征，所以矩阵X与W相乘时需要784行，
#输出的预测值pred有10列，所以W有10列
#[None,784]*[784,10]   -----> [None,10]
#给变量赋初值为全0的矩阵
W = tf.Variable(np.zeros(shape=(784,10)),dtype=tf.float32)

# 截距 
b = tf.Variable(np.zeros(shape=10),dtype=tf.float32)

创建线性模型

#创建线性模型
pred = tf.matmul(X,W) + b

# 求解出来的pred转换成softmax 概率了
# q是预测出来，非真实分布
q = tf.nn.softmax(pred)

由于预测值是概率发布，所以不能使用均方误差来求解最小的损失函数，在这里需要用到交叉熵作为损失函数。

###使用交叉熵作为损失函数

信息熵公式：

交叉熵公式：

交叉熵，其用来衡量在给定的真实分布下，使用非真实分布所指定的策略消除系统的不确定性所需要付出的努力的大小。

因此，交叉熵越低，这个策略就越好，最低的交叉熵也就是使用了真实分布所计算出来的信息熵，因为此时 ，交叉熵 = 信息熵。这也是为什么在机器学习中的分类算法中，我们总是最小化交叉熵，因为交叉熵越低，就证明由算法所产生的策略最接近最优策略，也间接证明我们算法所算出的非真实分布越接近真实分布。

【参考：https://www.zhihu.com/question/41252833】

求交叉熵代码：

#根据公式求交叉熵
# p*log(1/q)
sub_key = tf.multiply(p,tf.log(1/q))

#求和 
#axis=1 把每一列对应数值取出来相加 得到一维数组A
#比如A[0] = 取出每一列的第一个数相加  
sub_sum = tf.reduce_sum(sub_key,axis=1)

#求均值  A数组是每一个样本的交叉熵，对A求均值
cost = tf.reduce_mean(sub_sum)

# cost = tf.reduce_mean(tf.reduce_sum(tf.multiply(p,tf.log(1/q)),axis = 1))

创建梯度下降优化器optimizer

使用梯度下降方式去找损失函数cost的最小值.

函数的导数就是函数的梯度.

梯度下降的学习率learning_rate=0.01.

#创建梯度下降优化器
optimizer = tf.train.GradientDescentOptimizer(0.01).minimize(cost)

初始化TensorFlow进行运算

# 初始化TensorFlow进行运算

with tf.Session() as sess:
    # 变量初始化
    sess.run(tf.global_variables_initializer())
    
    # 训练55000次，每次取出100个样本
    for i in range(100):
        c_ = 0
        for j in range(550):
            # 每次取100个样本
            X_train,y_train = mnist.train.next_batch(100)
            opt_,c = sess.run([optimizer,cost],
                               feed_dict={
                                  X:X_train,
                                  p:y_train
                               }
                              )
            #对求得损失函数值求和，然后求其均值
            c_ += c
        #求均值
        c_ = c_ / 550
        
        # 每10次循环打印一次
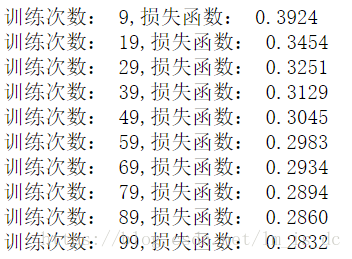
        if (i+1)%10 == 0:
            print('训练次数： %d,损失函数： %0.4f'%(i,c_))
    
    # 保存模型
    saver = tf.train.Saver()
    #模型命名为log_estimator
    saver.save(sess,'./model/like_logistic/log_estimator')

可以看到随着训练次数的增多，损失函数值在减小。

保存模型后，在文件夹下可看到如下文件：

计算准确率

with tf.Session() as sess:
    saver = tf.train.Saver()
    saver.restore(sess,'./model/like_logistic/log_estimator')
    #预测
    y_ = sess.run(q,feed_dict={X:mnist.test.images})
    print(y_.shape)
    # 获取y_中每一行最大的概率
    y_ = tf.argmax(y_,axis=1)
    
    # 获取真实分布中每一行最大的概率
    y_test = tf.argmax(mnist.test.labels,axis=1)
    
    #比较预测值和真实值
    e = tf.equal(y_,y_test)
    
    # 类型转换 True --> 1  False --> 0
    acc = tf.cast(e,dtype=np.float32)
    
    # 求均值
    accuracy = tf.reduce_mean(acc)
    
    print('对10000个测试数据，进行校验，准确率： %0.4f'%(sess.run(accuracy)))