softmax回归+损失函数
本文章借鉴李沐老师动手深度学习,只作为个人笔记.
3.4. softmax回归 — 动手学深度学习 2.0.0 documentation (d2l.ai)
文章目录
前言
经过后面不断学习,我突然发现哪里都有softmax的身影,而且对于softmax回归有助于帮助我们理解神经网络,因为与线性回归一样,softmax回归也是一个单层神经网络,在深度学习中我们也通常在最后使用softmax函数,从而使用交叉熵损失函数,然而pytorch中torch.nn.crossentropyloss()函数,会自动对输入模型的预测值进行softmax。因此在多分类问题中,如果使用nn.CrossEntropyLoss(),则预测模型的输出层无需添加softmax层。
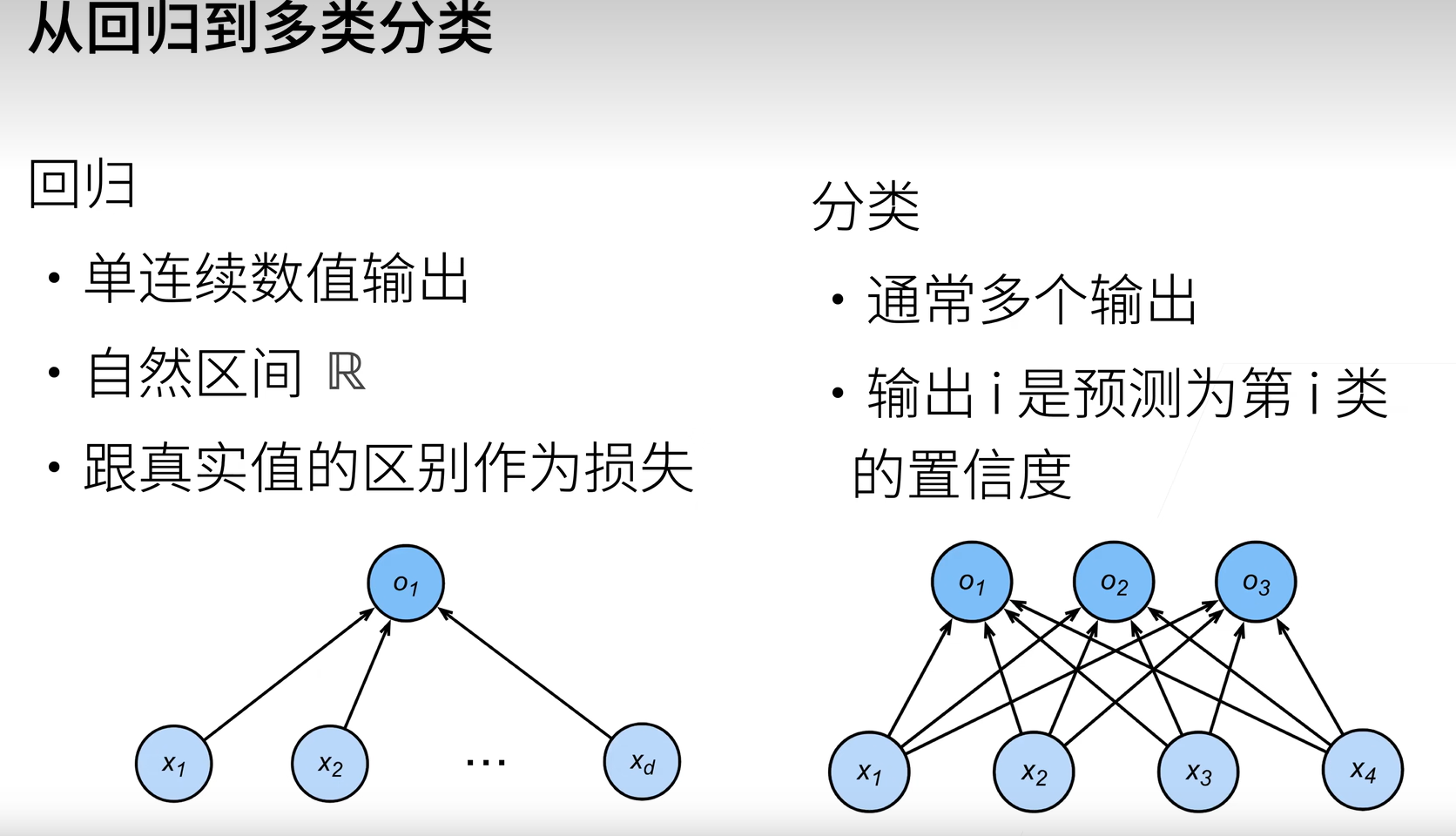
一、回归vs分类
- 回归估计一个连续值.
- 分类预测一个离散类别.
通常,机器学习实践者用分类这个词来描述两个有微妙差别的问题: 1. 我们只对样本的“硬性”类别感兴趣,即属于哪个类别; 2. 我们希望得到“软性”类别,即得到属于每个类别的概率。 这两者的界限往往很模糊。其中的一个原因是:即使我们只关心硬类别,我们仍然使用软类别的模型。
二、分类问题
对于{ 婴儿 , 儿童 , 青少年 ,青年人 , 中年人 , 老年人 }这样一个分类,由于计算无法直接识别字符串,所以就需要对分类类别编码,当然我们可以使用{ 婴儿:0?, 儿童:1 , 青少年:2?,青年人:3 , 中年人:4 , 老年人:5 }这样的数字来代替我们的分类类别,然而这样的编码,会导致1>0这样的问题,然而我们的类别是独立的,所以这样的编码会带来一些问题,那么如何对分类类别进行正确的编码呢?
独热编码(One-Hot Encoding)
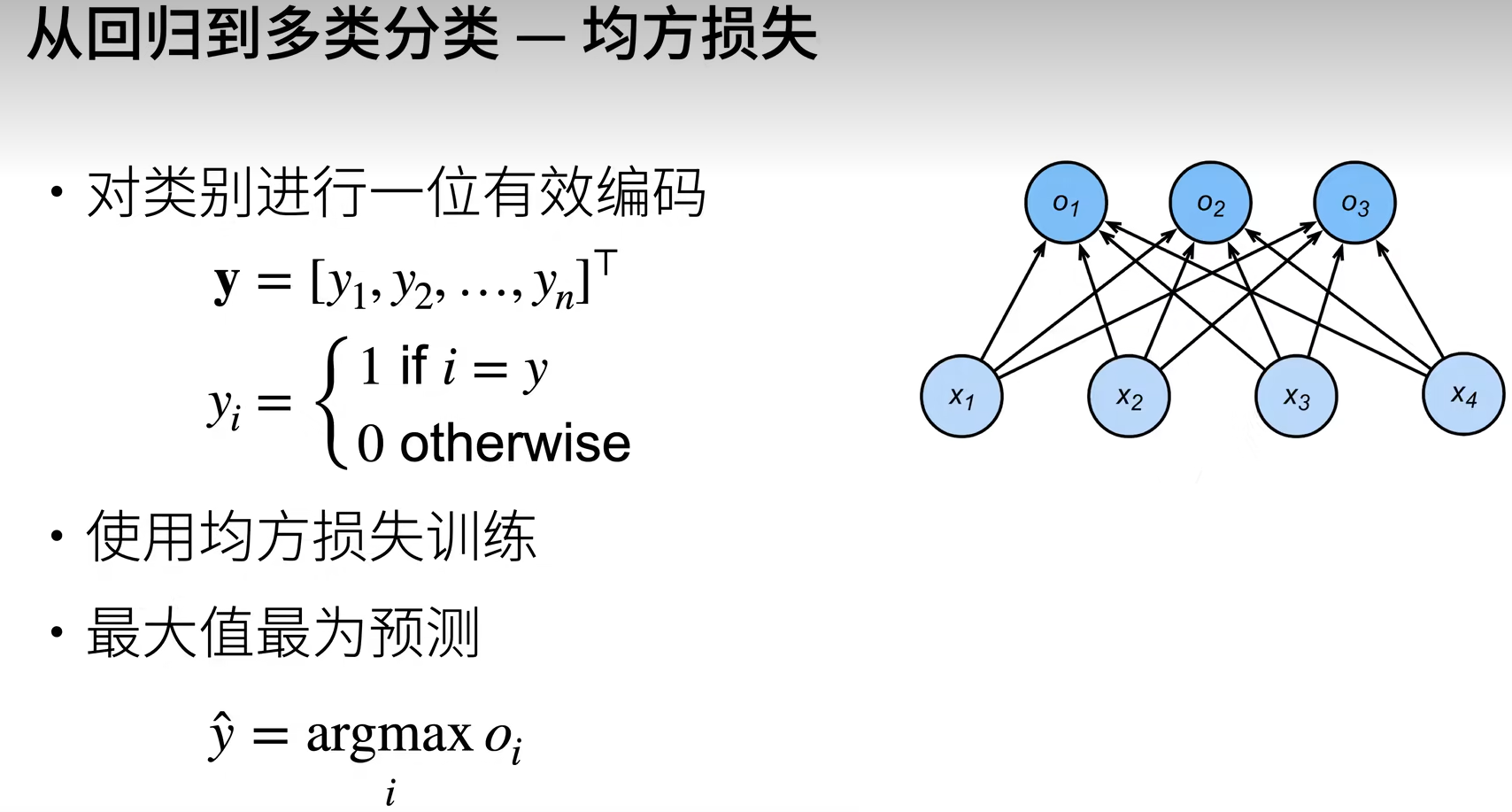
对于{ 婴儿 , 儿童 , 青少年 ,青年人 , 中年人 , 老年人 }分类问题我们采用这样的一种编码形式
- 婴儿[ 1 , 0 ,? 0 ,? 0 , 0]
- 儿童[ 0 , 1 ,? 0,? 0,? 0]
- 青少年[ 0,? 0,? 1 , 0 ,? 0]
- 中年人[ 0,? 0,? 0,? 1,? 0]
- 老年人[ 0,? 0,? 0,? 0,? 1]
学过线性代数可知这几个向量相互正交.
- 优点:独热编码解决了分类器不好处理属性数据的问题,在一定程度上也起到了扩充特征的作用。它的值只有0和1,不同的类型存储在垂直的空间。
- 缺点:当类别的数量很多时,特征空间会变得非常大。在这种情况下,一般可以用PCA来减少维度。而且one hot encoding+PCA这种组合在实际中也非常有用
顺便提一下归一化问题:
- 需要: 基于参数的模型或基于距离的模型,都是要进行特征的归一化。
- 不需要:基于树的方法是不需要进行特征的归一化,例如随机森林,bagging 和 boosting等。
三.网络框架

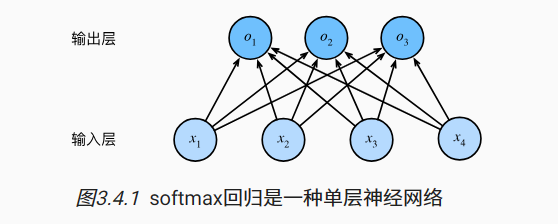
四.softmax运算
1.softmax前提知识
对于上面单层神经网络所得到的输出值
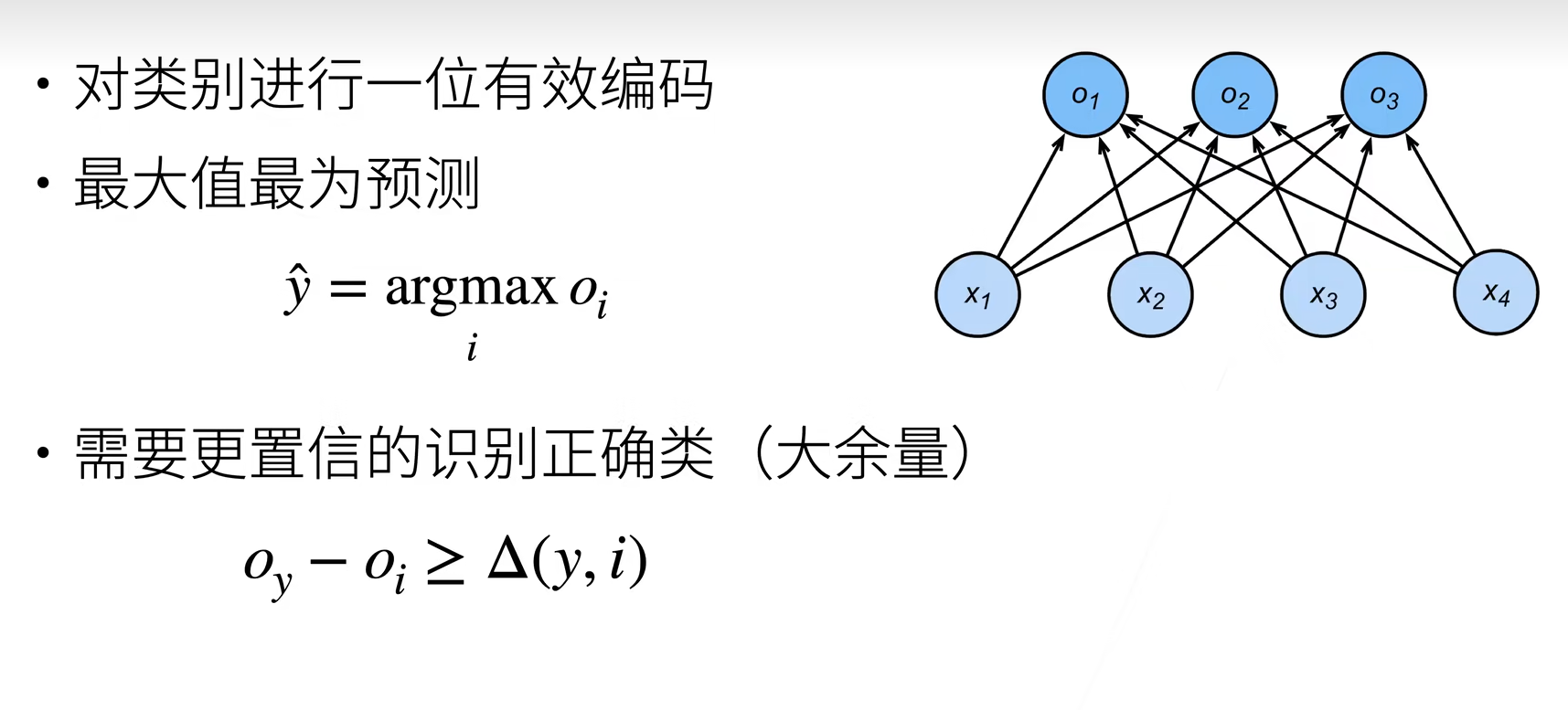
也就是我们输出的结果谁大我们就把测试样本分为哪一类.
例:经过输入一个样本X,输出得到{ 婴儿 , 儿童 , 青少年 ,青年人 , 中年人 , 老年人 }我们所得到的预测为{-1,22,50,34,23}由于青少年的分值较大所以我们认定为该测试样本为青少年.
但是我们想要得到分类类别的概率,如果直接将输出结果O当作我们的概率就会出现问题.
- 一方面,我们没有限制这些输出数字的总和为1。
- 另一方面,根据输入的不同,它们可以为负值。 这些违反了概率基本公理。
要将输出视为概率,我们必须保证在任何数据上的输出都是非负的且总和为1。 此外,我们需要一个训练的目标函数,来激励模型精准地估计概率。
2.softmax函数
?softmax函数能够将未规范化的预测变换为非负数并且总和为1,同时让模型保持 可导的性质。 为了完成这一目标,我们首先对每个未规范化的预测求幂,这样可以确保输出非负。 为了确保最终输出的概率值总和为1,我们再让每个求幂后的结果除以它们的总和。如下式:

y是我们的标签,y(hat)是我们预测标签
尽管softmax是一个非线性函数,但softmax回归的输出仍然由输入特征的仿射变换决定。 因此,softmax回归是一个线性模型(linear model)。

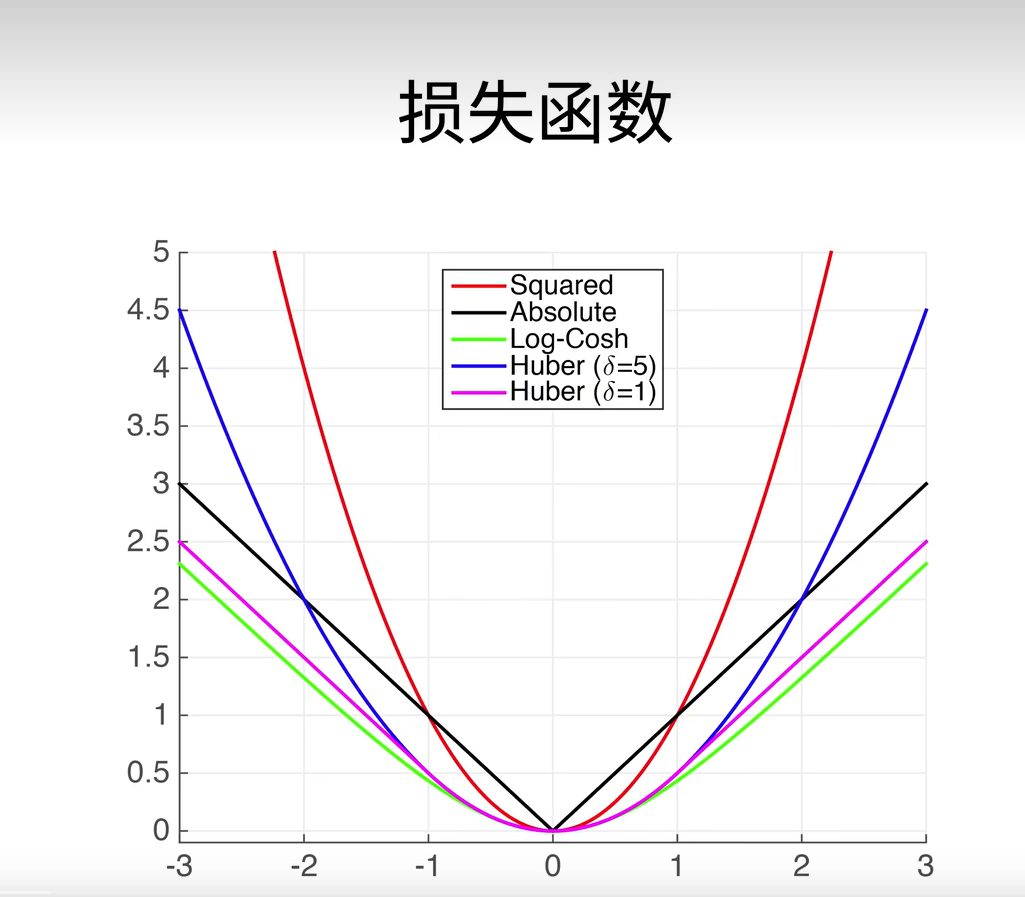
五.简单介绍几个损失函数
L1 loss:
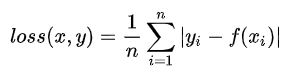
L2 loss:

smooth L1 loss:(Huber's Robust Loss)
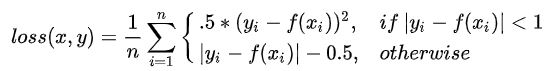
深度学习之L1 loss和L2 loss的区别_l1loss和l2loss的区别-CSDN博客
这里有篇博客详细介绍了各各损失函数的优缺点,我们通常用的L2 loss 比较多.
总结
本文章简单介绍了一下softmax函数,个人认为softmax函数就是可以将输出的结果在扩大个分类样本之间差距的同时又保证了概率基本公理,要熟悉交叉熵损失函数,以及softmax公式用到什么地方,往后深入学习你将会更加理解.
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!