二叉树的四种遍历详解（先序，中序，后序，层次）

目录

引言：

1：先序遍历

2.中序遍历

3.后续遍历

4.层次遍历

先序中序后序例题：

例题1：

例题2：

层次遍历例题：

结语：

---

引言：

二叉树的遍历的概念：二叉树遍历是指按照一定的次序访问二叉树中的所有结点，并且每个结点仅被访问一次的过程。它是二叉树最基本的运算，是二叉树中所有其它运算实现的基础。

为了帮助大家理解各类的遍历过程，下面我给出一个二叉树，下面的各类遍历结果都是根据这张图的图片如下：

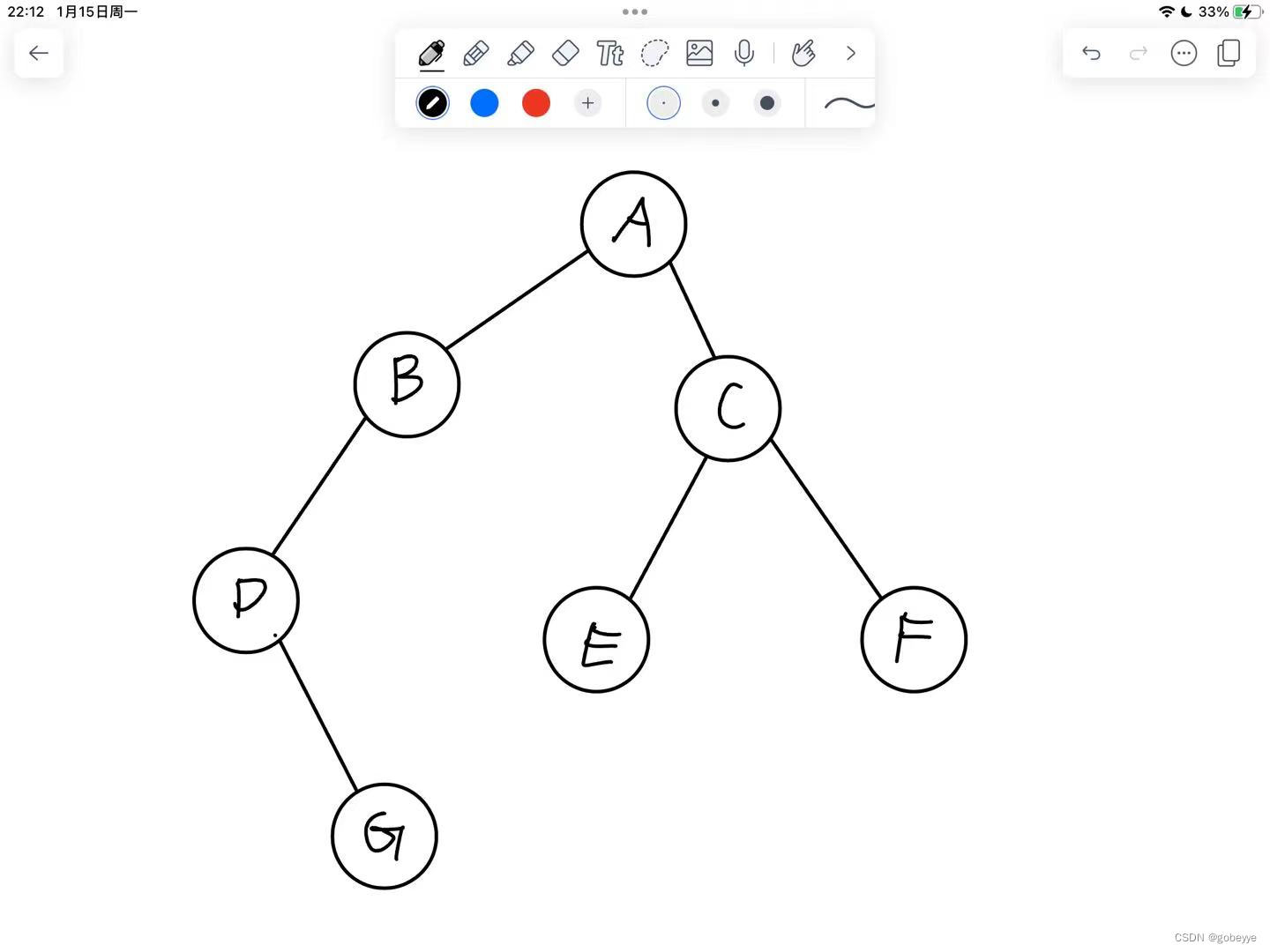
二叉树的遍历各类过程：

先序中序和后序都是利用递归来实现的。

层次遍历使用队列实现的

1：先序遍历

（1）访问跟结点

（2）先序遍历左子树

（3）先序遍历右子树

图所示的二叉树的先序序列位ABDGCEF。

先序的代码：

先访问根节点再访问左子树后右子树。

//先序遍历
void PreOrder(BTNode* b)
{
	if (b != NULL)
	{
		printf("%c ", b->data);
		PreOrder(b->lchild);
		PreOrder(b->rchild);
	}
	return;
}

2.中序遍历

（1）中序遍历左子树

（2）访问跟结点

（3）中序遍历右子树

图所示的二叉树的中序序列位DGBAECF。

中序的代码：

先访问左子树，再访问根结点，最后是右子树。

//中序遍历
void InOrder(BTNode* b)
{
	if (b != NULL)
	{
		InOrder(b->lchild);
		printf("%c ", b->data);
		InOrder(b->rchild);
	}
	return;
}

3.后续遍历

（1）后序遍历左子树

（2）后序遍历右子树

（3）访问根结点

图所示的二叉树的中序序列位GDBEFCA。

后序的代码：

先访问左子树再访问右子树，最后是根结点。

//后序遍历
void PostOrder(BTNode* b)
{
	if (b != NULL)
	{
		PostOrder(b->lchild);
		PostOrder(b->rchild);
		printf("%c ", b->data);
	}
	return;
}

4.层次遍历

（1）访问根节点（第一层）

（2）从左到右访问第二层的所有结点。

（3）从左到右访问第三层的所有结点.....第h层的所有结点。

图所示的二叉树的中序序列位ABCDEFG。

层次的代码：

层次是用队列来实现的下面这个代码只是思路，完整代码后续给出。

那么为什么后想到用队列来实现呢？我们可以观察到，二叉树的层次遍历就是按层次从上到下，每一层从左到右的顺序访问树中的全部结点。故某一层中先访问的结点在下一层中它的孩子也先访问，这样不就和我们的队列特性相符合吗，因此层次遍历算法采用一个队列qu来实现。算法中的队列采用顺序队存储结构。

队列的图片如下：

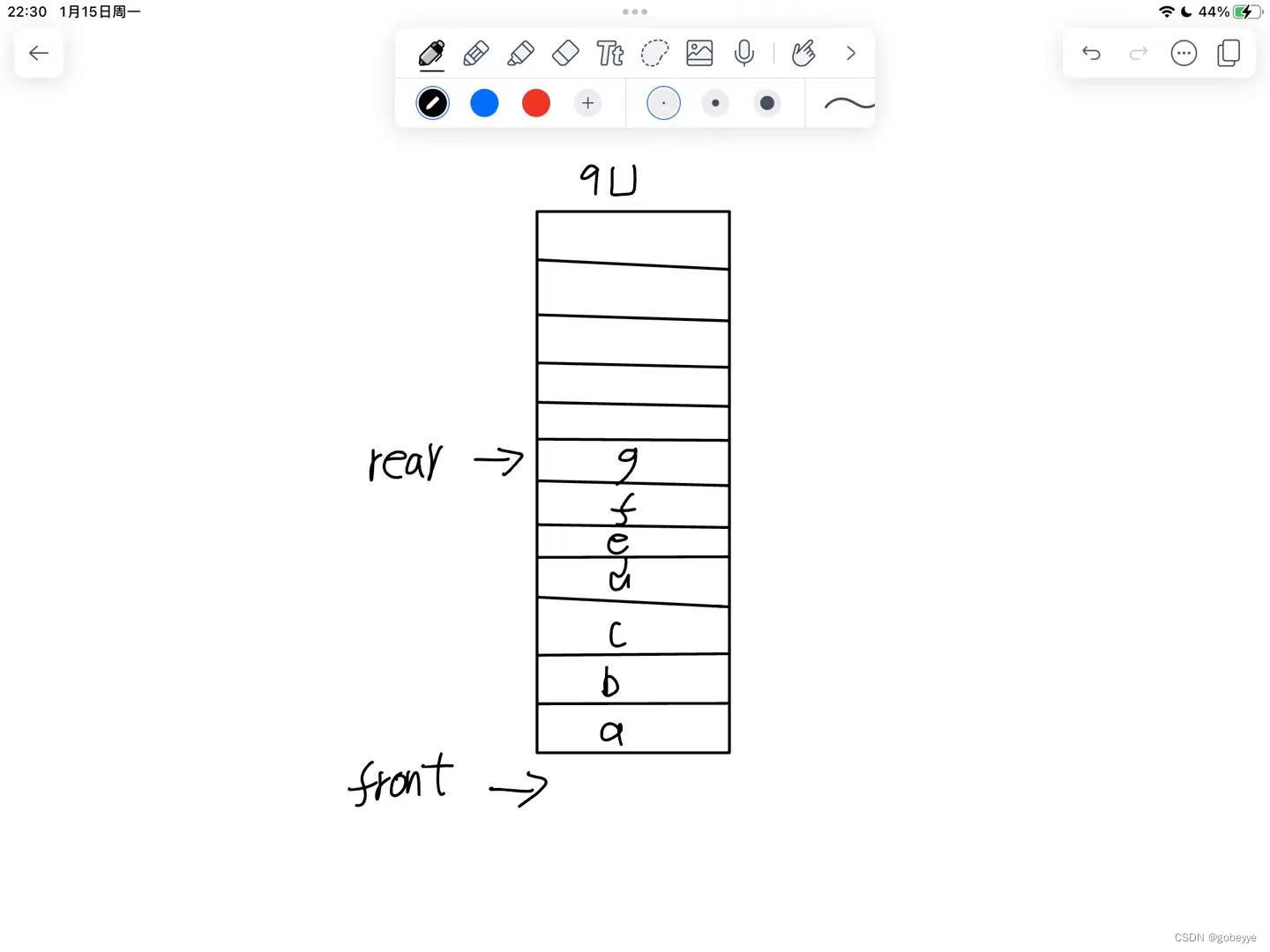
//层次遍历
typedef struct Node
{
	BTNode* data[MaxSize];
	int front, rear;
}SqQueue;
void LevelOrder(BTNode* b)
{
	BTNode* p=NULL;
	SqQueue* qu;
	qu = InitQueue();
	enQueue(qu, b);
	while (!EmptyQueue(qu))
	{
		deQueue(qu, &p);
		printf("%c ", p->data);
		if (p->lchild != NULL)
			enQueue(qu, p->lchild);
		if (p->rchild != NULL)
			enQueue(qu, p->rchild);
	}
	DestroyQueue(qu);
}

以上便是各类遍历的基本思路，下面我会结合一下运用遍历的例题来帮助大家理解，因为文章篇幅有限，故例题只给出实现函数部分，没有给出主函数，特别说明最后面我会给出一个主函数（非常完整），大家例题中的代码都能带进去运行，方便大家调试理解。由于层次遍历和前面三种遍历实现方法不太一样，故下面的例题会分为，前面三种遍历和层次遍历。

先序中序后序例题：

例题1：

设计一个算法，输出一颗给定二叉树的所有结点。

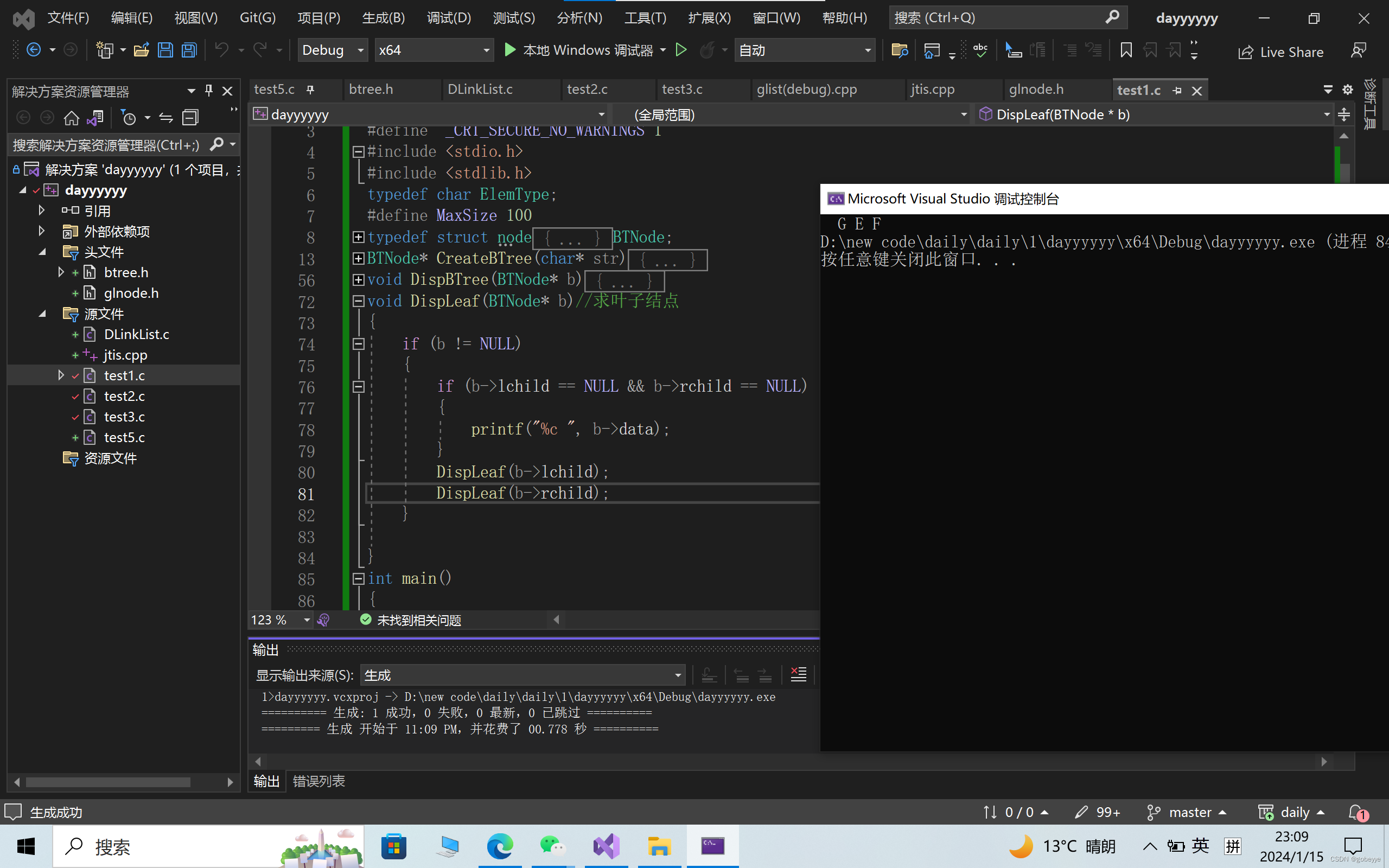
即输出：GEF结点

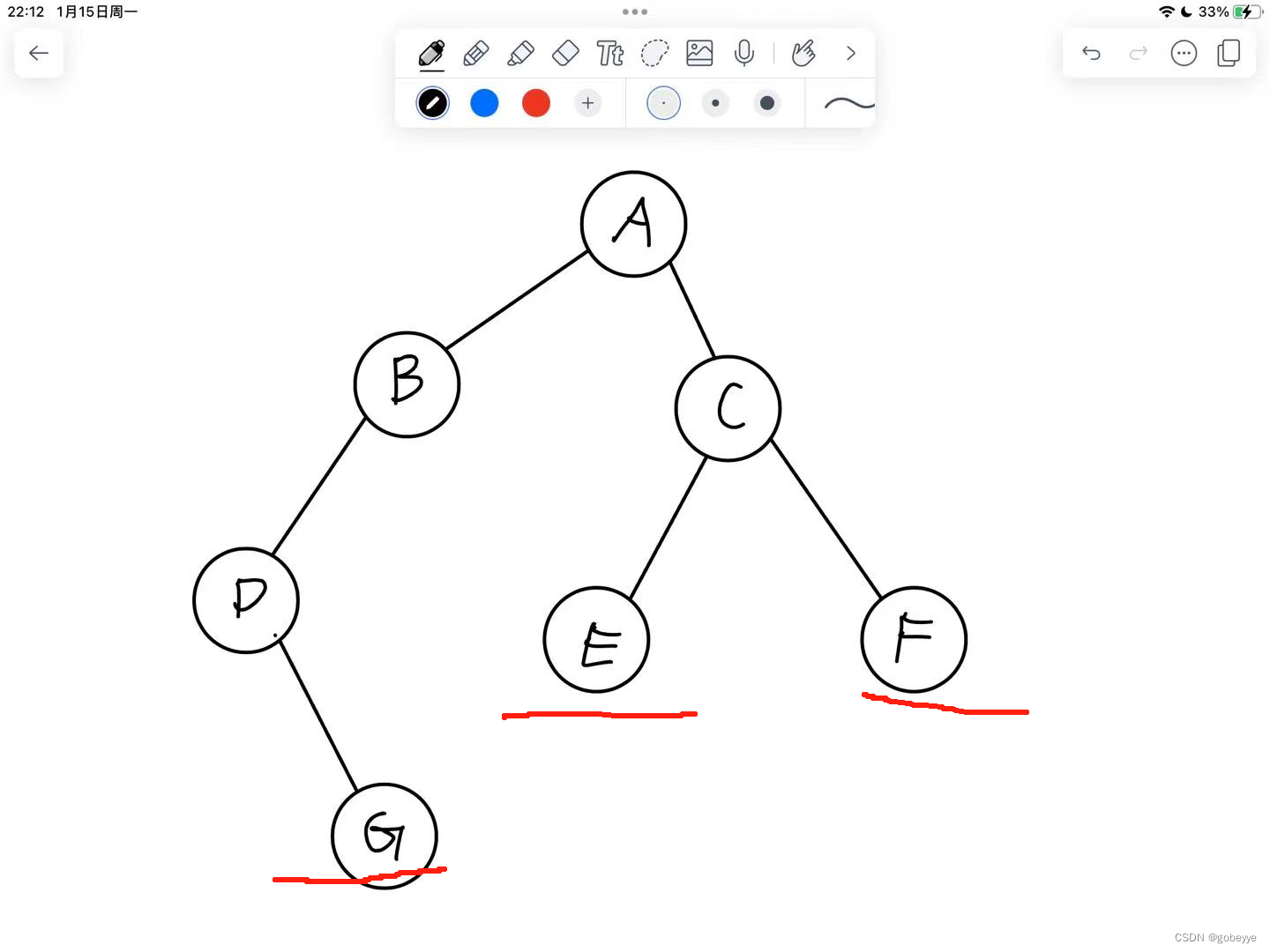
对应的函数如下DispLeaf（BTNode*b）

通过判断有无孩子结点来判断他是不是叶子结点（最下面那个结点）,如果不是就递归左右子树找叶子。此题三种遍历都能实现，下面代码是先序遍历，如果把if和DispLeaf(b->lchild);交换就变成中序遍历，同理如果把DispLeaf(b->lchild)和?DispLeaf(b->rchild);同时先上移，这样就变成后序遍历。

void DispLeaf(BTNode* b)//求叶子结点
{
	if (b != NULL)
	{
		if (b->lchild == NULL && b->rchild == NULL)
		{
			printf("%c ", b->data);
		}
		DispLeaf(b->lchild);
		DispLeaf(b->rchild);
	}

}

运行结果如下：

例题2：

设计一个算法求二叉树b中第k层的结点个数。

思路如下：函数名为void Lnodenum(BTNode* b, int h, int k, int* n),其中h表示b所指的结点层次，n是引用型参数，由于求第k层的结点个数，在初始调用时，b为根结点指针，h为1，n赋值为0，即调用方式时n=0；Lnodenum(b, 1, k, &t);

采用先序遍历的函数如下，如果想用中序和后序的话按照例题一的修改方法即可。

void Lnodenum(BTNode* b, int h, int k, int* n)
{
	if (b == NULL)
	{
		return;
	}
	else if (h == k)
	{
		if(b->data!=' ') *n = *n + 1;		
		return;
	}
	else if (h < k)
	{
		Lnodenum(b->lchild, h + 1, k, n);//特别注意不要&n
		Lnodenum(b->rchild, h + 1, k, n);
	}
}

运行结果如下：

对照上面给出的二叉树的图大家可以试试。

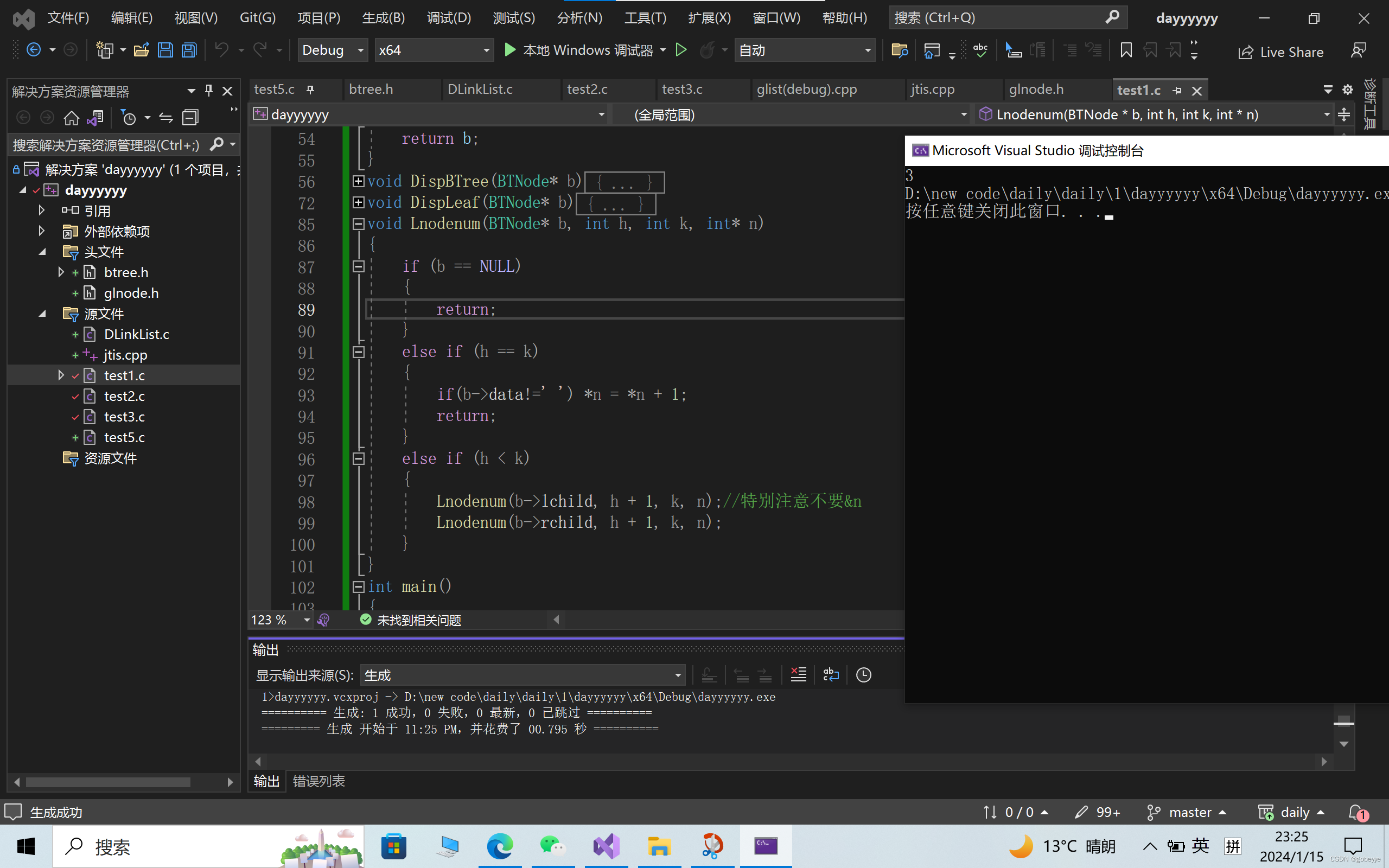
对应的main函数。

直接将上面的两个函数加进去即可，其中CreateBTree和DispBTree在我的上一篇文章二叉树的基本运算中已经讲的很清楚了，如果有朋友们不是很清楚的话，可以去上一篇文章看看，写的很详细哦。

#define  _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
typedef char ElemType;
#define MaxSize 100
typedef struct node
{
	struct node* lchild, * rchild;
	ElemType data;
}BTNode;
BTNode* CreateBTree(char* str)
{
	BTNode* SqStack[MaxSize];
	BTNode* b;
	BTNode* p = NULL;
	b = NULL;
	int top = -1;
	char ch;
	int j = 0;
	ch = str[j];
	int k = 0;
	while (ch != '\0')
	{
		switch (ch)
		{
		case '(':k = 1; top++; SqStack[top] = p; break;
		case ')':top--; break;
		case ',':k = 2; break;
		default:
		{
			p = (BTNode*)malloc(sizeof(BTNode));
			p->data = ch;
			p->lchild = p->rchild = NULL;
			if (b == NULL)
			{
				b = p;
			}
			else
			{
				switch (k)
				{
				case 1:SqStack[top]->lchild = p; break;
				case 2:SqStack[top]->rchild = p; break;
				}
			}
		}
		}
		j++;
		ch = str[j];
	}
	return b;
}
void DispBTree(BTNode* b)
{
	if (b != NULL)
	{
		printf("%c", b->data);
		if (b->lchild != NULL || b->rchild != NULL)
		{
			printf("(");
			DispBTree(b->lchild);
			if (b->rchild != NULL) printf(",");
			DispBTree(b->rchild);
			printf(")");
		}
	}

}


int main()
{
	char str[] = "A(B(D( ,G)),C(E,F))";
	BTNode* b = CreateBTree(str);
	//DispLeaf(b);
	int t = 0;
	Lnodenum(b, 1, 3, &t);
	printf("%d", t);
	//DispBTree(b);
	return 0;
}

层次遍历例题：

设计一个算法将二叉树按层次遍历输出：

层次遍历过程是先将根结点进队，在队不空是循环：出队一个结点p并访问它，若它有左孩子，将左孩子进队：若它有右孩子，将有孩子进队。如此操作，直到队空为止。次过程称为基本层次遍历过程，对应的算法代码如下。本身代码不多主要是实现队列挺麻烦的（这就是为什么c语言没有别的语言效率那么高的原因，别的语言有的自带队列）。

#include <stdio.h>
#include <stdbool.h>
#include <stdlib.h>
typedef char ElemType;
#define MaxSize 100
typedef struct node
{
	struct node* lchild;
	struct node* rchild;
	ElemType data;
}BTNode;
typedef struct 
{
	BTNode* data[MaxSize];
	int front, rear;
}SqQueue;
//基本层次遍历算法
SqQueue* InitQueue()
{
	SqQueue* obj = (SqQueue*)malloc(sizeof(SqQueue));
	obj->front = obj->rear = -1;
	return obj;
}
bool enQueue(SqQueue* qu, BTNode* b)
{
	qu->rear++;
	qu->data[qu->rear] = b;
	return true;
}
bool EmptyQueue(SqQueue* qu)
{
	return (qu->front == qu->rear);
}
bool deQueue(SqQueue* qu, BTNode** b)
{
	qu->front++;
	*b = qu->data[qu->front];
	return true;
}
void DestroyQueue(SqQueue* qu)
{
	free(qu);
}
void LevelOrder(BTNode* b)
{
	BTNode* p = NULL;
	SqQueue* qu;
	qu = InitQueue();
	enQueue(qu, b);
	while (!EmptyQueue(qu))
	{
		deQueue(qu, &p);
		printf("%c ", p->data);
		if (p->lchild != NULL)
			enQueue(qu, p->lchild);
		if (p->rchild != NULL)
			enQueue(qu, p->rchild);
	}
	DestroyQueue(qu);
}
BTNode* CreateBTree(char str[])
{
	BTNode* b = (BTNode*)malloc(sizeof(BTNode));
	BTNode* St[MaxSize];
	b = NULL;
	BTNode* p = NULL;
	int top = -1;
	char ch;
	int j = 0;
	ch = str[j];
	int k;
	while (ch != '\0')
	{
		switch (ch)
		{
		case '(':top++; St[top] = p; k = 1; break;
		case ')':top--; break;
		case ',':k = 2; break;
		default:
		{
			p = (BTNode*)malloc(sizeof(BTNode));
			p->data = ch;
			p->lchild = p->rchild = NULL;
			if (b == NULL)
			{
				b = p;
			}
			else
			{
				switch (k)
				{
				case 1:St[top]->lchild = p; break;
				case 2:St[top]->rchild = p; break;
				}
			}
		}
		}
		j++;
		ch = str[j];
	}
	return b;
}
int main()
{
	char str[] = "A(B(D( ,G)),C(E,F))";
	BTNode* b = CreateBTree(str);
	LevelOrder(b);
}

以上便是先序中序后序层次遍历的算法及例题。文章到这也就到了尾声啦，感谢观看🎉🎉🎉

结语：

其实写博客不仅仅是为了教大家，同时这也有利于我巩固自己的知识点，和一个学习的总结，由于作者水平有限，对文章有任何问题的还请指出，接受大家的批评，让我改进，如果大家有所收获的话还请不要吝啬你们的点赞收藏和关注，这可以激励我写出更加优秀的文章。