专题四：前缀和

一.一维前缀和(模板)：

一维前缀和

1.思路一：暴力解法

1.输入数组长度n和查询次数q。
2.使用一个一维数组保存数据。
3.使用一个循环获取q次需要查询范围的数据。
4.遍历r-l+1次进行一个范围求和然后输出。
5.时间复杂度：O(n^2)
6.通过不了所有的测试用例。

2.思路二：前缀和思路

1.输入数组长度n和查询次数q。
2.使用一个一维数组保存数据。
3.构建一个前缀和的一个数组。

4.使用一个循环获取q次需要查询范围的数据。
5.时间复杂度：O(n^2)
6.通过不了所有的测试用例。

#include <iostream>
#include <vector>
using namespace std;

int main()
{
    //1.输入数组长度和查询次数： 
    int n =0,q=0;
    cin>>n>>q;
    //2.输入数组数据：
    vector<int> arr(n+1);
    for(int i=1;i<=n;i++) cin>>arr[i];
    //3.前缀和数组：
    vector<long long> bp(n+1);
    for(int i=1;i<=n;i++) bp[i] = bp[i-1] + arr[i];
    //4.计算和：
    int i=0,r=0;
    while(q!=0)
    {
        cin>>i>>r;
        cout<<(bp[r] - bp[i-1])<<endl;
        q--;
    }
}

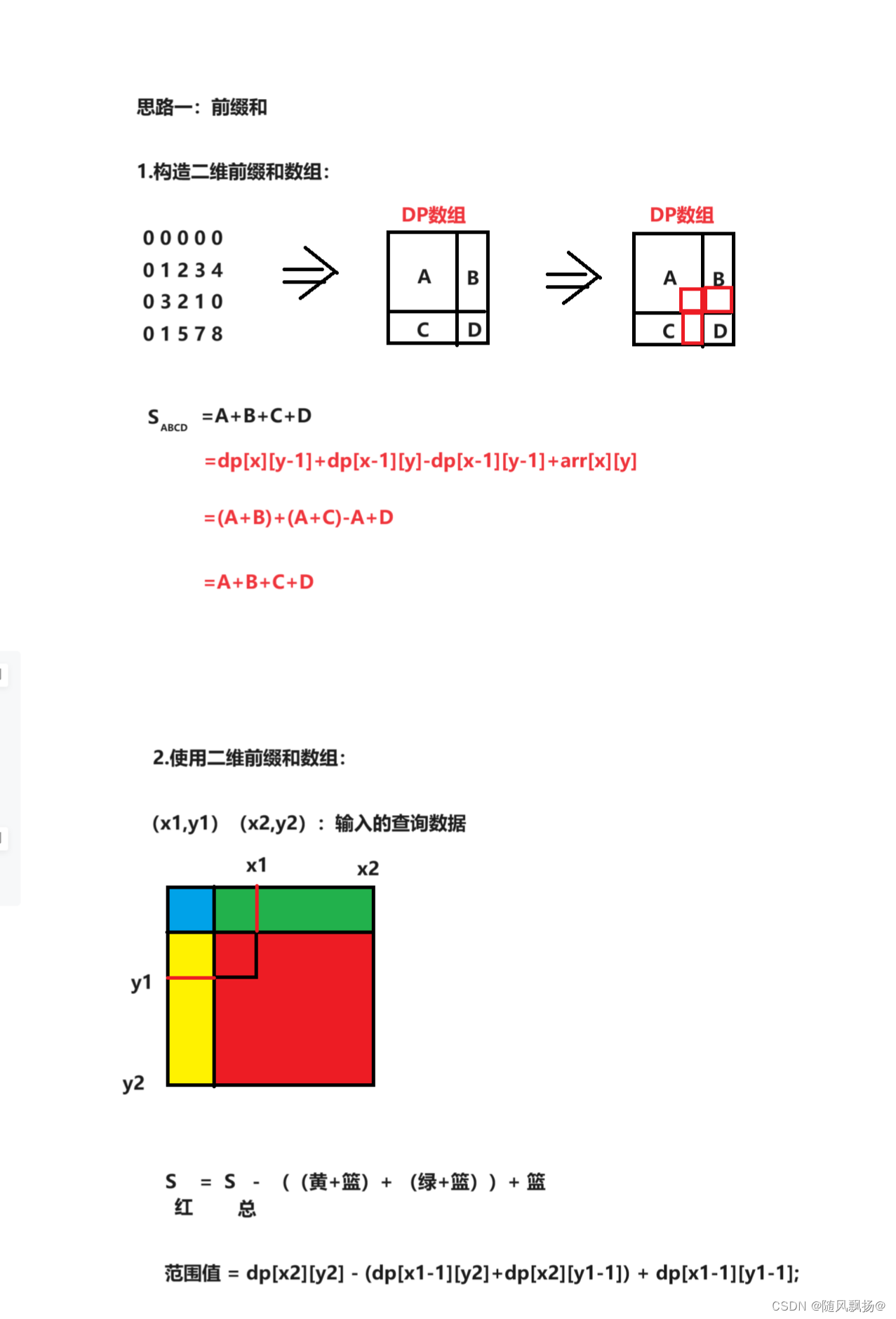
二. 二维前缀和(模板)：

二维前缀和

1.思路一：构造前缀和数组

#include <iostream>
#include <vector>
using namespace std;

int main()
{
    //1.n行m列的一个二维数组：
    int n = 0, m = 0, q = 0;
    cin >> n >> m >> q;
    //2.数组输入数据：
    vector<vector<int>> vv((n + 1),vector<int>(m+1));
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)cin >> vv[i][j];
    }

    //3.创造二维的求和dp数组
    vector<vector<long long>> dp((n + 1), vector<long long>(m + 1));
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            dp[i][j] = ((dp[i][j - 1] + dp[i - 1][j]) - dp[i-1][j-1]) + vv[i][j];
        }
    }
    //4.数据查询：

    while (q != 0)
    {
        int x1 = 0, y1 = 0, x2 = 0, y2 = 0;
        cin >> x1 >> y1 >> x2 >> y2;

        cout << (dp[x2][y2] - (dp[x1 - 1][y2] + dp[x2][y1-1]) + dp[x1-1][y1-1]) << endl;
        q--;
    }


}

三.寻找数组的中心下标：

寻找数组的中心下标

1.思路一：前缀和

class Solution {
public:
    int pivotIndex(vector<int>& nums) {
        
        //1.构建前缀和数组：
        int n = nums.size();
        vector<int> dp(n+1);
        //2.前缀和数组值遍历：
        for(int i = 1 ; i<=n;i++) dp[i] = dp[i-1] + nums[i-1];

        //3.进行中心下标的寻找：
        int mid = -1;
        for(int i=1 ; i <= n ; i++)
        {
            if((dp[i-1] - dp[0]) == (dp[n] - dp[i]))
            {
                mid = i-1;
                break;
            }
        }
        //4.没有中心下标的情况：
        return (mid == -1? -1:mid);
    }
};

四.除自身以外数组的乘积：

除自身以外数组的乘积

1.思路一：暴力解法

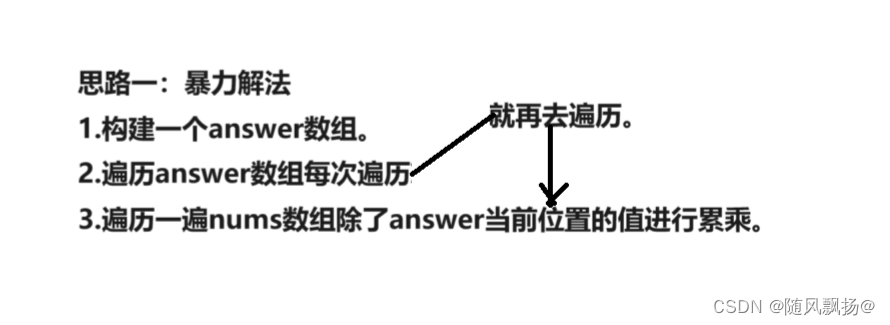
2.思路二：前缀积+后缀积

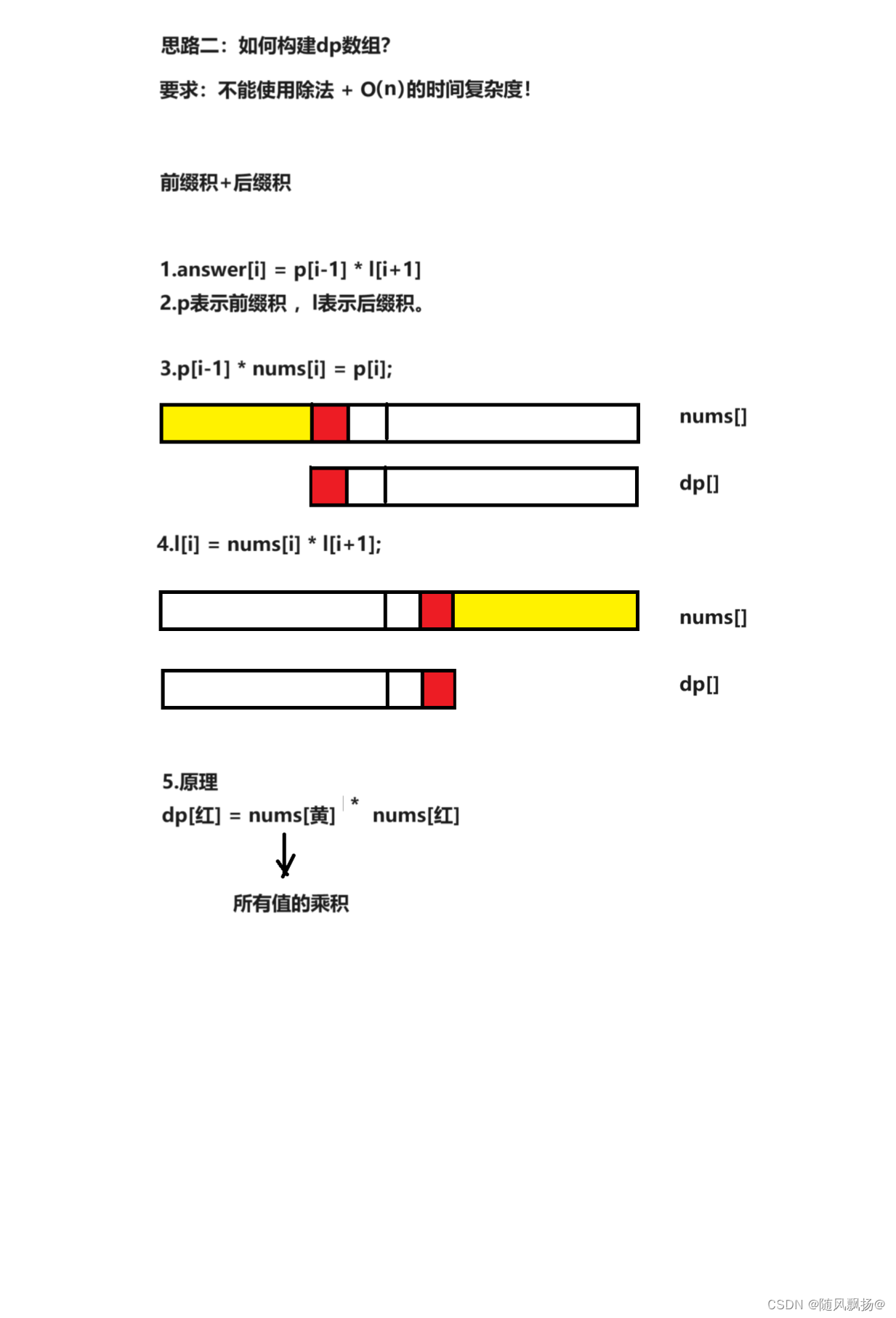
class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {

        //1.前缀积+后缀积
        int n = nums.size();
        vector<int> left(n + 1, 1);
        vector<int> right(n + 1, 1);

        //2.遍历确定前缀积+后缀积的值：
        for (int i = 1; i <= n; i++) left[i] = left[i - 1] * nums[i - 1];
        for (int i = n - 1; i >= 0; i--) right[i] = right[i + 1] * nums[i];

        // 1  1  2  6  24
        // 24 24 12 4  1
        // 0  1  2  3  4

        //0   1   2  3
        //24  12  8  6
        vector<int> ret(n);
        //3.遍历ret数组并且赋值
        for (int i = 0; i < n; i++)
        {
            ret[i] = left[i] * right[i+1];
        }

        return ret;
    }
};

五.和为K的子数组：

和为K的子数组

1.思路一：前缀和+哈希

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        unordered_map<int,int> hash;
        hash[0]=1;
        int sum = 0 , ret = 0;
        for(auto n : nums)
        {
            sum+=n;
            if(hash.count(sum-k)) ret+=hash[sum-k];
            hash[sum]++;
        }
        return ret;
    }
};

六.前缀和可以被K整除的子数组：

前缀和可以被K整除的子数组

1.思路一：前缀和+哈希

class Solution {
public:
    int subarraysDivByK(vector<int>& nums, int k) {
        unordered_map<int,int> hash;
        hash[0] = 1;

        //1.开始遍历+判断
        int sum = 0 , ret = 0;
        for(auto a : nums)
        {
            sum+=a;
            int n = (sum%k + k) % k;

            if(hash.count(n)) ret+=hash[n];
            hash[n]++;
        }
        return ret;
    }
};

七.连续数组：

连续数组

1.思路一：

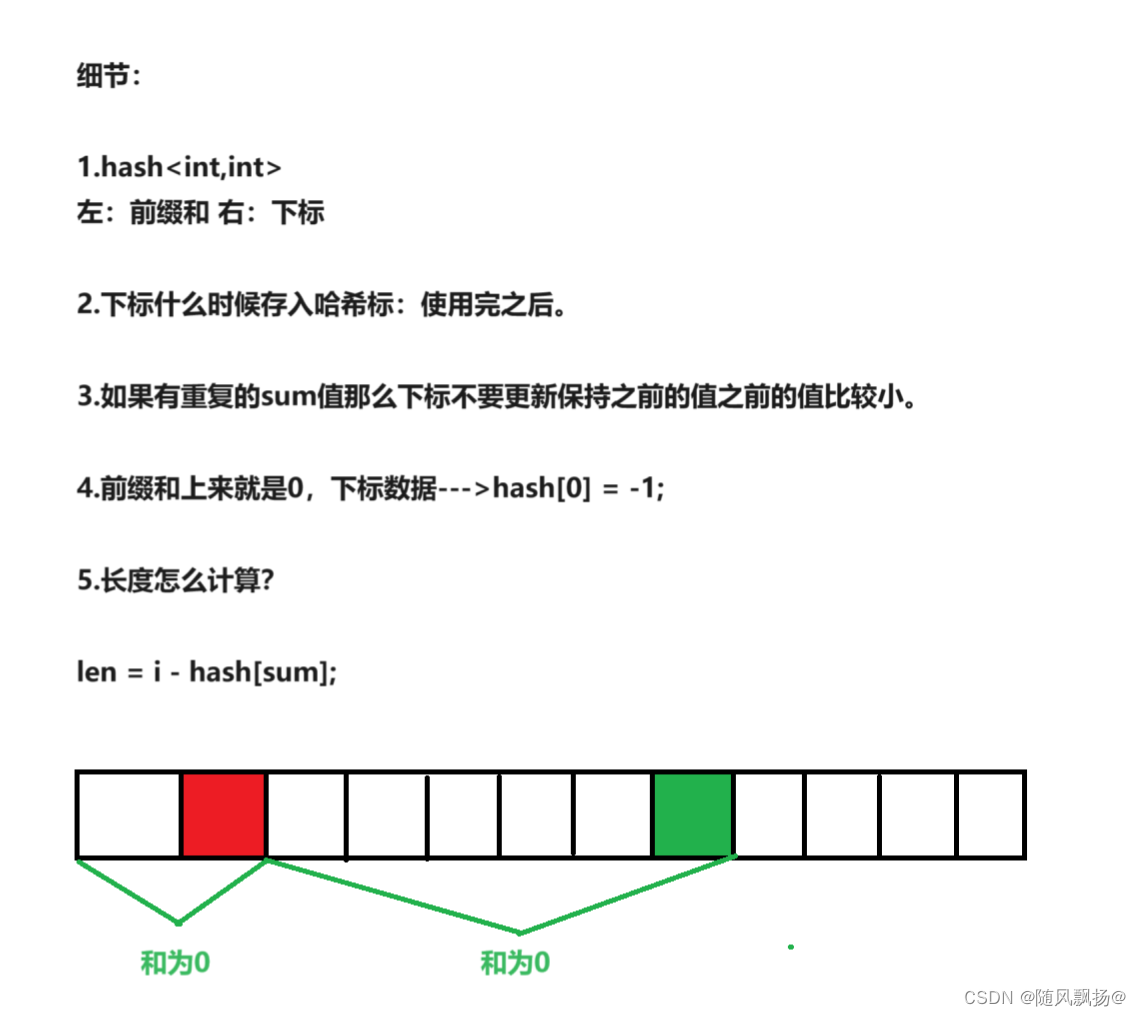
class Solution {
public:
    int findMaxLength(vector<int>& nums) {
        vector<int> nums_1(nums);
        for(auto& n:nums_1)
        {
            if(n==0) n = -1;
        }

        //2.hash+前缀和的思路
        unordered_map<int,int> hash;
        //1.前缀和为0的下标处理：
        hash[0] = -1;
        int sum = 0,ret = 0;
        for(int i=0;i<nums.size();i++)
        {
            sum+=nums_1[i];
            if(hash.count(sum)) ret = max(ret , i - hash[sum]);
            else hash[sum] = i;
        }
        return ret;
    }
};

八.矩阵区域和：

矩阵区域和

1.思路一：二维前缀和模板+细节处理

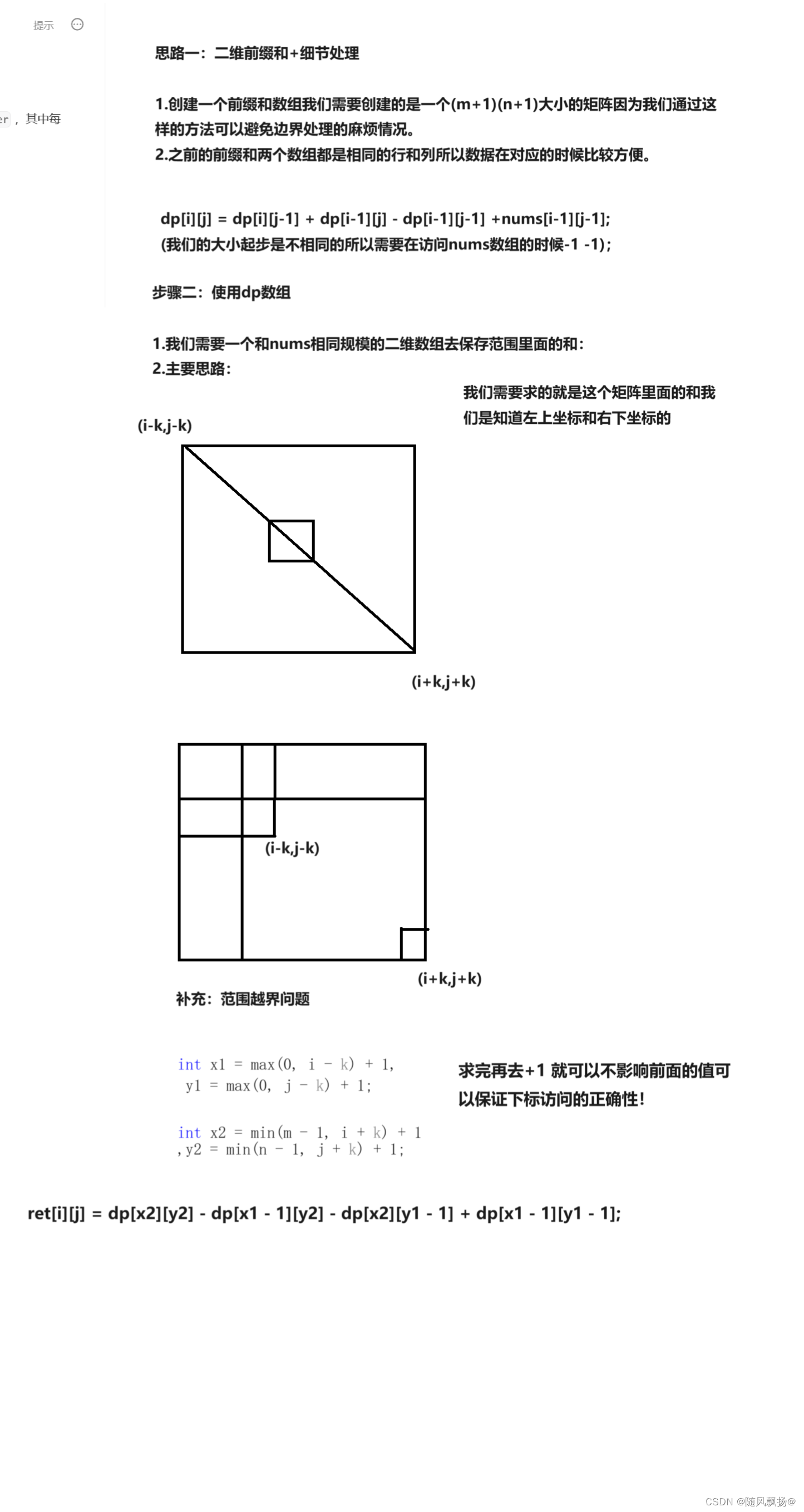
class Solution {
public:
    vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {
        int m = mat.size();
        int n = mat[0].size();

        //1.创建(m+1) * (n+1) 大小的二维数组
        vector<vector<int>> dp(m+1 , vector<int>(n+1));

        //2.dp数组赋值：
        for(int i=1 ; i<=m ; i++)
        {
            for(int j=1 ; j<=n ; j++)
            {
                dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + mat[i-1][j-1];
            }
        }

        //3.使用dp数组并且考虑i-k 和 j-k的越界问题：
        vector<vector<int>> ret(m,vector<int>(n));

        for(int i=0 ; i<m ; i++)
        {
            for(int j=0 ; j<n ; j++)
            {
                int x1 = max(0, i - k) + 1, y1 = max(0, j - k) + 1;
                int x2 = min(m - 1, i + k) + 1, y2 = min(n - 1, j + k) + 1;
                
                ret[i][j] = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] +
                    dp[x1 - 1][y1 - 1];
            }
        }
        return ret;
     }
};