多目标优化中常用的多目标遗传算法NSGA2【3】
#Attention Please
#网上看了很多关于NSGA2的讲解,但是总觉得少了点意思,为此经过多出选择裁剪给出了最通俗易懂的讲解,如果错误欢迎批评指正。
#以下部分内容来源于网上公开的讲解。
1、原理
了解NSGA2的前提是学会NSGA,而对于NSGA算法,我们需要了解非支配排序和遗传算法,进一步地就过渡到NSGA2;
NSGA2也就是用到了所谓的快速非支配排序算法,以及采用精英策略对新产生的父代和子代解进行选择;
这里精英策略作为一个主循环,在主循环里嵌套选择策略,对新生成的解进行快速非支配排序。
2、过程
随机初始化产生一组解--->非支配排序进行选择--->交叉--->变异--->将旧解【父代解】和新解【子代解】合并--->对合并后的解进行精英策略选择生成父代--->循环以上过程直到达到终止条件。
3、关键步骤
适应度:可以通俗理解就是你定义的所谓目标函数,当然几个目标【多目标】就可以算出几个适应度的数值。
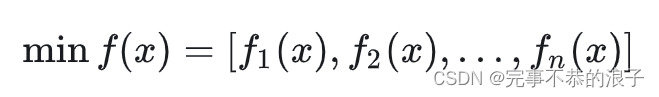
如上式中的可以作为其中一个适应度函数。
更形象的,我们可以建立一个二维坐标系,这里的两个维度代表的是2个目标的适应度函数。
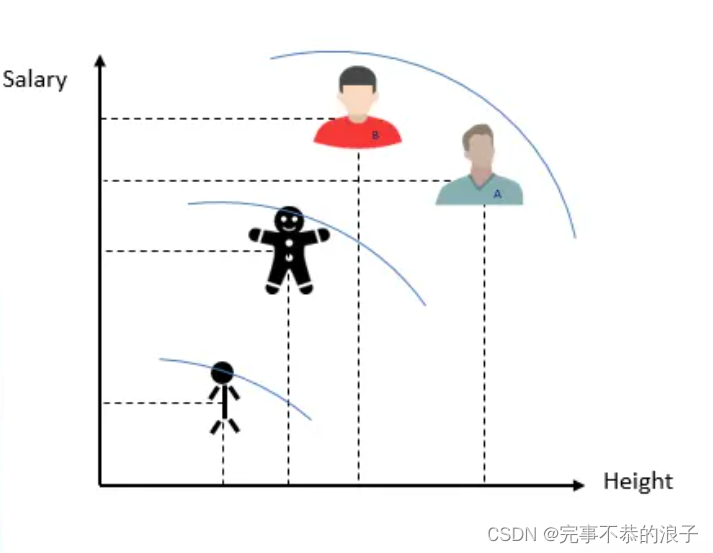
非支配排序:以上图为例,我们可以看到4个小人分别位于不同的层,并且在两个坐标轴都有对应的数值:Salary和Height,现在要做的就是:A、B、C、D这四个人的综合评价指标,谁的更好呢?我们到底是更多的考虑身高还是更多的考虑薪资水平呢?由此,我们引出非支配排序的概念。
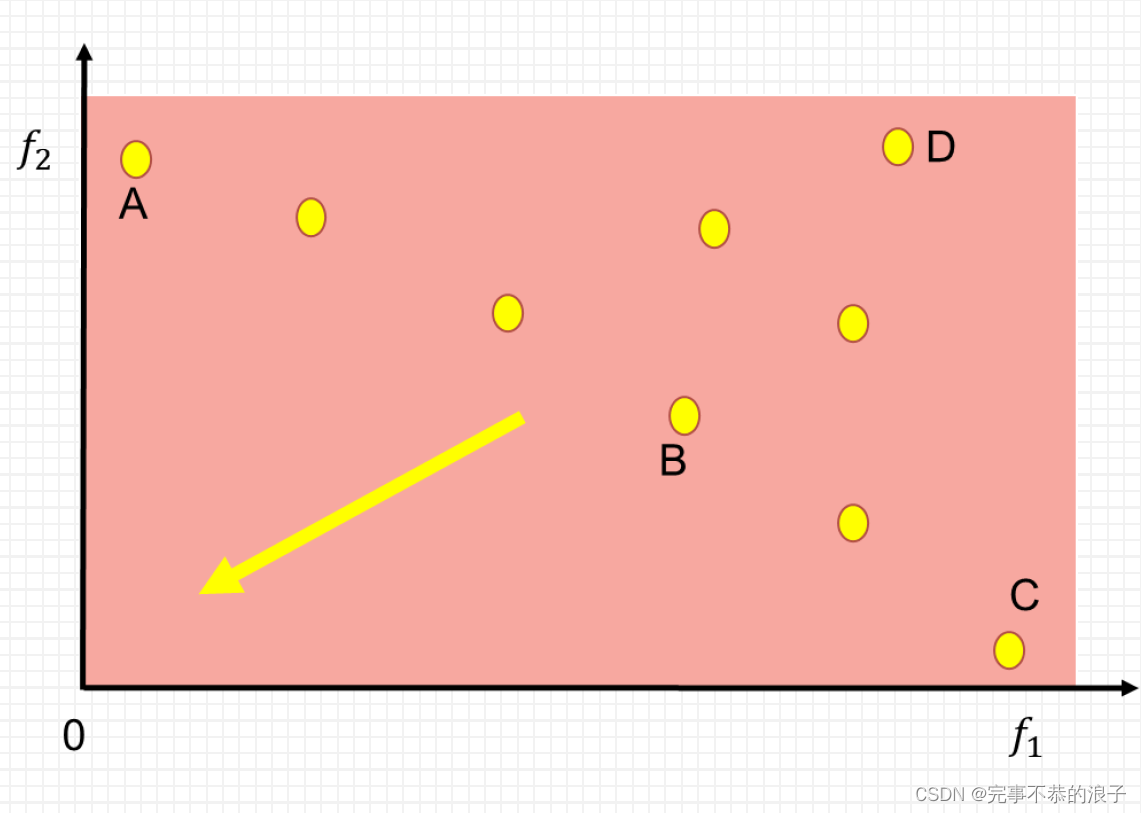


拥挤距离:以下定义来源于原论文,《A Fast and Elitist Multiobjective Genetic Algorithm:NSGA-II》

中文版本的解释如下:


为了获得对种群中某一特定解附近的密度估计, 我们沿着对应目标计算这个解两侧的两点间的平均距离。 这个值是对用最近的邻居作为顶点形成的长方体的周长的估计称之为拥挤距离)。在图 1 中, 第i 个解在其前沿的拥挤距离(用实心圆标记)是长方体的平均边长(用虚线框表示。(用实心圆标记的点是同一非支配前沿的解)

非支配排序:

快速非支配排序:NSGA2


精英策略:

首先有一群具有多个目标的个体做为父代,在每个迭代中,在GA操作之后合并父代和子代。通过非支配排序,我们将所有个体分类到不同的帕累托最优前沿层次。然后按照不同层次的顺序从帕累托最优前沿选择个体作为下一个种群。对于多样性保护,还计算了“拥挤距离”。拥挤距离比较将算法各阶段的选择过程引向一致展开的帕累托最优前沿。


4、引用
[8]A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II
5、附赠一张很精辟的图

如果你觉得不错,佛系随缘打赏,感谢,你的支持是我继续耕耘的动力。


本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 俄罗斯联邦税务局遭乌克兰入侵,数据库和副本被清空,政府数据安全不容忽视
- 基于BGP/MPLS VPN跨域互联方案B校园网的研究与仿真
- HTML5+CSS3小实例:文字溶合切换效果
- 给我狠狠的入Redis
- 2023-12-18 最大二叉树、合并二叉树、二叉搜索树中的搜索、验证二叉搜索树
- 【使用Ubuntu编译FFmpeg生成Android动态库/静态库】
- Git提交代码发生冲突的场景与解决方案
- MySQL修炼手册2:MySQL基础查询语句解析
- 【DB2】Maxlocks和防止锁升级
- SV与C语言在验证环境中的交互