【算法与数据结构】509、LeetCode斐波那契数

所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。

一、题目

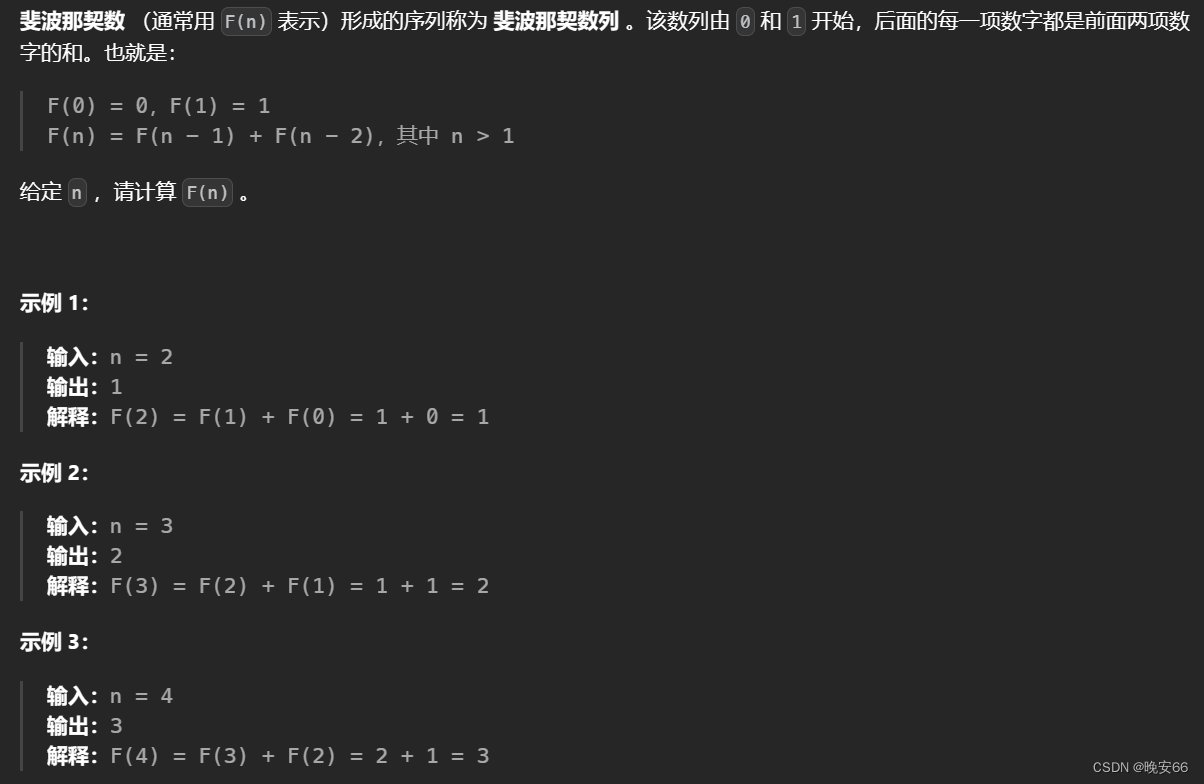
二、递归，动态规划解法

2.1 递归解法

??思路分析：斐波那契数列可以用递归实现，下面直接给出代码，非常简单。递归的代码简单，但是递归的速度很慢，因为递归代码中的时间复杂度为$O(n^2)$。
??程序如下：

class Solution {
public:
	int fib(int n) {		// 1 1 2 3 5 8 13 21
		if (n <= 1) return n;
		return fib(n - 1) + fib(n - 2);
	}
};

复杂度分析：

• 时间复杂度： $O(n^2)$，一个fib(n)时间复杂度为$O((1+n)?n/2)=O(n^2)$。
• 空间复杂度：$O(n)$，递归中栈所需的空间。

2.2 动态规划解法

??思路分析：动态数组为$dp[i]=dp[i?1]+dp[i?2]$，根据此公式，写出如下代码。
??程序如下：

class Solution {
public:
	int fib(int n) {		// 1 1 2 3 5 8 13 21
		if (n <= 1) return n;
		vector<int> dp(n + 1);	// 动态规划中的dp数组
		dp[0] = 0;
		dp[1] = 1;
		for (int i = 2; i <= n; i++) {
			dp[i] = dp[i - 1] + dp[i - 2];
		}
		return dp[n];
	}
};

复杂度分析：

• 时间复杂度： $O(n)$。
• 空间复杂度：$O(n)$。

??但是实际上，我们可以看到计算斐波那契数列只需要用到两个值，不必保留整个动态数组。因此对上述代码进行内存优化，空间复杂度从$O(n)$变成$O(1)$。

class Solution {
public:
	int fib(int n) {		// 1 1 2 3 5 8 13 21
		if (n <= 1) return n;
		int dp[2];
		dp[0] = 0;
		dp[1] = 1;
		for (int i = 2; i <= n; i++) {
			int sum = dp[0] + dp[1];
			dp[0] = dp[1];
			dp[1] = sum;
		}
		return dp[1];
	}
};

复杂度分析：

• 时间复杂度： $O(n)$。
• 空间复杂度：$O(1)$。

三、完整代码

# include <iostream>
# include <vector>
using namespace std;

//class Solution {
//public:
//	int fib(int n) {		// 1 1 2 3 5 8 13 21
//		if (n <= 1) return n;
//		return fib(n - 1) + fib(n - 2);
//	}
//};

//class Solution {
//public:
//	int fib(int n) {		// 1 1 2 3 5 8 13 21
//		if (n <= 1) return n;
//		vector<int> dp(n + 1);	// 动态规划中的dp数组
//		dp[0] = 0;
//		dp[1] = 1;
//		for (int i = 2; i <= n; i++) {
//			dp[i] = dp[i - 1] + dp[i - 2];
//		}
//		return dp[n];
//	}
//};

class Solution {
public:
	int fib(int n) {		// 1 1 2 3 5 8 13 21
		if (n <= 1) return n;
		int dp[2];
		dp[0] = 0;
		dp[1] = 1;
		for (int i = 2; i <= n; i++) {
			int sum = dp[0] + dp[1];
			dp[0] = dp[1];
			dp[1] = sum;
		}
		return dp[1];
	}
};

int main() {
	int n = 4;
	Solution s1;
	int result = s1.fib(n);
	cout << result << endl;
	system("pause");
	return 0;
}

end