R语言数据探索和分析4-波士顿数据集分析

数据集介绍

卡内基梅隆大学收集，StatLib库，1978年，涵盖了麻省波士顿的506个不同郊区的房屋数据。一共含有506条数据。每条数据14个字段，包含13个属性，和一个房价的平均值。

1.数据加载和初步探索

读取数据

# 查看前几行数据
head(Boston)

可视化房间数和房价的关系

  # 可视化房间数和房价的关系
ggplot(Boston, aes(x = rm, y = medv)) +
  geom_point(aes(color = medv)) +
  labs(title = "Room Number vs. Median Value",
       x = "Average number of rooms per dwelling",
       y = "Median value of owner-occupied homes in $1000's") +
  theme_minimal()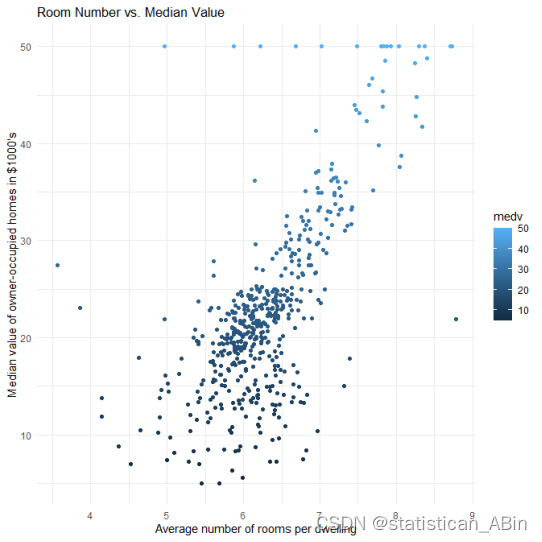

房间数量（横轴）和房屋中位价值（纵轴）之间似乎存在正相关，即房间数量越多，房屋的中位价值通常也越高。大部分数据点集中在5到7个房间之间，对应的中位价值在10,000到30,000美元之间。随着房间数量的增加，房屋中位价值的分布范围也在增加，尤其是在房间数量超过6个之后。数据点的颜色深度表示房屋中位价值的大小，颜色越深表示价值越高。可以看出，价值超过40,000美元的房屋数量较少。

可视化房价的分布

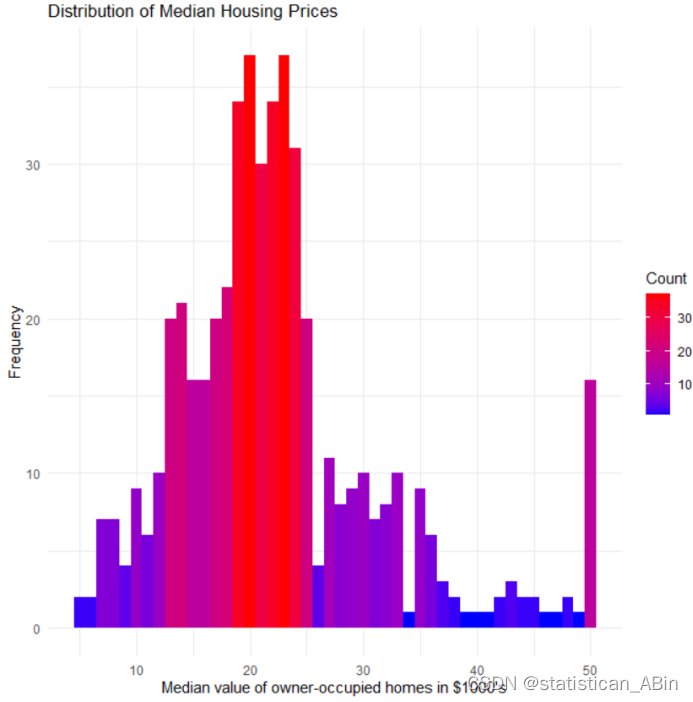颜色的变化代表频率的变化，从紫色（低频率）到红色（高频率），我们可以看到大部分房屋的中位价值集中在紫色至红色区间，即中位价值15,000至25,000美元之间。高价值区域（例如大于35,000美元的房屋）的频率较低，这些可能代表特定的高端住宅区。房价分布的尾部较长，显示了一些非常高价值的房屋，这些可能是豪宅或位于特别受欢迎的地区。

????????2.多元线性回归

创建线性回归模型，medv为因变量，其他所有变量为自变量，结果如下图：

# 创建线性回归模型，medv为因变量，其他所有变量为自变量
linear_model <- lm(medv ~ ., data=Boston)
# 输出模型摘要来查看结果
summary(linear_model)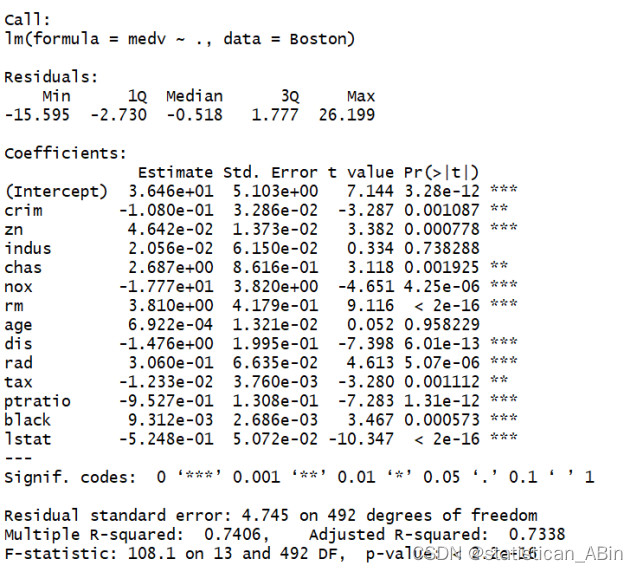

在这个模型输出中，变量rm（房间数）的系数是正的且高度显著（p值 < 2e-16），这表明房间数的增加与medv（可能代表房屋中位数价值）正相关。其他变量的正负系数则表示它们与目标变量的关系方向，系数的大小和显著性水平表示其影响的大小和信度。

3.主成分分析

PCA前的数据标准化，再带入模型：

从PCA结果摘要中，我们可以观察到：

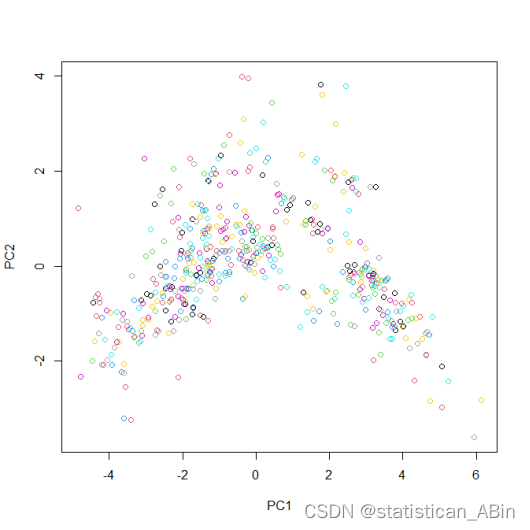
标准偏差（Standard Deviation）：每个主成分的标准偏差越大，表示该成分解释的方差越多。第一个主成分（PC1）有最大的标准偏差，因此它解释了数据中最大部分的方差。方差比例（Proportion of Variance）：PC1单独解释了约47.13%的方差，而前两个主成分（PC1和PC2）加起来解释了大约58.16%的方差。累计方差比例（Cumulative Proportion）：前三个主成分累计可以解释约67.71%的方差，而要解释超过90%的方差需要至少前十个主成分。

散点图中每个点代表数据集中的一个观察（房屋），点的位置由该房屋在PC1和PC2上的得分决定。点的颜色代表房屋的属性。我们可以看到数据在PC1和PC2形成的新空间中分布的模式，但没有明显的聚类或分离势。