二叉树与堆的深度解析:数据结构中的关键概念及应用


.
专栏:数据结构|Linux|C语言
路漫漫其修远兮,吾将上下而求索
文章目录
前言
在计算机科学的丰富和多样的领域中,数据结构扮演着核心角色。特别是树和堆,作为高效组织和处理数据的关键结构,它们在算法设计和系统实现中占据着重要位置。从文件系统的层次组织到优先队列的管理,理解这些结构的基础原理对于深入掌握计算机科学至关重要。本文旨在深入探讨树和堆的基本概念、性质及其在实际中的应用,为初学者和有志者提供一个明确的理解路径。
树概念
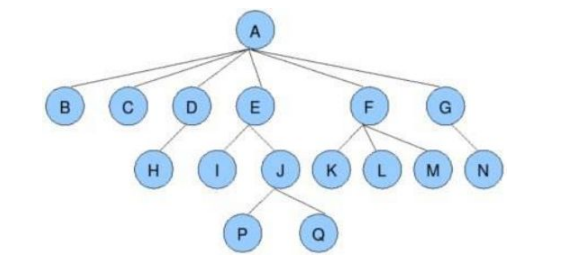
树是一种非线性数据结构,由n(n≥0)个节点构成,这些节点形成了一个具有明确层次的集合。这种结构被称为‘树’,因为它类似于一棵倒置的真实树,即其根部位于顶部,而叶节点则位于底部。
在这种结构中,有一个特殊的节点称为根节点,它是唯一一个没有前驱(即父节点)的节点。
除了根节点,其他所有节点被划分为M(M>0)个互不相交的子集T1、T2、……、Tm。每个子集Ti(1≤i≤m)本身又构成一棵结构上与原树相似的子树。”每棵子树的根节点恰有一个前驱(父节点)且可能有多个后继(子节点)。这种自相似的性质是树的一个关键特征,体现了其递归定义。。
注意:
树形结构中,子树之间不能有交集,否则就不是树形结构
树的基本概念及术语
基本概念及术语
根节点:想象一棵倒立的树,最顶部的那个点是根节点。在数据结构的树中,所有结构都是从这个根节点展开的。
节点:树中的每一个点称为节点,类似于树的小枝,可以向外延伸形成更多分支。
叶节点:位于树底部的节点,没有子节点,就像树上的叶子。
子树:从树中任一节点向下的部分,可以看作是一棵独立的、较小的树。
节点的度:一个节点含有的子树数量。例如,如果节点A有6个子树,那么A的度是6。
非终端节点/分支节点:度不为0的节点,即含有子节点的节点。
双亲节点/父节点:含有子节点的节点,这个节点是其子节点的父节点。
孩子节点/子节点:一个节点的直接下级节点。
兄弟节点:拥有相同父节点的节点。
树的度:树中所有节点的度中的最大值。
节点的层次:从根节点开始,根节点是第1层,其子节点是第2层,依此类推。
树的高度/深度:树中节点的最大层次数。
堂兄弟节点:父节点处于同一层的节点。
节点的祖先:从根节点到该节点路径上的所有节点。
子孙:某节点的所有下级节点。
森林:由多棵互不相交的树组成的集合。
以家谱为例
家谱中的曾祖父是根节点。
他的孩子(例如父亲和父亲的兄弟姐妹)是中间节点。
孙子辈(例如你)是叶节点。
在这个例子中,每一代都可以视作一个单独的“子树”。
树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间
的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法
等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
孩子兄弟表示法简介
在孩子兄弟表示法中,每个节点存储两个指针:
孩子指针:指向该节点的第一个孩子。
兄弟指针:指向同一父节点的下一个兄弟。
typedef int DataType;
struct Node
{
struct Node* _firstChild1; // 第一个孩子结点
struct Node* _pNextBrother; // 指向其下一个兄弟结点
DataType _data; // 结点中的数据域
};
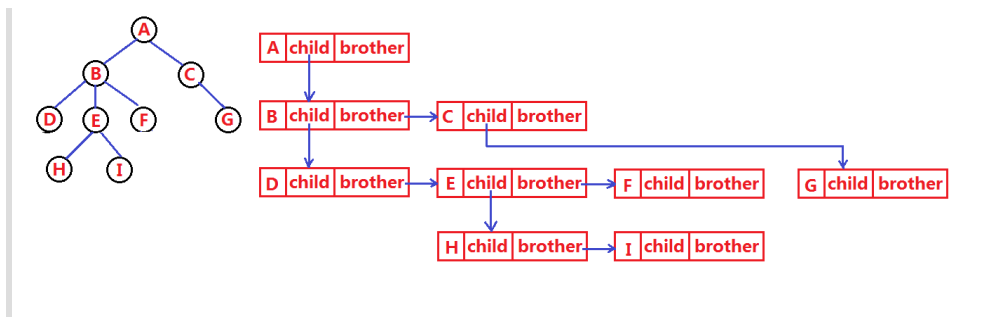
优势
使用孩子兄弟表示法的主要优点是它可以将任何复杂的树结构转换为类似二叉树的形式。这种转换使得对树的操作(如遍历、搜索等)更加统一和简化。此外,这种方法也便于处理树中节点数量变化的情况,如添加或删除子节点。
应用示例
假设我们有一个节点A,它有三个子节点B、C和D。在孩子兄弟表示法中,节点A的孩子指针指向B,B的兄弟指针指向C,C的兄弟指针指向D。这样,我们就可以通过节点A访问到它的所有子节点。
树在实际中的运用
文件系统的目录树结构
基本概念:在大多数操作系统中,文件和目录(文件夹)都是以树形结构组织的。这种结构允许用户方便地存储、访问和管理文件。
根目录:这个目录位于层级结构的顶部,相当于数据结构中的根节点。所有其他文件和目录都从这里开始分支。
目录和子目录:每个目录都可以包含文件或其他子目录(子节点)。这类似于树结构中的中间节点。
文件:位于树结构末端的文件类似于叶节点,它们不包含其他子目录或文件。
优点
组织性:树结构提供了一种清晰的方式来组织文件和目录,使得查找和访问文件变得直观和高效。
层级清晰:用户可以通过树的层级结构轻松地导航到特定文件或目录。
路径表示:文件的路径表示其在树结构中的位置,从根目录开始,通过各级子目录直到文件本身。
实例
想象您的电脑上有一个“文档”文件夹(目录)。在这个文件夹中,您可能有“工作”和“个人”这两个子文件夹。在“工作”文件夹中,您可能有不同的项目文件夹,每个项目文件夹中可能又有不同的文档和文件,依此类推。
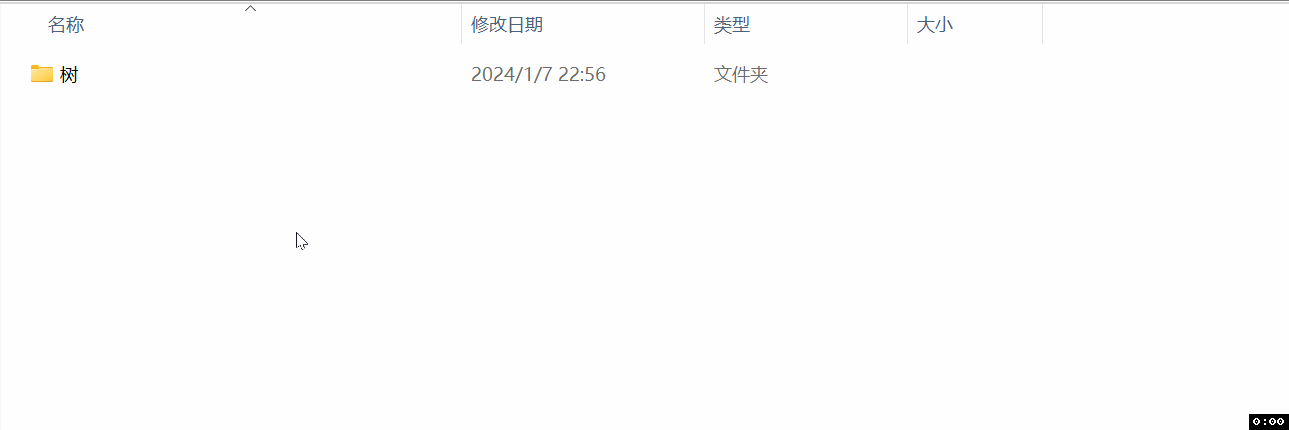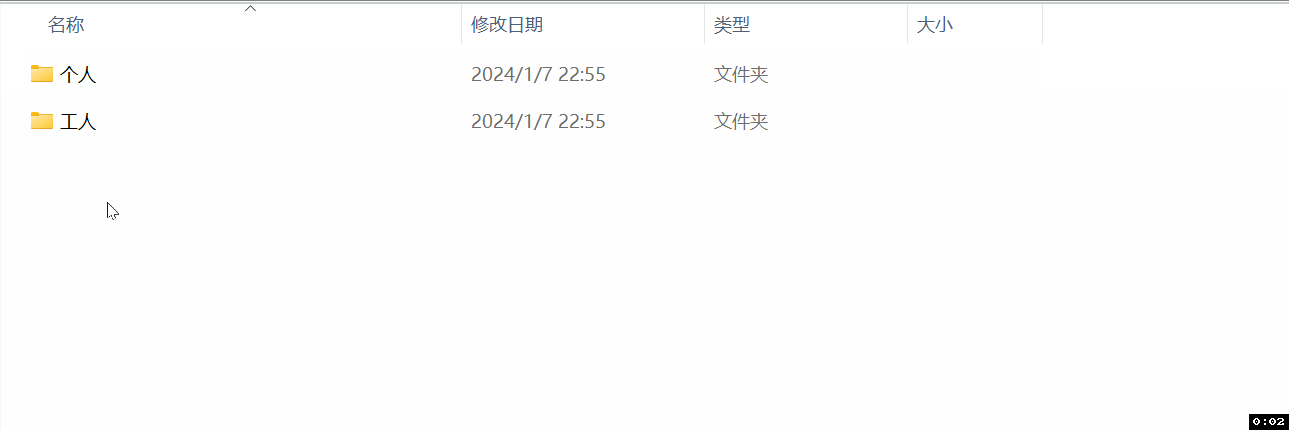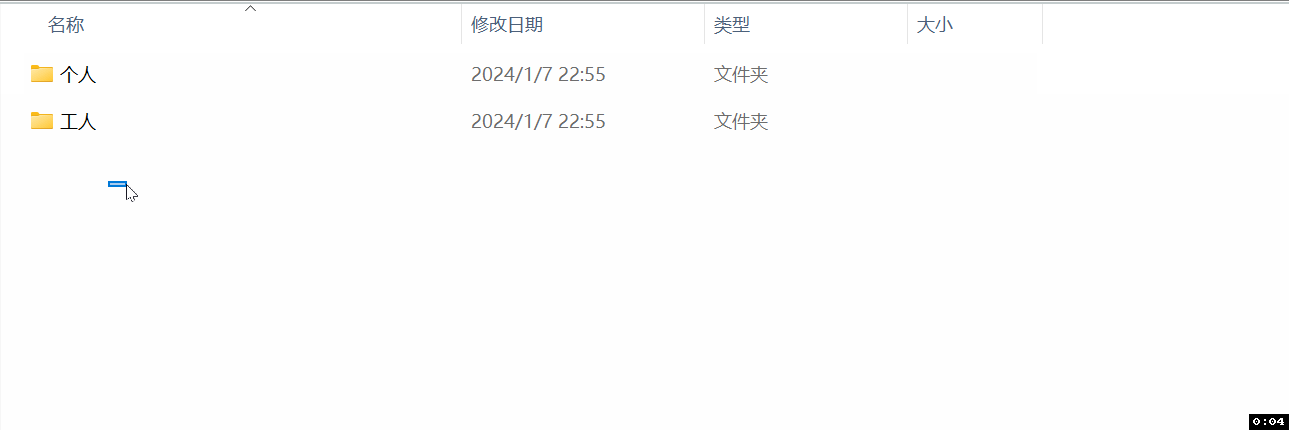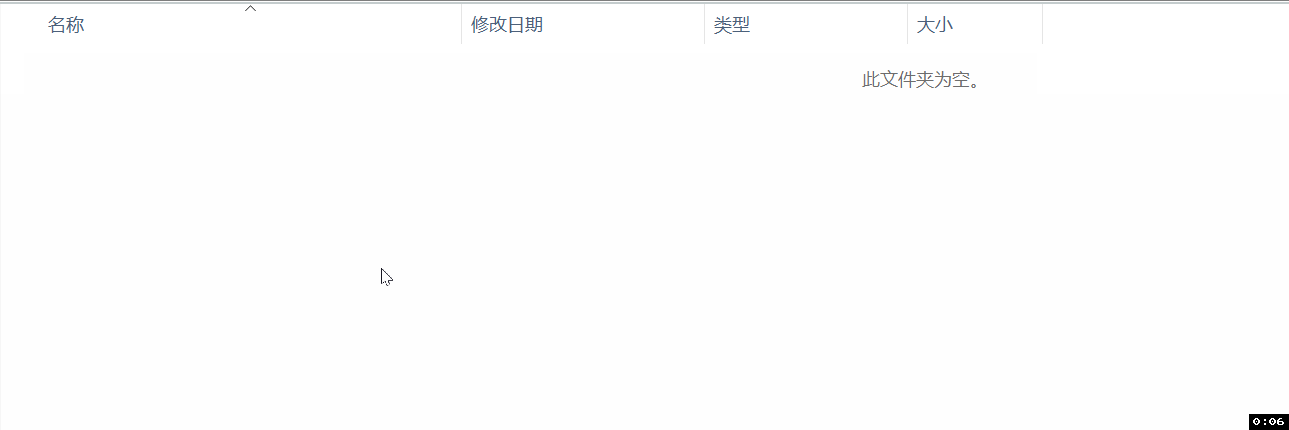
Windows中的树
在Windows操作系统中,文件系统的树结构通常通过资源管理器来可视化展示。这种表示方法有以下特点:
根节点:通常是驱动器,如C盘、D盘等。它们代表文件系统的起始点。
目录和子目录:每个驱动器下可以有多个目录(文件夹),并且每个目录可以进一步包含子目录。这些目录和子目录在树状结构中充当中间节点。
文件:位于树的末端,相当于叶节点。它们不包含进一步的子目录或文件。
Linux中的树
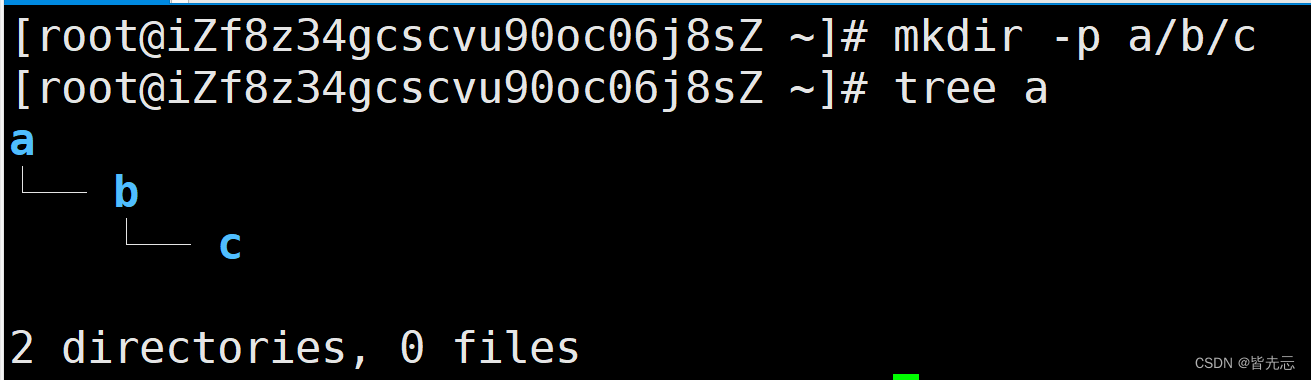
Linux操作系统中的文件系统结构与Windows类似,但有其特有的组织方式:
根目录:在Linux中,有一个全局的根目录“/”,它是文件系统的最顶层。
目录结构:从根目录延伸出来的各种目录,如“/home”、“/usr”等,以及它们的子目录。这些目录在树状结构中作为中间节点。
文件:这些是树结构的叶节点,表示实际的数据存储。
树结构的视觉表示
这两个系统中树的视觉表示帮助用户理解文件和目录之间的层级关系。用户可以轻松地浏览不同的目录层级,找到存储在不同位置的文件。
二叉树概念及结构
二叉树是计算机科学中的一种重要数据结构,具有以下特点:
基本定义
有限节点集合:二叉树是由节点组成的有限集合,这个集合可以为空,或者由一个根节点和两棵子树(左子树和右子树)构成。
空二叉树:如果这个集合为空,则称为一个空二叉树。
非空二叉树:包含一个根节点,以及可能为空的左子树和右子树,这两棵子树本身也是二叉树。
特点
度的限制:二叉树中不存在度大于2的节点。这意味着任何节点最多只有两个子节点:一个左子节点和一个右子节点。
有序性:二叉树的子树具有左右之分,且次序不能颠倒。因此,二叉树是一种有序树。
结构的多样性:任何二叉树都可以由更简单的二叉树通过添加左子树和/或右子树来构造。这表明二叉树具有递归的性质。
递归定义
二叉树的定义具有递归性质:一个二叉树的左子树和右子树本身也是二叉树。这种递归定义使得操作和算法设计在二叉树上可以高效实施。
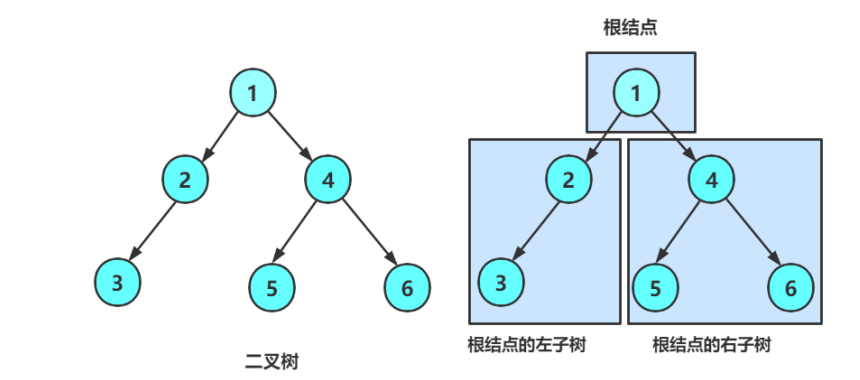
从上图可以看出:
1.二叉树不存在度大于2的结点
2二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
注意:对于任意的二叉树都是由以下几种情况复合而成的:

应用场景
二叉树在计算机科学中被广泛应用于多种场景,例如:
搜索树:如二叉搜索树,用于高效的数据搜索和访问。
堆结构:在优先队列和堆排序中使用。
哈夫曼树:在数据压缩算法中使用。
二叉树的性质
二叉树的性质
1.第i层的最大节点数:非空二叉树的第i层最多有 2^(i-1) 个节点(根节点层数为1)。
2.深度为h的二叉树的最大节点数:深度为h的二叉树最多有 2^h - 1 个节点。
3.叶节点和分支节点的关系:对任何非空二叉树,若叶节点数为n0,度为2的节点数为n2,则有 n0 = n2 + 1。
4.满二叉树的深度:具有n个节点的满二叉树的深度h为 ceil(log2(n+1))。
完全二叉树的节点关系:
->1.若i>0,则节点i的父节点为 (i-1)/2;若i=0,则i为根节点。
->若2i+1 < n,则节点i的左孩子为 2i+1;否则无左孩子。
->若2i+2 < n,则节点i的右孩子为 2i+2;否则无右孩子。
二叉树的存储结构
顺序存储
定义:使用数组来存储二叉树的节点。
适用性:适合完全二叉树,非完全二叉树会造成空间浪费。
物理和逻辑结构:物理上是数组,逻辑上是二叉树。
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空
间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆我们后面的章节会专门讲解。二叉树顺
序存储在物理上是一个数组,在逻辑上是一颗二叉树。
链式存储
二叉链:
Copy code
typedef int BTDataType;
struct BinaryTreeNode {
struct BinaryTreeNode* _pLeft; // 指向左孩子
struct BinaryTreeNode* _pRight; // 指向右孩子
BTDataType _data; // 节点值
};
三叉链:
struct BinaryTreeNode {
struct BinaryTreeNode* _pParent; // 指向父节点
struct BinaryTreeNode* _pLeft; // 指向左孩子
struct BinaryTreeNode* _pRight; // 指向右孩子
BTDataType _data; // 节点值
};
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是
链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所
在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链,后面课程
学到高阶数据结构如红黑树等会用到三叉链。

堆的概念及结构
堆是一种特殊的完全二叉树,主要用于实现优先队列。在堆中,每个节点的值都遵循特定的顺序规则,与其父节点的值有一定的关系。堆分为最大堆和最小堆两种类型:
最大堆(大根堆)
定义:堆中任意节点的值不小于其子节点的值。
特性:根节点是所有节点中的最大值。

最小堆(小根堆)
定义:堆中任意节点的值不大于其子节点的值。
特性:根节点是所有节点中的最小值。

存储方式
数组存储:堆通常使用数组来实现,按照完全二叉树的顺序存储方式存储在一维数组中。
堆的性质
节点顺序:堆中某个节点的值总是不大于(在最大堆中)或不小于(在最小堆中)其父节点的值。
完全二叉树:堆总是一棵完全二叉树,这意味着除了最底层,其他层都是满的,并且最底层的节点尽可能地集中在左侧。
操作
插入:将新元素添加到堆的末尾,然后向上调整以恢复堆的顺序。
删除(最大堆中删除最大元素,最小堆中删除最小元素):通常删除根节点,然后将最后一个元素移动到根节点位置,并向下调整以恢复堆的顺序。
结语
通过本文的探索,我们不仅理解了树和堆作为数据结构的基本特征和原理,而且还了解到了它们在现实世界中的应用。从理论到实践,树和堆展现了数据组织和处理的高效性与灵活性。无论是在软件开发、系统设计还是在解决复杂的编程问题中,这些知识都是不可或缺的。希望本文能激发您对数据结构更深入的兴趣,并在您的计算机科学旅程中起到助力作用。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 蔬菜网络销售平台(JSP+java+springmvc+mysql+MyBatis)
- vue3-Pinia
- 【分布式技术】监控平台zabbix对接grafana,优化dashboard
- springboot103抗疫物资管理系统
- Java中HashMap与HashTable的区别
- 基本定时器一启动就直接进中断的两种解决方式
- TeamViewer的安装教程和使用方法
- 汽车改装三维扫描抄数3d数据汽车整车上门数据测绘房车改装测量
- 开发利器——C语言必备实用第三方库
- 宿舍故障报修系统(JSP+java+springmvc+mysql+MyBatis)