CSP-S2019提高组day1-T2:括号树
题目链接
题目描述
本题中合法括号串的定义如下:
()是合法括号串。- 如果
A是合法括号串,则(A)是合法括号串。 - 如果
A,B是合法括号串,则AB是合法括号串。
本题中子串与不同的子串的定义如下:
- 字符串
S的子串是S中连续的任意个字符组成的字符串。S的子串可用起始位置 l l l 与终止位置 r r r 来表示,记为 S ( l , r ) S (l, r) S(l,r)( 1 ≤ l ≤ r ≤ ∣ S ∣ 1 \leq l \leq r \leq |S | 1≤l≤r≤∣S∣, ∣ S ∣ |S | ∣S∣ 表示 S 的长度)。 S的两个子串视作不同当且仅当它们在S中的位置不同,即 l l l 不同或 r r r 不同。
一个大小为 n n n 的树包含 n n n 个结点和 n ? 1 n - 1 n?1 条边,每条边连接两个结点,且任意两个结点间有且仅有一条简单路径互相可达。
小 Q 是一个充满好奇心的小朋友,有一天他在上学的路上碰见了一个大小为 n n n 的树,树上结点从 1 ~ n 1 \sim n 1~n 编号, 1 1 1 号结点为树的根。除 1 1 1 号结点外,每个结点有一个父亲结点, u u u( 2 ≤ u ≤ n 2 \leq u \leq n 2≤u≤n)号结点的父亲为 f u f_u fu?( 1 ≤ f u < u 1 ≤ f_u < u 1≤fu?<u)号结点。
小 Q 发现这个树的每个结点上恰有一个括号,可能是( 或)。小 Q 定义
s
i
s_i
si? 为:将根结点到
i
i
i 号结点的简单路径上的括号,按结点经过顺序依次排列组成的字符串。
显然 s i s_i si? 是个括号串,但不一定是合法括号串,因此现在小 Q 想对所有的 i i i( 1 ≤ i ≤ n 1\leq i\leq n 1≤i≤n)求出, s i s_i si? 中有多少个互不相同的子串是合法括号串。
这个问题难倒了小 Q,他只好向你求助。设
s
i
s_i
si? 共有
k
i
k_i
ki? 个不同子串是合法括号串, 你只需要告诉小 Q 所有
i
×
k
i
i \times k_i
i×ki? 的异或和,即:
(
1
×
k
1
)
?xor?
(
2
×
k
2
)
?xor?
(
3
×
k
3
)
?xor?
?
?xor?
(
n
×
k
n
)
(1 \times k_1)\ \text{xor}\ (2 \times k_2)\ \text{xor}\ (3 \times k_3)\ \text{xor}\ \cdots\ \text{xor}\ (n \times k_n)
(1×k1?)?xor?(2×k2?)?xor?(3×k3?)?xor???xor?(n×kn?)
其中
x
o
r
xor
xor 是位异或运算。
输入格式
第一行一个整数 n n n,表示树的大小。
第二行一个长为
n
n
n 的由( 与) 组成的括号串,第
i
i
i 个括号表示
i
i
i 号结点上的括号。
第三行包含 n ? 1 n ? 1 n?1 个整数,第 i i i( 1 ≤ i < n 1 \leq i \lt n 1≤i<n)个整数表示 i + 1 i + 1 i+1 号结点的父亲编号 f i + 1 f_{i+1} fi+1?。
输出格式
仅一行一个整数表示答案。
样例 #1
样例输入 #1
5
(()()
1 1 2 2
样例输出 #1
6
提示
【样例解释1】
树的形态如下图:
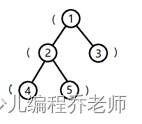
将根到 1 号结点的简单路径上的括号,按经过顺序排列所组成的字符串为 (,子串是合法括号串的个数为
0
0
0。
将根到 2 号结点的字符串为 ((,子串是合法括号串的个数为
0
0
0。
将根到 3 号结点的字符串为 (),子串是合法括号串的个数为
1
1
1。
将根到 4 号结点的字符串为 (((,子串是合法括号串的个数为
0
0
0。
将根到 5 号结点的字符串为 ((),子串是合法括号串的个数为
1
1
1。
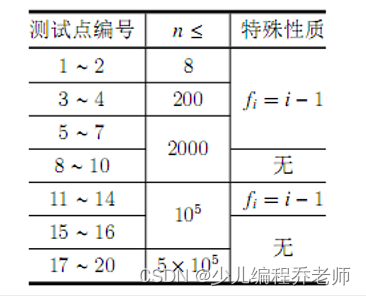
【数据范围】
算法思想
根据题目描述,要求的是树中从根结点到 i i i 号结点组成的括号串 s i s_i si?中,合法括号串的个数。示例参考提示【样例解释1】。
对于任意括号串
s
i
s_i
si?如下图所示:

要计算括号串
s
i
s_i
si?中合法括号串的个数,不妨设为
f
(
i
)
f(i)
f(i),从最后一步分析,也就是根据
i
i
i号结点的选择分成两种情况:
- 不选择 i i i号结点,那么方案数等于括号串 s i ? 1 s_{i-1} si?1?中合法括号串的个数,即 f ( i ? 1 ) f(i-1) f(i?1)
- 选择
i
i
i号结点(前提是
i
i
i号结点是
)),那么以 i i i结尾的合法括号串的个数如何计算呢,不妨设其为 g ( i ) g(i) g(i):- 首先找到与
i
i
i号结点匹配的
(的位置,不妨设为 j j j(如上图所示),那么从 j j j到 i i i就是一组合法的括号串 - 其次考虑 j j j之前合法括号串的个数,即以 j ? 1 j-1 j?1结尾的合法括号串的个数,就是 g [ j ? 1 ] g[j-1] g[j?1],
- 可得以 i i i结尾的合法括号串的个数,就是在以 j ? 1 j-1 j?1结尾的合法括号串后添加了 1 1 1组,即 g [ i ] = g [ j ? 1 ] + 1 g[i]=g[j-1]+1 g[i]=g[j?1]+1
- 首先找到与
i
i
i号结点匹配的
那么,
f
(
i
)
=
f
(
i
?
1
)
+
g
[
i
]
f(i)=f(i-1)+g[i]
f(i)=f(i?1)+g[i],其中
g
[
i
]
g[i]
g[i]表示以
i
i
i结尾的合法括号串的个数,
g
[
i
]
=
g
[
j
?
1
]
+
1
g[i]=g[j-1]+1
g[i]=g[j?1]+1,
j
j
j是与
i
i
i匹配的左括号(的位置。
进一步分析,以 j ? 1 j-1 j?1结尾的合法括号串的个数 g [ j ? 1 ] g[j-1] g[j?1],其实就是从根节点到 j ? 1 j-1 j?1号结点的所有合法括号串中去掉不选择 j ? 1 j-1 j?1号结点的方案数,即 g ( j ? 1 ) = f ( j ? 1 ) ? f ( j ? 2 ) g(j-1)=f(j-1)-f(j-2) g(j?1)=f(j?1)?f(j?2)
综上所述,
f
(
i
)
=
f
(
i
?
1
)
+
f
(
j
?
1
)
?
f
(
j
?
2
)
+
1
f(i)=f(i-1)+f(j-1)-f(j-2)+1
f(i)=f(i?1)+f(j?1)?f(j?2)+1,其中
j
j
j是与
i
i
i匹配的左括号(的位置。
通过上面的分析,要想进行计算还要解决两个问题:
- 在树上如何得到括号串 i i i位置的上一个结点 i ? 1 i-1 i?1?
在树上 i i i位置的上一个结点,就是 i i i的父节点,可以设置一个数组
p[i]来存储i的父节点
- 如何得到与
i
i
i匹配的左括号
(的位置 j j j?
括号匹配,可以通过栈来实现。如果
i位置是左括号,直接入栈,如果i位置是右括号,则栈顶就是与之匹配的左括号的位置。
下面从动态规划的角度将上述分析整理一下。
状态表示
- f [ i ] f[i] f[i]表示树中从根结点到 i i i 号结点组成的括号串 s i s_i si?中合法括号串的个数
最终答案
=
(
1
×
f
[
1
]
)
?xor?
(
2
×
f
[
2
]
)
?xor?
(
3
×
f
[
3
]
)
?xor?
?
?xor?
(
n
×
f
[
n
]
)
= (1 \times f[1])\ \text{xor}\ (2 \times f[2])\ \text{xor}\ (3 \times f[3])\ \text{xor}\ \cdots\ \text{xor}\ (n \times f[n])
=(1×f[1])?xor?(2×f[2])?xor?(3×f[3])?xor???xor?(n×f[n])。注意
n
n
n的范围很大(
n
≤
5
×
1
0
5
n\le5\times10^5
n≤5×105),会爆int。
状态计算
从最后一步分析,根据 i i i号结点的选择分成两种情况:
- 不选择 i i i号结点,那么方案数等于括号串 s i ? 1 s_{i-1} si?1?中合法括号串的个数,即 f [ p [ i ] ] f[p[i]] f[p[i]],其中 p [ i ] p[i] p[i]表示 i i i的父结点,也就是括号串中 i i i之前的结点
- 选择
i
i
i号结点(前提是
i
i
i号结点是
)),先找到与 i i i匹配的左括号的位置 j j j,其父节点为 p [ j ] p[j] p[j],那么以以 i i i结尾的合法括号串的个数为 f [ p [ j ] ] ? f [ p [ p [ j ] ] ] + 1 f[p[j]]-f[p[p[j]]]+1 f[p[j]]?f[p[p[j]]]+1。
那么, f [ i ] = f [ p [ i ] ] + f [ p [ j ] ] ? f [ p [ p [ j ] ] ] + 1 f[i]=f[p[i]]+f[p[j]]-f[p[p[j]]]+1 f[i]=f[p[i]]+f[p[j]]?f[p[p[j]]]+1。
初始状态
根节点编号为 1 1 1,根结点自己组成的合法括号串的个数为 0 0 0,即 f [ 1 ] = 0 f[1]=0 f[1]=0。
时间复杂度
- 状态数为 n n n
- 每个结点的状态只会计算一次,时间复杂度 O ( 1 ) O(1) O(1)
总的时间复杂度为 O ( n ) O(n) O(n)。
代码实现
#include <iostream>
#include <vector>
using namespace std;
const int N = 5e5 + 10;
typedef long long LL;
char s[N];
int p[N], stk[N], top;
//f[i]表示树中从根结点到i号结点组成的括号串中合法的方案数
LL f[N];
vector<int> g[N]; //邻接表
void dfs(int i)
{
if(s[i] == '(')
{
stk[++ top] = i; //左括号入栈
f[i] = f[p[i]]; //不选择i号结点
for(int k : g[i])
dfs(k); //递归处理子结点
top --; //回溯,恢复现场
}
else //右括号
{
if(top == 0) //栈空,没有与之匹配的左括号
{
f[i] = f[p[i]]; //不选择i号结点
for(int k : g[i])
dfs(k); //递归处理子结点
}
else
{
int j = stk[top --]; //从栈顶取出与i匹配的右括号位置
f[i] = f[p[i]] + f[p[j]] - f[p[p[j]]] + 1; //状态计算
for(int k : g[i])
dfs(k); //递归处理子结点
stk[++ top] = j; //回溯,恢复现场
}
}
}
int main()
{
int n;
scanf("%d%s", &n, s + 1);
for(int i = 2; i <= n; i ++)
{
scanf("%d", &p[i]); //输入i的父结点
g[p[i]].push_back(i); //将i添加到a的子结点中
}
dfs(1);
LL ans = 0;
for(int i = 1; i <= n; i ++) ans ^= i * f[i];
printf("%lld\n", ans);
return 0;
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 基于PyQT的图片批处理系统
- Docker:Docker集群配置与应用(Docker Swarm)
- 【日常记录】自动化部署与持续交付:GitHub Actions CICD
- 卡尔曼滤波学习笔记
- 1、分布式系统的一致性与共识性
- 喜好儿AI周报Weekly(第9期)CES2024 AI产业大爆发 | Rabbit R1 | 3D-Fauna | OLED屏幕 | Genie | MagicVideoV2 | Magnific
- 四川思维跳动商务信息咨询有限公司电商服务怎么样
- LiveSIPB流媒国网B接口功能-国网B接口服务安装使用说明
- 【数据结构】顺序表
- 搭建Python环境