机器学习之过拟合与欠拟合，K折交叉验证详解【含代码】

欠拟合

欠拟合（Underfitting）是机器学习和统计学中的一个术语，描述了模型在训练数据和新数据（如测试数据或验证数据）上都表现不佳的情况。换句话说，欠拟合的模型没有足够地“学习”或“捕捉”数据中的模式和结构。

欠拟合的主要特征和原因包括：

• 模型过于简单：例如，尝试使用线性模型来拟合非线性数据。

• 训练时间不足：对于需要长时间训练的模型（如深度学习模型），如果训练时间太短，模型可能没有足够的机会学习数据的特征。

• 不足够的特征：如果只使用了部分相关特征进行训练，或者提取的特征无法很好地代表数据，模型可能会出现欠拟合。

• 模型参数设置不当：例如，决策树的最大深度设置得太浅，或正则化参数设置得过高。

如何检测和解决欠拟合：

检查模型在训练和测试数据上的性能：欠拟合的模型通常在这两者上都会表现得不太好。

选择更复杂的模型：如果使用的是简单模型，考虑使用更复杂的模型或添加更多的特征。

增加特征：添加更多的特征，或者使用特征工程方法来构造新的特征。

减少正则化：如果使用了正则化技术（如L1或L2正则化），可以考虑减少正则化强度或完全去掉。

增加训练时间：对于需要长时间训练的模型，增加迭代次数或训练时间。

获取更多的数据：有时，数据太少，无法充分代表整体分布，增加更多的训练数据可以有助于改善模型的性能。

总的来说，欠拟合意味着模型没有足够地学习数据，解决的关键通常是使模型更加复杂或为其提供更多的信息。

过拟合

过拟合（Overfitting）是机器学习中的一个常见问题，描述的是模型过度地“学习”训练数据，包括其中的噪声和异常值，从而导致其在新的、未见过的数据上表现不佳。

过拟合的主要特征和原因包括：

• 模型过于复杂：例如，拥有大量参数的深度神经网络，或深度很深的决策树。

• 训练数据量不足：与模型的复杂性相比，如果训练数据不足，模型可能会过度拟合。

• 数据噪声：如果训练数据包含错误或噪声，模型可能会尝试拟合这些噪声。

• 不必要的特征：如果包含许多与目标输出无关的特征，它们可能会导致过拟合。

如何检测和解决过拟合：

训练/验证曲线：通过观察模型在训练和验证数据上的性能，可以发现过拟合。特征是：训练误差低，但验证误差高。

交叉验证：使用交叉验证来估计模型在新数据上的性能。

正则化：使用L1或L2正则化可以约束模型的复杂性，并防止过拟合。

简化模型：选择一个简化版本的模型，例如，减少神经网络的层数或神经元数量，或限制决策树的深度。

早停：在训练深度学习模型时，当验证误差不再减少或开始增加时，停止训练。

数据增强：对训练数据进行小的修改以创建新的训练样本。这在图像识别任务中尤其有效。

丢弃法（Dropout）：在训练深度学习模型时，随机丢弃一些神经元，可以作为正则化手段，减少过拟合。

增加训练数据：如果可能的话，获取更多的训练数据可以帮助减少过拟合。

特征选择：通过选择与目标输出最相关的特征，可以减少模型的复杂性。

总的来说，过拟合意味着模型在训练数据上表现得太好，以至于失去了泛化到新数据上的能力。解决过拟合的关键是平衡模型的复杂性与其在训练数据上的性能，同时考虑到其在未见过的数据上的性能。

权重衰退通常与L2正则化（Ridge正则化）等价。事实上，上面的惩罚项实际上就是L2范数正则化。当我们讨论权重衰退时，我们通常指的是在深度学习模型中添加L2正则化。

K折交叉验证

1. 基本概念：

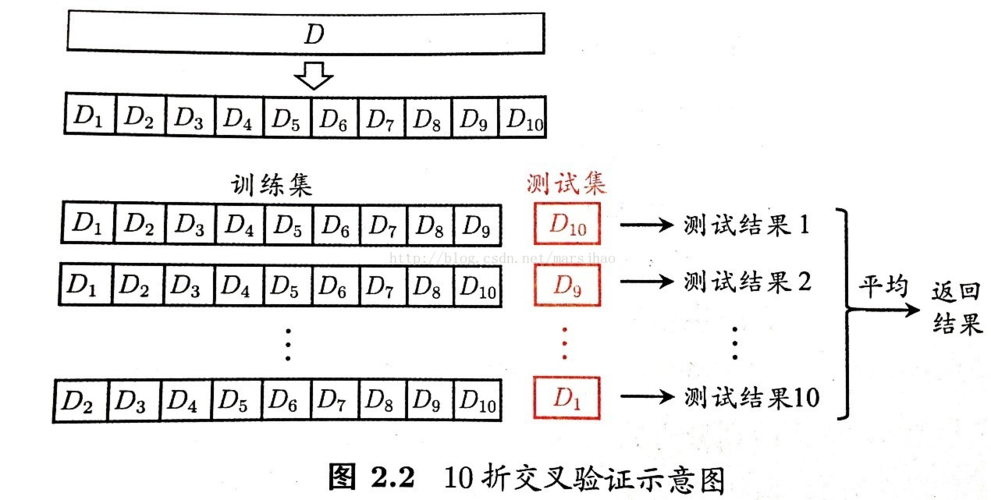
K折交叉验证是一种评估模型性能的方法。在这种方法中，训练数据被分割为K个子集（或称为“折”）。每次迭代，其中一个子集被用作测试集，而其他K-1个子集组合成训练集。这个过程会重复K次，每个子集都有一次机会作为测试集。最后，得到的K个模型的评估指标（如准确率）的平均值被用作总体的模型评估。
2. 步骤：

数据分割：将整个数据集随机分割成K个大小大致相同的非重叠子集。
模型训练与评估：对于每一折：
    将这一折作为测试集，其余的K-1折组合作为训练集。
    使用训练集训练模型。
    使用测试集评估模型。
    记录评估指标。
计算平均指标：计算K次评估得到的指标的平均值。这个平均值被用作模型的整体评估指标。

3. 优点：

   减少偶然性：因为每个数据点都有机会出现在训练集和测试集中，所以K折交叉验证提供了一个关于模型性能更稳健的估计。
   利用数据：尤其在数据较少的情况下，K折交叉验证能够更充分地利用可用数据进行模型训练与评估。

4. 缺点：

   计算成本：需要训练K次模型，所以计算成本高于简单的数据分割方法。
   不适用于所有数据分布：如果数据集有特定的结构或分布，可能需要使用分层K折交叉验证或其他变种。

5. 变体：

   分层K折交叉验证（Stratified K-Fold）：在每个折中，每个类的数据比例与整体数据集中的比例大致相同。这在类分布不均匀的情况下尤其有用。
   时间序列交叉验证：对于时间序列数据，确保训练集中的时间点始终早于测试集中的时间点。

6. 使用场景：

   模型评估：评估单一模型的性能。
   模型选择：在不同的模型或算法之间进行选择。
   参数调优：找到模型的最佳参数设置。

总之，K折交叉验证是一种评估和改进模型性能的强大工具，它可以帮助研究者或数据科学家在训练过程中避免过拟合，从而建立一个更泛化的模型。

利用网格搜索和K折交叉验证优化参数

# 导入所需库
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV, train_test_split
from sklearn.metrics import accuracy_score

# 加载数据
data = load_iris()
X = data.data
y = data.target

# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 设置随机森林的参数范围
param_grid = {
    'n_estimators': [10, 50, 100, 150],
    'max_depth': [None, 10, 20, 30],
    'min_samples_split': [2, 5, 10],
    'min_samples_leaf': [1, 2, 4],
    'bootstrap': [True, False]
}

# 初始化随机森林分类器
rf = RandomForestClassifier()

# 使用GridSearchCV进行网格搜索与K折交叉验证
grid_search = GridSearchCV(estimator=rf, param_grid=param_grid, 
                           cv=5, n_jobs=-1, verbose=2)

# 拟合模型
grid_search.fit(X_train, y_train)

# 获取最佳参数
best_params = grid_search.best_params_
print("最佳参数:", best_params)

# 使用最佳参数的模型进行预测
best_rf = grid_search.best_estimator_
y_pred = best_rf.predict(X_test)

# 计算并输出准确度
accuracy = accuracy_score(y_test, y_pred)
print("测试集准确度:", accuracy)

当网格搜索完成后，你可以使用best_params_属性获取最佳的参数组合，并使用best_estimator_获取相应的模型。

但是这种有时候计算资源非常大，而且效果不好，无法达到最优，有时候也是劣势的局部最优，这类情况如果是有参数的一个确定的范围数值之后，可以采取。

所以一般我喜欢采取单个的参数进行寻优，逐步的优化，在单个参数达到我们定义的空间的局部最优的时候，在进行下一步

K折交叉验证不仅仅适用于多参数的网格搜索，也适用于单个参数的调优。其目的是为了提供对模型在未见数据上性能的一个更稳健的估计，从而帮助我们选择更好的参数。

from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
import numpy as np

# 加载数据
data = load_iris()
X = data.data
y = data.target

# 对不同的n_estimators值进行交叉验证
n_estimators_options = [10, 50, 100, 150, 200]
for n_estimators in n_estimators_options:
    rf = RandomForestClassifier(n_estimators=n_estimators)
    scores = cross_val_score(rf, X, y, cv=5)
    print(f'n_estimators: {n_estimators}, 交叉验证平均准确率: {np.mean(scores)}')

之后，你就可以采取取平均值，用来判断参数的最佳值是多少

一般而言，交叉验证在参数优化和模型的评估用的比较多

每文一语

适应中学习