蚁群算法的应用——求解二元函数的极值

仅作自己学习使用

---

1 蚁群算法相关知识点

1.1 蚁群算法的特点

• 蚁群算法是一种模拟蚂蚁寻找食物的过程的仿生优化算法，理由是蚂蚁有能力在没有任何提示的情况下找到从巢穴到事物源的最短路径，并且能随环境的变化，适应性地搜索新的路径，产生新的路径选择。
• 在蚂蚁搜索过程中，有一个重要的物质信息素，这是蚂蚁之间进行信息交换的主要途径。蚂蚁在搜索的过程中，会在走过的路径上留下信息素，路径上的信息素会随着时间地推移而逐渐地蒸发，而单只蚂蚁能够携带的信息素总量是确定的，因此同一只蚂蚁，选择长的路径会导致长的路径上的平均信息素浓度比短的路径更低。后来的蚂蚁在选择某条路径的概率与它感知到的路径上的信息素浓度有关，蚂蚁会选择它面临的几条路径上信息素浓度最高的那条路径。因此当一条路径上通过的蚂蚁越来越多时，该条路径上的信息素浓度也越来越高，从而以后的蚂蚁选择该条路径的概率就更高，又会导致该条路径上通过的蚂蚁数量更多，从而使信息素浓度更高，这就是蚁群算法中一个重要的机制——正反馈机制，在这样一个机制的运作下，最终可以找到从巢穴到事物源的最短路径。
  
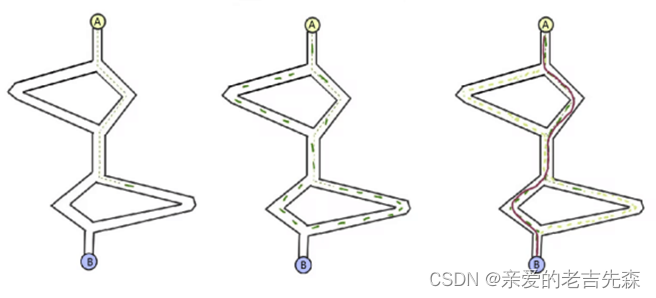
  如图所示：蚁群从A到B事先并不知道哪条路径最优，所以在第一次搜索时，每条路径都有机会被搜索到，一段时间后，距离较远路径上的信息素残留越来越少，而距离最近路径上的信息素越来越密，直到最后找到一条最优路径时，算法结束。
• 蚁群算法具有分布式计算、无中心控制和分布式个体之间间接通信的特征。
• 蚁群算法是一种本质上的并行算法。对于人工蚂蚁，每只蚂蚁搜索的过程彼此独立，仅通过信息激素进行通信，所以蚁群算法可以看作是一个分布式的多智能体系统，这使得算法具有较强的全局搜索能力。

1.2 人工蚁群算法的优化过程

• 相较真实蚂蚁，人工蚁群具有一定的记忆能力，记得自己走过的路径。
• 人工蚁群释放的信息素的数量使其生成解的质量的函数，也就是说解的质量与信息素浓度有关
  ????????以旅行商问题（TSP）为例，假设m只蚂蚁在图的相邻节点间移动，从而协作异步地得到问题的解。每只蚂蚁的一步转移概率由图中的每条边上的两类参数决定：一是信息素含量（τ,tao），也称为信息素痕迹；而是能见度，即先验函数值(η)。
  ????????信息素的更新方式有两种：一是挥发，也就是所有路径上的信息素以一定的比率减少，模拟自然界信息素随时间挥发的过程；二是增强，给具有给优秀的边增加一定浓度的信息素。
  ????????蚂蚁向下一个目标的运动是通过一个随机原则来实现的（类似于遗传算法中的轮盘赌选择算子），利用当前节点存储的信息，计算下一步可达节点的概率，并按此概率来选择下一步节点。
• 在算法的初始时刻，将m只蚂蚁随机地放到n座城市，同时将m只蚂蚁的禁忌表tabu的第一个元素设置为它当前所在的城市。此时各路径上的信息素浓度相同，将0时刻各条路径上的信息素浓度都给一个相同的较小的常数，接下来，每只蚂蚁根据路径上残留的信息素浓度和启发式信息（两个节点间的距离）独立地选择下一座城市：
  

1.3 算法流程图

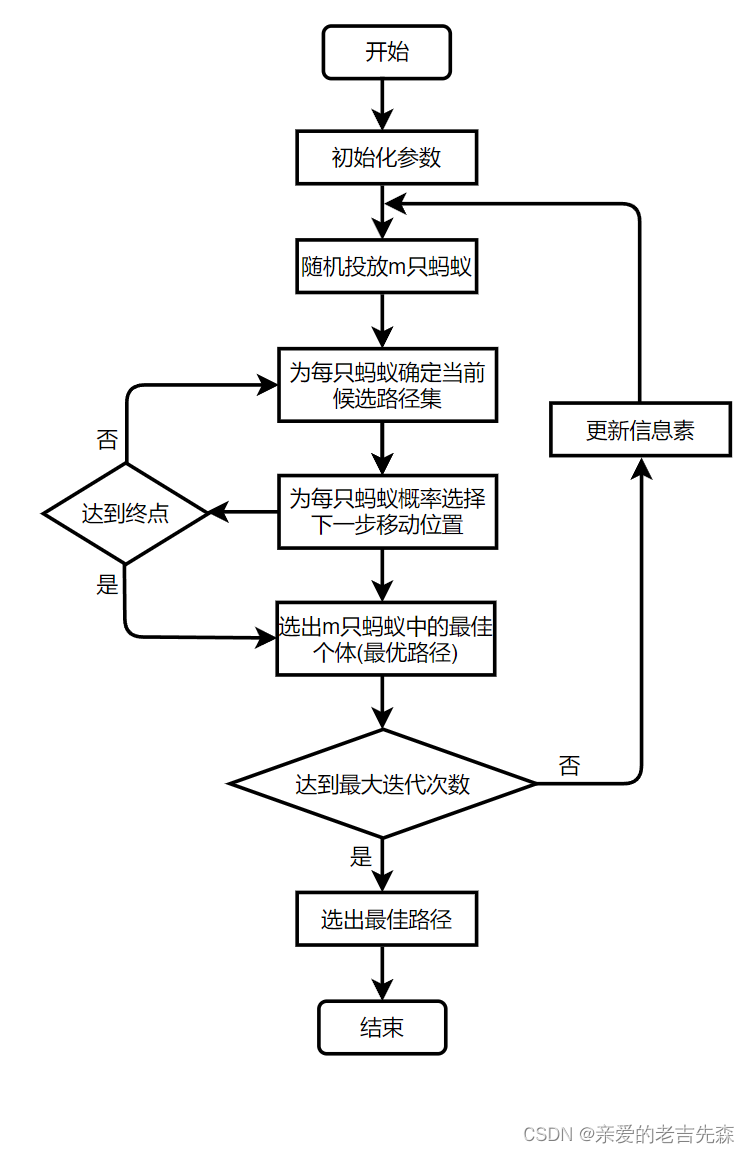
2 问题

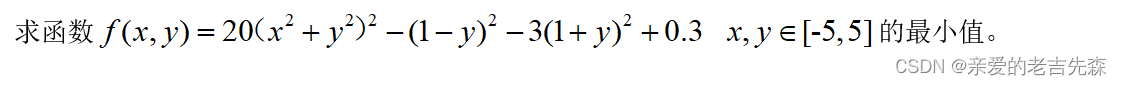
函数的图像：

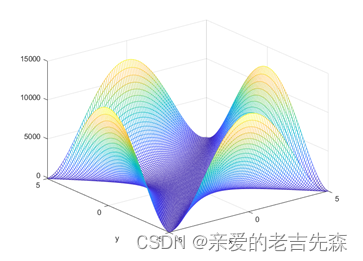
3 MatLab代码

%% 利用蚁群算法（ACO)求解函数的最小值
% f(x,y) = 20*(x^2 - y^2)^2 - (1-y)^2 - 3*(1+y)^2 + 0.3;

clear
clc
m = 20;     % 蚂蚁数量
G = 200;    % 最大迭代次数
rho = 0.8;  % 信息素蒸发程度
p0 = 0.2;   % 转移概率常数
xMax = 5;   % 搜索x的最大值
xMin = -5;  % 搜索x的最小值
yMax = 5;   % 搜索y的最大值
yMin = -5;  % 搜索y的最小值
X = zeros(m,2);     % m只蚂蚁的初始位置
tau = zeros(m,1);   % 每只蚂蚁的适应度值（函数值）
trace = zeros(G,1); % 每代蚂蚁的最优适应度
for i = 1:m
    X(i,1) = (xMin + (xMax - xMin)*rand);
    X(i,2) = (yMin + (yMax - yMin)*rand);
    tau(i) = GetTau(X(i,1),X(i,2));
end
step = 1;           % 局部搜索步长
P = zeros(G,m);     % 每代中各只蚂蚁的状态转移概率
for NC = 1:G
    lambda = 1/NC;  % ?
    [Tau_best,BestIndex] = min(tau);  % Tau_best：最小的函数值；BestIndex：最小的函数值对应的蚂蚁编号
    %% 计算状态转移概率（根据当前这代蚂蚁中最优的适应度值更新本代蚂蚁中的状态转移概率） 
    for i = 1:m
        P(NC,i) = (Tau_best-tau(i))/Tau_best;
    end
    %% 更新每只的位置
    for i = 1:m
        if P(NC,i) < p0
            % 局部搜索
            temp1 = X(i,1) + (2*rand-1)*step*lambda;
            temp2 = X(i,2) + (2*rand-1)*step*lambda;
        else
            % 全局搜索
            temp1 = X(i,1) + (xMax-xMin)*(rand-0.5);
            temp2 = X(i,2) + (xMax-xMin)*(rand-0.5);
        end
        %% 边界处理
        if temp1 < xMin
            temp1 = xMin;
        end
        if temp1 > xMax 
            temp1 = xMax;
        end
        if temp2 < yMin
            temp2 = yMin;
        end
        if temp2 < yMax
            temp2 = yMax;
        end
        %% 判断蚂蚁当前位置的状态是否更优
        if GetTau(temp1,temp2) < GetTau(X(i,1),X(i,2))
            X(i,1) = temp1;
            X(i,2) = temp2;
        end
    end
    %% 更新信息素
    for i = 1:m
        tau(i) = (1-rho)*tau(i) + GetTau(X(i,1),X(i,2));
    end
    [value,index] = min(tau);
    trace(NC) = GetTau(X(index,1),X(index,2));
end
[minValue,minIndex] = min(tau);
minX = min(minIndex,1);
minY = min(minIndex,2);
figure(color=[1 1 1])
plot(trace,LineWidth=2,Color=[1, 0.6, 0]);
title("适应度进化曲线")
xlabel('搜索次数')
ylabel("适应度值")

%% 绘图
figure(color=[1 1 1])
X = -5:0.1:5;
Y = -5:0.1:5;
N = length(X);
for i = 1:N
    for j = 1:N
        Z(i,j) = 20*(X(i)^2 - Y(j)^2)^2 - (1-Y(j))^2 - 3*(1+Y(j))^2 + 0.3;
    end
end
colormap parula
mesh(X,Y,Z)
xlabel("x");
ylabel("y");
hold on
scatter3(minX, minY, GetTau(minX,minY), 50, 'r', 'filled'); 
hold off;
%% 适应度函数
function fxy = GetTau(x,y)
    fxy = 20*(x^2 - y^2)^2 - (1-y)^2 - 3*(1+y)^2 + 0.3;
end

4 效果图

4.1 最小值在函数图像中

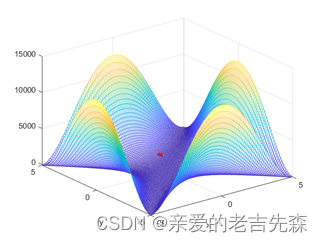图中红色的点就是找到的最小值点。

4.2 历代迭代图

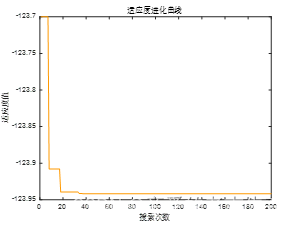
5 总结

%% TODO