向量投影:如何将一个向量投影到矩阵的行向量生成子空间?
向量投影:如何将一个向量投影到矩阵的行向量生成子空间?
前言
本问题是在学习Rosen梯度投影优化方法的时候遇到的问题,主要是对于正交投影矩阵(NT(NNT)-1N)的不理解,因此经过查阅资料,学习了关于向量投影的知识,记录如下。
首先需要了解 子空间和子空间的正交补。相关知识可以查阅本人的另外一篇笔记,核和值域的关系:什么是矩阵的秩?,这篇笔记中是以矩阵列向量的生成子空间为例展开的。
核心公式:
- R ( A H ) ∩ N ( A ) = { 0 } R(A^H) \cap N(A)=\{0\} R(AH)∩N(A)={0}
- R ( A H ) ⊕ N ( A ) = C m R(A^H) \oplus N(A) = C^m R(AH)⊕N(A)=Cm
其中R(AH)是A的行向量的生成子空间, R ( A H ) = { y ∈ R n ∣ y = A H x , x ∈ C m } R(A^H)=\{y\in R^n|y=A^Hx,x\in C^m\} R(AH)={y∈Rn∣y=AHx,x∈Cm}。
N(A)是A的核子空间, N ( A ) = { x ∣ A x = 0 , x ∈ R n } N(A)=\{x|Ax=0,x\in R^n\} N(A)={x∣Ax=0,x∈Rn}。
正文
所谓向量投影,本质上是期望将Rn空间中的任意一个n维向量,分解称为y1+y2,其中y1属于R(AH),y2属于N(A)。
1、投影矩阵
投影是一种线性变换,要求两次投影变换的结果等于一次投影变换的结果。在信号处理领域当中,一个信号经过两次滤波器和经过一次滤波器的结果是相等的,那么这个滤波器在数学上可抽象成一个投影矩阵。
写成数学公式: P 2 x = P P x = P x P^2x=PPx=Px P2x=PPx=Px。因此要求投影矩阵P是一个方阵。
可证明:R§=R(PH)。通常情况下一个方阵的行空间和列空间是不相同的,二者仅仅是同构关系,即维数相同。
即: R ( P ) ⊕ N ( P ) = C n R(P) \oplus N(P) = C^n R(P)⊕N(P)=Cn
投影分为正交投影和斜投影。二者的区别在于,正交投影矩阵P,R§的正交补=N§,等价于,R§和N§正交。而斜投影矩阵则没有这个性质。
可证明:一个投影矩阵P,是正交投影矩阵的充要条件是:P=PH
举一个简单的例子。
R2空间,向x轴的正交投影P,只能是取一个二维向量的横坐标。R§就是x轴,N§就是y轴,x轴的正交补是y轴。
R2空间,向x轴的斜投影Q,比如是指向东偏南45度?方向的的投影。R(Q)就是x轴,x轴的正交补是y轴,而N(Q)是沿着东偏南45度?方向的一维子空间,即N(Q)={ x|x = a(1,-1)T, a \in R}。
2、如何将一个向量投影到行满秩矩阵A的行向量生成子空间?
现在已知一个行满秩矩阵 A m m × n A^{m\times n}_m Amm×n?,R(AH)是由A的行向量生成的子空间。由上面的例子,可以猜到,n维欧氏空间向R(AH)的正交投影是唯一的,斜投影是不唯一的(此处考虑典型情况,而非考虑A行列满秩的极端情况)。
现在推导一个由A构成的正交投影矩阵P。
- y = y 1 + y 2 , y 1 ∈ R ( A H ) , y 2 ∈ R ⊥ ( A H ) y=y_1+y_2,y_1\in R(A^H),y_2\in R^\perp(A^H) y=y1?+y2?,y1?∈R(AH),y2?∈R⊥(AH)
- P y = P ( y 1 + y 2 ) = y 1 Py=P(y_1+y_2)=y_1 Py=P(y1?+y2?)=y1?
- y 1 ∈ R ( A H ) , ∴ y 1 = A H x y_1\in R(A^H),\therefore y_1=A^Hx y1?∈R(AH),∴y1?=AHx,x是一个m维的列向量,即y1可表示为A的行向量的线性组合
- y 2 ∈ R ⊥ ( A H ) = N ( A ) , A y 2 = 0 , A y = A A H x y_2\in R^\perp(A^H)=N(A),Ay_2=0,Ay=AA^Hx y2?∈R⊥(AH)=N(A),Ay2?=0,Ay=AAHx
- x = ( A A H ) ? 1 A y , y 1 = [ A H ( A A H ) ? 1 A ] y x=(AA^H)^{-1}Ay,y_1 = [A^H(AA^H)^{-1}A]y x=(AAH)?1Ay,y1?=[AH(AAH)?1A]y
- P = A H ( A A H ) ? 1 A = P H P = A^H(AA^H)^{-1}A=P^H P=AH(AAH)?1A=PH
从第5步可以知道为什么需要A行满秩了,只有行满秩的矩阵, y 1 ∈ R ( A H ) , y 1 = A H x y_1\in R(A^H),y_1=A^Hx y1?∈R(AH),y1?=AHx,其中x才有唯一解。
至此,我们知道 P = A H ( A A H ) ? 1 A P = A^H(AA^H)^{-1}A P=AH(AAH)?1A是一个正交投影矩阵,将一个向量投影到A的行向量的生成子空间。
3、关于Rosen梯度投影法
Rosen梯度投影法的可行下降方向: P k = Q ( ? g k ) = ( I ? N T ( N N T ) ? 1 N ) g k P^k = Q(-g^k) = (I-N^T(NN^T)^{-1}N)g^k Pk=Q(?gk)=(I?NT(NNT)?1N)gk
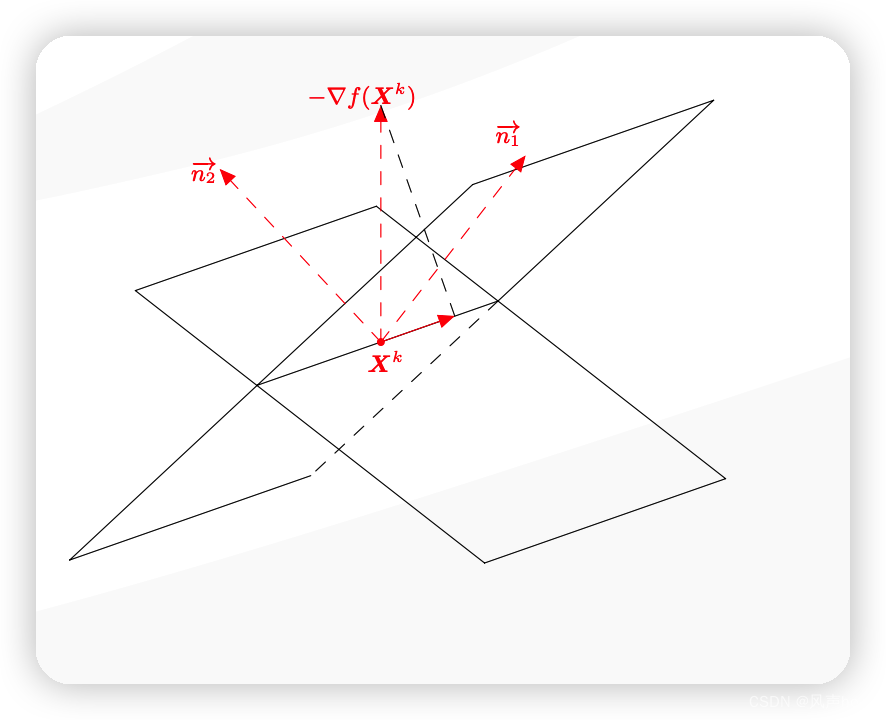
Q是一个投影矩阵,并且投向 N T ( N N T ) ? 1 N N^T(NN^T)^{-1}N NT(NNT)?1N的正交补空间,N是由积极约束的法向量组成的矩阵,因此P是负梯度方向向积极约束的法向量张成的行空间的正交补的投影。从几何上看,就是将负梯度方向投影向了积极约束的超平面的交线上。
需要注意,Rosen梯度投影法的约束条件是一个多面集。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Self-correcting LLM-controlled Diffusion Models
- 第22集《佛法修学概要》
- 介绍一个在线K8S练习平台
- Python:优雅的格式化XML美化输出格式
- nodeJS搭建免费代理IP池爬取贴吧图片实战
- 基于ChatGPT4+Python近红外光谱数据分析及机器学习与深度学习建模
- 备战2个月,面试被问麻了....
- Java重修第一天—学习数组
- 微信小程序---全局数据共享
- unity C# 中一看就会的try-catch-finally、throw