代码随想录第三十五天（一刷&&C语言）|整数拆分&&不同的二叉搜索树

创作目的：为了方便自己后续复习重点，以及养成写博客的习惯。

一、整数拆分

思路：参考carl文档。

1、确定dp数组以及下标的含义：分拆数字i，可以得到的最大乘积为dp[i]。

2、确定递推公式：从1遍历j，dp[i]可以由j * (i - j) 直接相乘。也可以由j * dp[i - j](相当于是拆分(i - j))得到。dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j))。

3、dp数组的初始化：初始化dp[2] = 1，从dp[i]的定义来说，拆分数字2，得到的最大乘积是1。

拆分0与1是无意义的。

4、确定遍历的方向：由递推公式知遍历方向为从左到右。

5、举例n为某个数的时候，推到dp数组。

ledcode题目：https://leetcode.cn/problems/integer-break/

AC代码：

//初始化DP数组
int *initDP(int num) {
    int* dp = (int*)malloc(sizeof(int) * (num + 1));
    int i;
    for(i = 0; i < num + 1; ++i) {
        dp[i] = 0;
    }
    return dp;
}

//取三数最大值
int max(int num1, int num2, int num3) {
    int tempMax = num1 > num2 ? num1 : num2;
    return tempMax > num3 ? tempMax : num3;
}

int integerBreak(int n){
    int *dp = initDP(n);
    //初始化dp[2]为1
    dp[2] = 1;

    int i;
    for(i = 3; i <= n; ++i) {
        int j;
        for(j = 1; j < i - 1; ++j) {
            //取得上次循环:dp[i]，原数相乘，或j*dp[]i-j] 三数中的最大值
            dp[i] = max(dp[i], j * (i - j), j * dp[i - j]);
        }
    }
    return dp[n];
}

二、不同的二叉搜索树

思路：参考carl文档。

1、确定dp数组及其下标的含义：1到i为节点组成的二叉搜索树的个数为dp[i]。

2、确定递推公式：dp[i] += dp[j - 1] * dp[i - j]?，j-1 为j为头结点左子树节点数量，i-j 为以j为头结点右子树节点数量。

3、dp数组的初始化：空节点也是一棵二叉树，也是一棵二叉搜索树。初始化dp[0] = 1。并且防止左右子树相乘出现0值的情况。

4、确定遍历方向：由递推公式知，节点数为i的状态依靠于 i之前节点数的状态。故遍历i里面每一个数作为头结点的状态，用j来遍历。

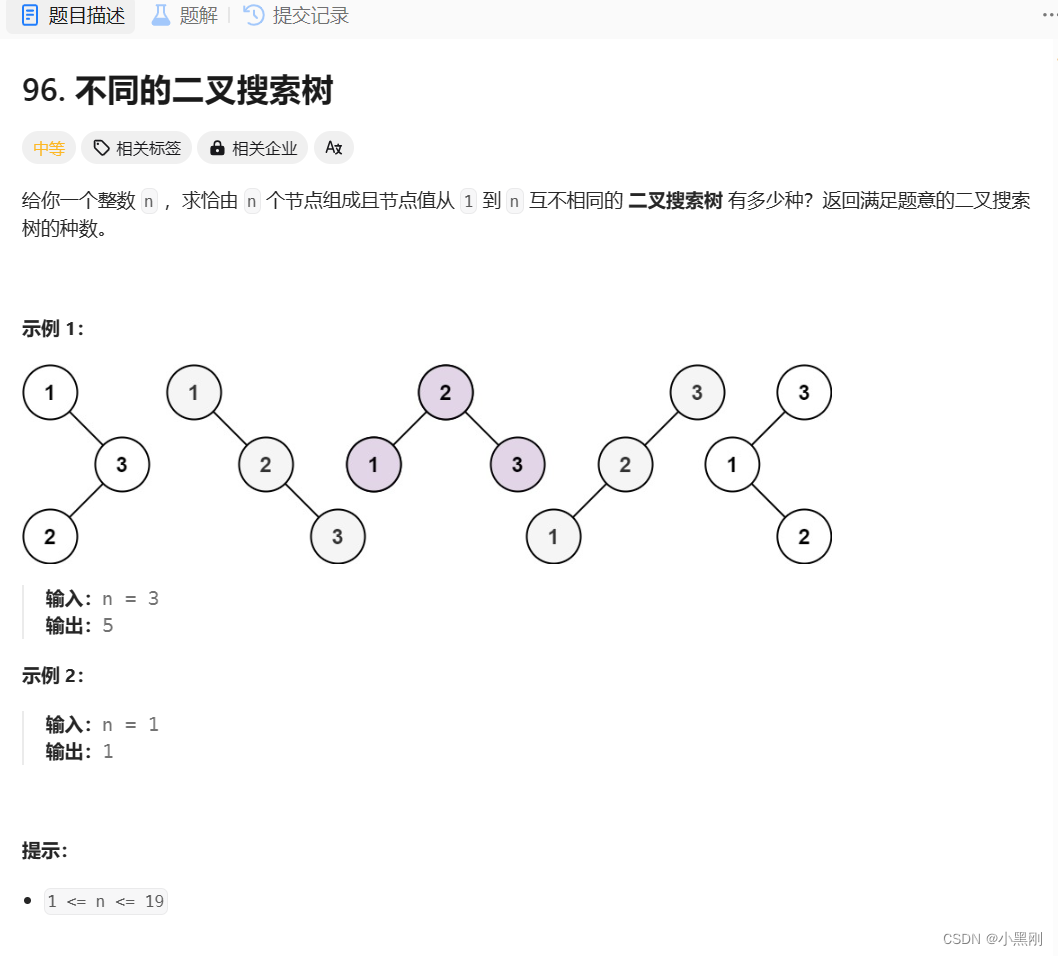
5、举例n为某个数的时候dp数组的状态。

lecode题目：https://leetcode.cn/problems/unique-binary-search-trees/description/

AC代码：

//开辟dp数组
int *initDP(int n) {
    int *dp = (int *)malloc(sizeof(int) * (n + 1));
    int i;
    for(i = 0; i <= n; ++i)
        dp[i] = 0;
    return dp;
}

int numTrees(int n){
    //开辟dp数组
    int *dp = initDP(n);
    //将dp[0]设为1
    dp[0] = 1;

    int i, j;
    for(i = 1; i <= n; ++i) {
        for(j = 1; j <= i; ++j) {
            //递推公式：dp[i] = dp[i] + 根为j时左子树种类个数 * 根为j时右子树种类个数
            dp[i] += dp[j - 1] * dp[i - j];
        }
    }

    return dp[n];
}