【高等数学之极限】

发布时间：2024年01月19日

一、引言?

在开始本节之前我们先来看三个小题目:

请问以上三式可以将极限值带入吗?

当然我们清楚，在求极限之前要先判断整个式子的形式，上面以及给出答案了，(1)是可以直接带入求值的，它并不是我们所熟知的任一未定形式，那我们又出现问题了，为什么(1)可以直接转换成上下两个式子分别求极限，那这就涉及到我们的极限四则运算法则了:

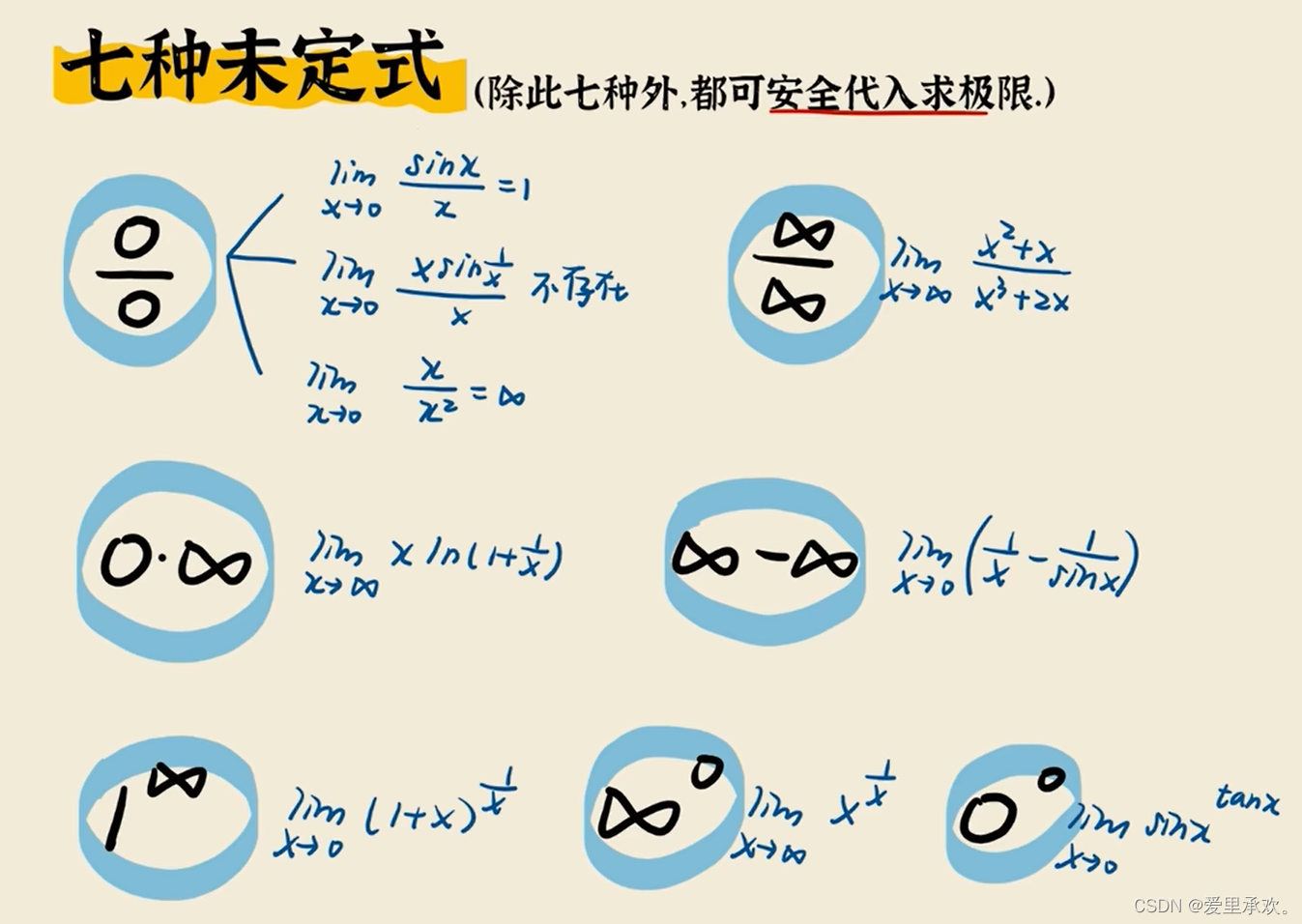
那么我们再看(2)(3)，可以发现将极限值带入后，表达式是我们上面总结的七种未定式之一，那我们就要用特殊的方法来求解了。

二、等价无穷小

等价无穷小代换也是我们求解极限问题非常好用的一个办法，我们要记住上述的等价代换。

其实上面也是利用了极限的四则运算而已。

三、拆极限

其实，综上所诉，拆极限也就是要保证:

四、提前求极限

那什么叫提前求极限呢?也就是说将极限的趋向值在化简之前提前代入表达式的一部分提前求出值，以起到约分化简式子的目的。

五、洛必达法则

"洛神"也是有一定的使用条件的，大家一定要擦亮双眼哦!

六、特殊类型的极限

6.1、方法一?

6.2、方法二?

文章来源:https://blog.csdn.net/zhhdbehx/article/details/135700635
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章