12.18构建哈夫曼树(优先队列),图的存储方式,一些细节(auto,pair用法,结构体指针)
为结构体自身时,用.调用成员变量;为结构体指针时,用->调用成员变量
所以存在结构体数组时,调用数组元素里的成员变量,就是要用.
结构体自身只有在new时才会创建出来,而其指针可以随意创建
在用new时,要返回指向结构体的指针
构建哈夫曼树
哈夫曼树是在叶子节点和权重确定的情况下,带权路径最小的二叉树,也被称为最优二叉树
基本思路就是先将每个给定权值的节点看成一颗只有根节点的树,然后不断合成权值最小的两个树,生成一个权值为他们之和的一颗新树,最终剩下的一棵树就是哈夫曼树
如果有N个节点,就要迭代N-1轮
优先队列

注意队列的队头函数是front,优先队列是top,栈也是top
大顶堆是一种特殊的二叉堆,其中每个父节点的值都大于或等于其子节点的值。因此,大顶堆是按照降序排列的,即根节点的值最大,而子节点的值逐渐减小。
//升序队列
priority_queue <int,vector<int>,greater<int> > q;
//降序队列
priority_queue <int,vector<int>,less<int> >q;
//greater和less是std实现的两个仿函数(就是使一个类的使用看上去像一个函数。其实现就是类中实现一个operator(),这个类就有了类似函数的行为,就是一个仿函数类了)?
即需要注意优先队列的第三个参数传入的并不是函数,而是一个结构体
?? ?priority_queue<int, vector<int>, less<int>>a;//定义了降序排列的优先队列,即队头最大,从队头到队尾逐渐减小
?? ?priority_queue<int, vector<int>, greater<int>>a;//小顶堆,从队头到队尾升序排列
第二个参数只用写类型即可
struct tmp1 {
int x;
tmp1(int a) { x = a; }//:x(a){}
bool operator<(const tmp1& a)const {
return x < a.x;
}
};//运算符重载
//这里就是直接在存储的类型里,然后重载运算符,这个调用优先队列时,只需要一个参数,即要存储的结构体即可
//因为结构体里就已经包装了比较的方法
struct tmp2 {
bool operator()(tmp1 a, tmp1 b) {
return a.x < b.x;
}
};//写仿函数,就是写一个比较函数,不过是包装成结构体,
//需要注意这里是额外写的一个结构体,所以在优先队列里定义的时候,要第三个参数,写到第三个参数里
//然后第一个参数是存储的类型,第二个是vector<相应类型>,表示存储的容器在STL中,如果你使用的是标准的std::priority_queue容器,那么需要定义的仿函数的确是要重载函数调用运算符operator(),因为std::priority_queue默认使用std::less或std::greater作为仿函数,它们都是通过重载函数调用运算符来实现比较的。
即写仿函数时,只能重载运算符()
这个第三个参数就是代表从队头到队尾满足一个怎样的关系。队头就是堆顶元素
为什么less构建出大顶堆
想的是类似于自定义sort排序方式,排序都按照规定的<与>方向进行排序
但优先队列相反,用<时,头部是最大的;用>时,头部是最小的
根因在于其底层实现。
less:左数小于右数时,返回true,否则返回false。
在堆的调整过程中,对于大顶堆,如果当前插入的节点值大于其父节点,那么就应该向上调整。其父节点索引小于当前插入节点的索引,也就是父节点是左数,插入节点是右值,可以看到,左数小于右数时,要向上调整,也就是Compare函数应该返回true,正好是less。
(而对于顺序存储,左数右数就是直观理解,没有固定,这里是堆,所以就固定先前的位置为左数,要比较的是右数,如果先前固定的位置和比较的位置满足关系,就要交换,返回true不然则不动)
priority_queue传入的第三个参数是仿函数,是将新插入数据与父结点进行比较
原本是:if (_con[child] > _con[parent])
使用仿函数:if (com(_con[child] , _con[parent]))
(调用仿函数是这个形式,所以仿函数结构体里只能重载())
这里记住,是将父结点与子结点进行比较,满足条件(置true才进行交换)就很容易记住哪个对应大顶堆,哪个对应小顶堆了
就是说仿照堆的构建过程,新插入的直接和最大的比较,而不是连续的顺序存储,从小比到大,类似于插入排序
细节
只有string为length
返回数据结构的大小用的都是size(),只有string类用的是Length()?
数对pair
vector可以存储数对,但对于数对,必须要在数对<>前标明pair,直接写为这样会报错

应该写为

auto的应用
auto返回的就是数据结构内部储存的数据的类型

?????for 循环后的括号由冒号“?:”分为两部分:第一部分是范围内用于迭代的变量,第二部分则表示被迭代的范围。?
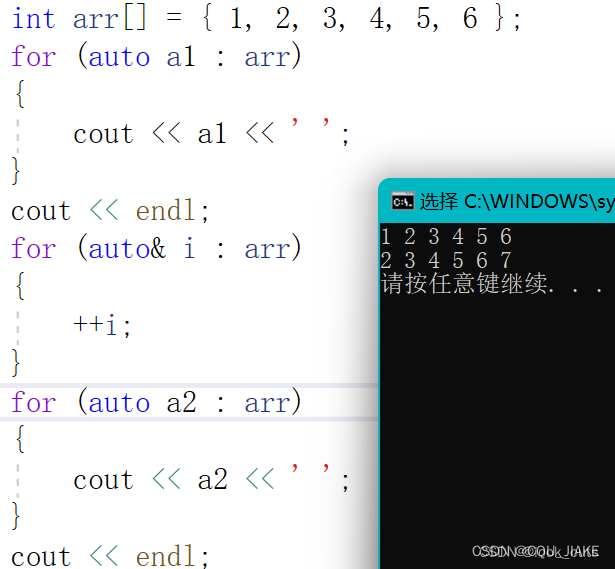
std::map<std::string, int> scores = {{"Alice", 90}, {"Bob", 80}, {"Charlie", 95}};
for (auto it = scores.begin(); it != scores.end(); ++it) {
auto& name = it->first;
auto& score = it->second;
// 使用 name 和 score 进行操作
}
?
huf* root = bulid(weights, chars);
vector<hfcode>code;
generatecod(root, "", code);
for (auto hc : code) {
cout << hc.ch << " : " << hc.code << endl;
}总代码
struct huf {
int w;
char ch;
huf* left, * right;
huf(int w, char c = '\0', huf* l = nullptr, huf* r = nullptr) :w(w), ch(c), left(l), right(r) {}
};
struct hfcode {
char ch;//ch是原本的字符值
string code;//这个是编码后的结果
//本质上就是一个pair对
hfcode(char c = '\0', string s = "") :ch(c), code(s) {}
};
struct cmp {
bool operator()(huf* a, huf* b) { return a->w > b->w; }
};//如果大于了就交换,返回true,说明新换上来的比较小,那么堆顶元素就保持为最小的
huf* build(vector<int>& weights, vector<char>& chars) {
priority_queue<huf*, vector<huf*>, cmp>pq;
for (int i = 0; i < weights.size(); i++) {
pq.push(new huf(weights[i], chars[i]));
}
while (pq.size() > 1) {
huf* left = pq.top();
pq.pop();
huf* right = pq.top();
pq.pop();
huf* parent = new huf(left->w + right->w, '\0', left, right);
pq.push(parent);
}
return pq.top();
}
void generatecod(huf* root, string code, vector<hfcode>& hufcode) {//目的是要得到每个叶子节点的哈夫曼编码,这个vecotr数组记录的是hfcode结构体,就是原始数据以及编码的一个数对
if (!root)return;
if (root->ch != '\0') {//如果是\0就表明是非叶子节点,不是就表明是叶子节点,是需要编码的节点,所以就进行
hufcode.push_back(hfcode(root->ch, code));
}
generatecod(root->left, code + "0", hufcode);
generatecod(root->right, code + "1", hufcode);
}
vector<int>weights = { 5,2,7,4,9 };
vector<char>chars = { 'A', 'B', 'C', 'D', 'E' };
huf* root = bulid(weights, chars);
vector<hfcode>code;
generatecod(root, "", code);
for (auto hc : code) {
cout << hc.ch << " : " << hc.code << endl;
}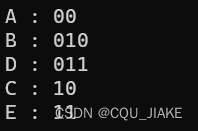 ?
?
#include<iostream>
#include<queue>
#include<vector>
#include<string>
using namespace std;
struct node {
int w;//表示节点的权重,为叶子节点时表示出现的频次
char ch;//表示节点的编号,名称
node* left, * right;
node(int w, char c = '\0', node* l = nullptr, node* r = nullptr) :w(w), ch(c), left(l), right(r) {}
//含参,默认,构造函数,c为\0时表示非叶子节点,无实际意义,w为不含参,需要实际传值
};
struct cmp {
bool operator()(node* a, node* b) {
return a->w < b->w;
}
};
node* build(vector<int>ws, vector<char>cs) {
priority_queue<node*, vector<node*>, cmp>pq;
for (int i = 0; i < ws.size(); i++) {
node* n = new node(ws[i], cs[i]);
pq.push(n);//将所有的叶子节点加入到优先队列当中
}
while (pq.size() > 1) {
node* l = pq.top();
pq.pop();
node* r = pq.top();
pq.pop();
node* parent = new node(l->w + r->w, '\0', l, r);
pq.push(parent);
}
return pq.top();//最后返回构建好的哈夫曼树的根节点指针
}
void code(node* root, string c, vector <pair< char, string >> &a) {
if (!root)return;
if (root->ch != '\0') {
a.push_back(make_pair(root->ch, c));
}
else {
code(root->left, c + '0', a);
code(root->right, c + '1', a);
}
}
int main() {
vector<int>w = { 5,2,7,4,9 };
vector<char>chars = { 'A', 'B', 'C', 'D', 'E' };
node* root = build(w, chars);
vector<pair<char, string>>d;
code(root, "", d);
for (auto dp : d) {
cout << dp.first << ":" << dp.second << endl;
}
return 0;
}
调试过程
vector<int>webuild = { 5,2,7,4,9 };
vector<char>chars = { 'A', 'B', 'C', 'D', 'E' };
priority_queue < pair<int, char>, vector<pair<int, char>>, cmp1>p;
for (int i = 0; i < weights.size(); i++) {
p.push(make_pair(weights[i], chars[i]));
}
while (!p.empty()) {
cout << p.top().second << ":" << p.top().first << endl;
p.pop();
}struct cmp1 {
bool operator()(pair<int, char>a, pair<int, char>b) {
return a.first < b.first;
}
};图的存储方式
struct arc {
int target;//边里需要记录自己的目标
arc* nextarc;
int w;//如果有需要,则记录边的权重
};
struct node {
int info;//并非节点编号,而是节点自身的某些信息,比如名称,大小
arc* firstarc;
};
struct graph {
int vnum, anum;
node v[20];//在此定义节点编号
};
void creat(graph& g) {
cin >> g.vnum >> g.anum;
for (int i = 0; i < g.vnum; i++) {
cin >> g.v[i].info;//按输入顺序定义节点编号
g.v[i].firstarc = nullptr;
}
for (int i = 0; i < g.anum; i++) {
int v1, v2;
cin >> v1 >> v2;
arc* p1 = new arc;
p1->target = v2;
p1->nextarc = g.v[v1].firstarc;
g.v[v1].firstarc = p1;
//若为无向图,还需在v2中做修改
arc* p2 = new arc;
p2->target = v1;
p2->nextarc = g.v[v2].firstarc;
g.v[v2].firstarc = p2;
}
}边要记录自己的终点,以及同一起点下边的下一边的索引指针,需要的话还可以记录权值;
边记录的终点,是终点节点的下标标号;点记录的边,是第一条边的索引指针
点要记录以自己为起点的第一条边的索引指针,若要遍历以该边为起点的所有边,用第一条边的后继指针来实现
得到每个点的入度
struct arc {
int w;
int target;
arc* nextarc;
};
struct node {
int index;
arc* firstarc;
};
struct graph {
int vnum, anum;
node v[20];
};
int d[20];//记录入度
void countd(graph& g) {//i表示要查询的节点编号
for (int i = 0; i < g.vnum; i++) {
d[i] = 0;
}
for (int i = 0; i < g.vnum; i++) {
for (arc* item = g.v[i].firstarc; item != nullptr; item = item->nextarc) {
d[item->target]++;
}
}
}本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Wireshark在移动网络中的应用
- FCA 指控个人实施 1900 万英镑的投资欺诈计划
- 【PotatoAdmin】系统的设计记录(未完结)
- JavaScript中作用域的理解
- 32.virtual reality system concepts illustrated using OSVR
- GAMES101-Assignment2
- 学生选课系统02 用户故事、流程图、业务流程图
- 如潮好评!优秀选手视角下的第二届粤港澳大湾区(黄埔)国际算法算例大赛
- Midjourney NIJI5制作动漫风格作品保姆级教程
- Java stream&File