C语言数据结构-----二叉树(3)二叉树相关练习题

前言

前面详细讲述了二叉树的相关知识，为了巩固，做一些相关的练习题

---

在做题之前，需要补充二叉树的一条性质：对任何一棵二叉树, 如果度为0其叶结点个数为n₀ , 度为2的分支结点个数为n₂ ,则有：
n₀＝n₂ ＋1

1.某二叉树共有 399 个结点，其中有 199 个度为 2 的结点，则该二叉树中的叶子结点数为？

A 不存在这样的二叉树
B 200
C 198
D 199

解析：B
叶子节点即为度为0的节点，由性质可知，叶子结点数=199+1=200

2.下列数据结构中，不适合采用顺序存储结构的是？

A 非完全二叉树
B 堆
C 队列
D 栈

解析：A

3.在具有 2n 个结点的完全二叉树中，叶子结点个数为？

A n
B n+1
C n-1
D n/2

解析：A

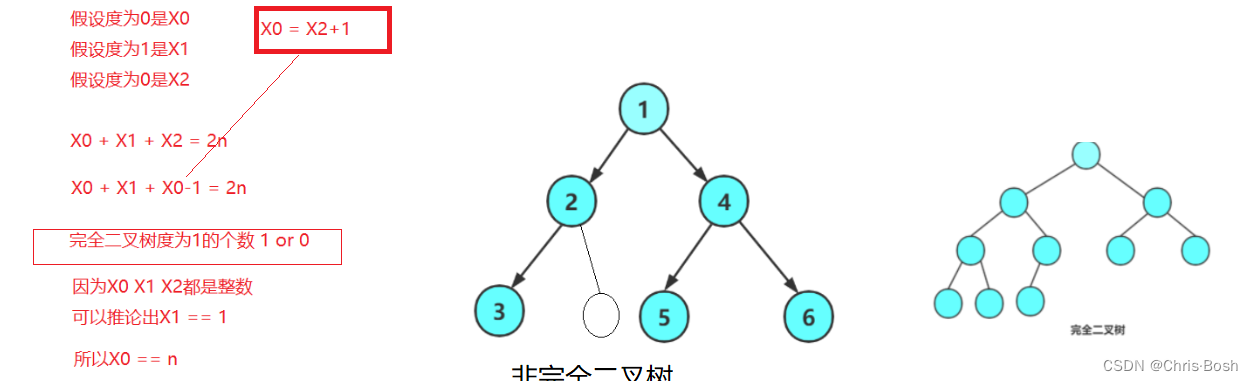
4.一棵完全二叉树的节点数位为531个，那么这棵树的高度为？

A 11
B 10
C 8
D 12

解析：B

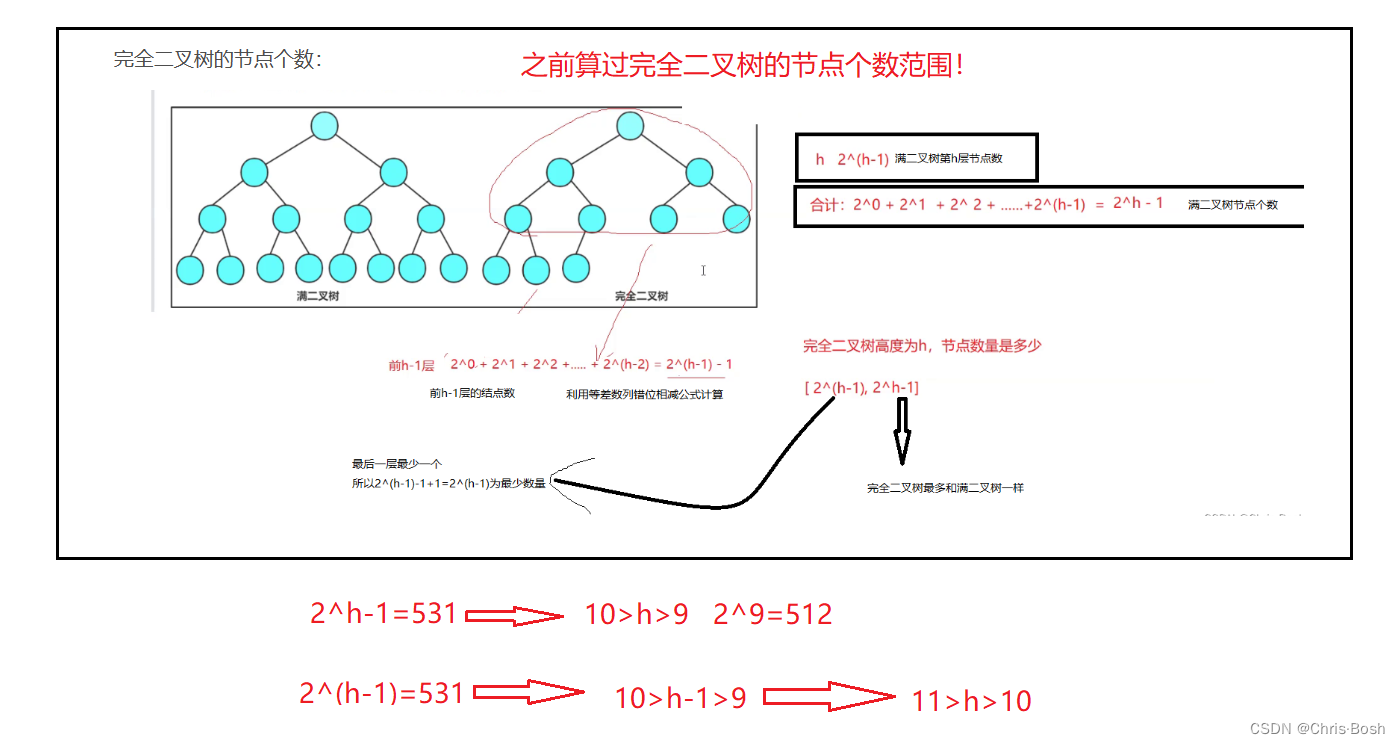
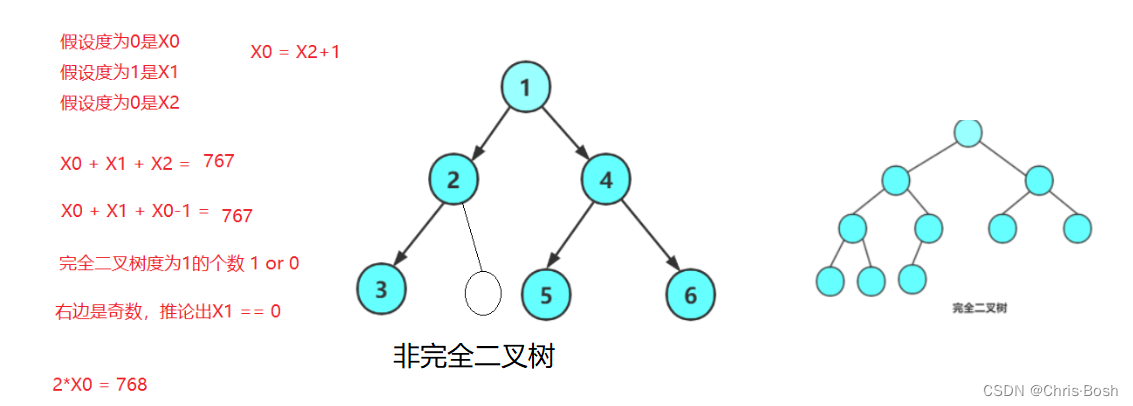
5.一个具有767个节点的完全二叉树，其叶子节点个数为？

A 383
B 384
C 385
D 386

解析：B

6.单值二叉树

bool isUnivalTree(struct TreeNode* root) 
{
    if (root==NULL)
    return true;
    if (root->left!=NULL&&root->left->val!=root->val)
    return false;
    if (root->right!=NULL&&root->right->val!=root->val)
    return false;
    return isUnivalTree(root->left)&&isUnivalTree(root->right);
}

解析：
如果树为空，那么并不违反规则。
如果树的左边不为空，并且左边的值不等于root的值那么错误。右边同理。
最后对左子树和右子树递归调用！

7.相同的树

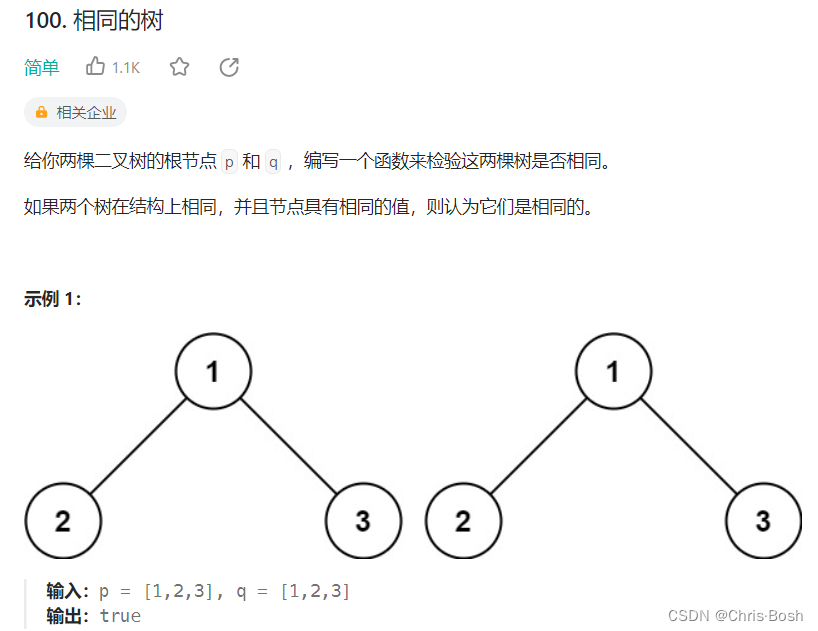
bool isSameTree(struct TreeNode* p, struct TreeNode* q) 
{
    if (p==NULL&&q==NULL)
    return true;
    if (p==NULL&&q!=NULL)
    return false;
    if (q==NULL&&p!=NULL)
    return false;
    if (p->val!=q->val)
    return false;

    return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}

解析：先把几种特殊情况写了，就是pq都为空，p空q不空，q空p不空，pq都不空但值不相等。
写完了几种特殊情况就可以递归左子树和右子树判断了！

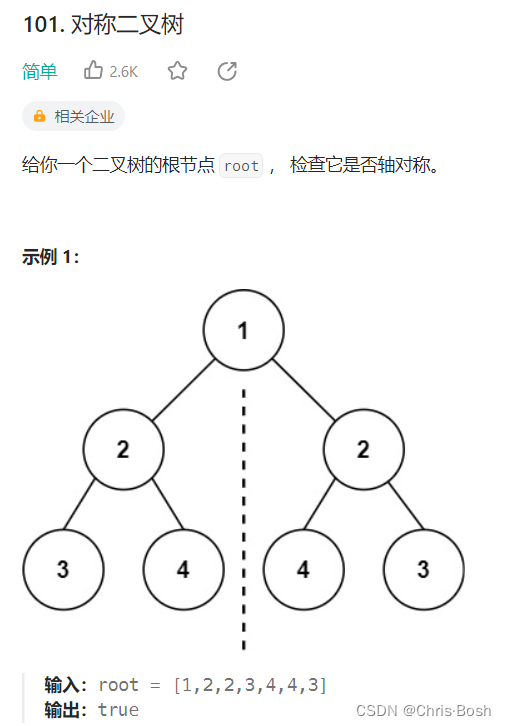
8.对称二叉树

bool doubleisSymmetric(struct TreeNode* root1,struct TreeNode* root2) 
{
    if (root1==NULL&&root2==NULL)
    return true;
    if (root1==NULL||root2==NULL)
    return false;
    if (root1->val!=root2->val)
    return false;

    return doubleisSymmetric(root1->left,root2->right)&&doubleisSymmetric(root1->right,root2->left);
}

bool isSymmetric(struct TreeNode* root)
{
    return doubleisSymmetric(root->left,root->right);
}

解析

9.二叉树的最大深度

int maxDepth(struct TreeNode* root)
{
    return (root==NULL)?0:fmax(maxDepth(root->left),maxDepth(root->right))+1;
}

解析：
用一个三目就可以解决，如果为空深度就为0，否则的话遍历左子树和右子树遍历一次+1，一直到底，左边和右边谁打谁就是深度。

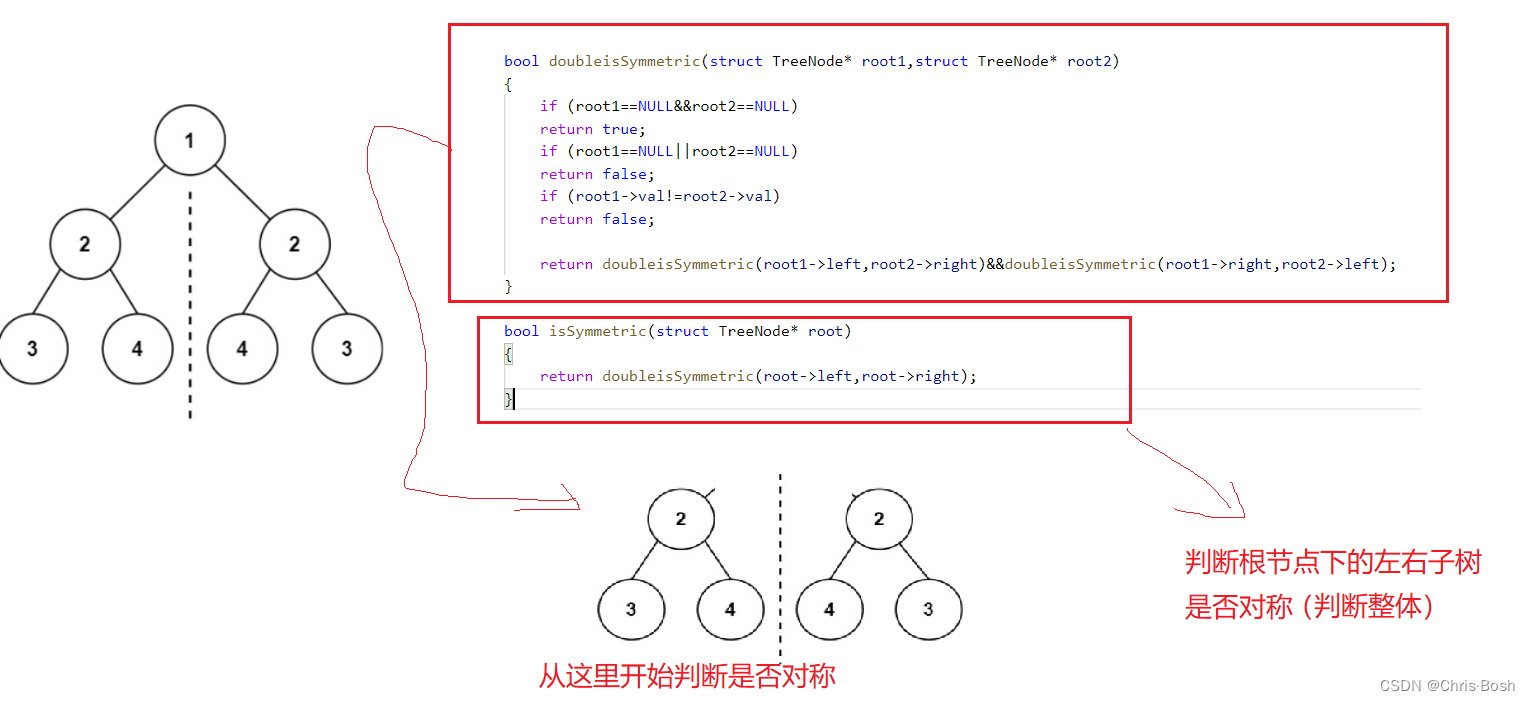
10.另一棵树的子树

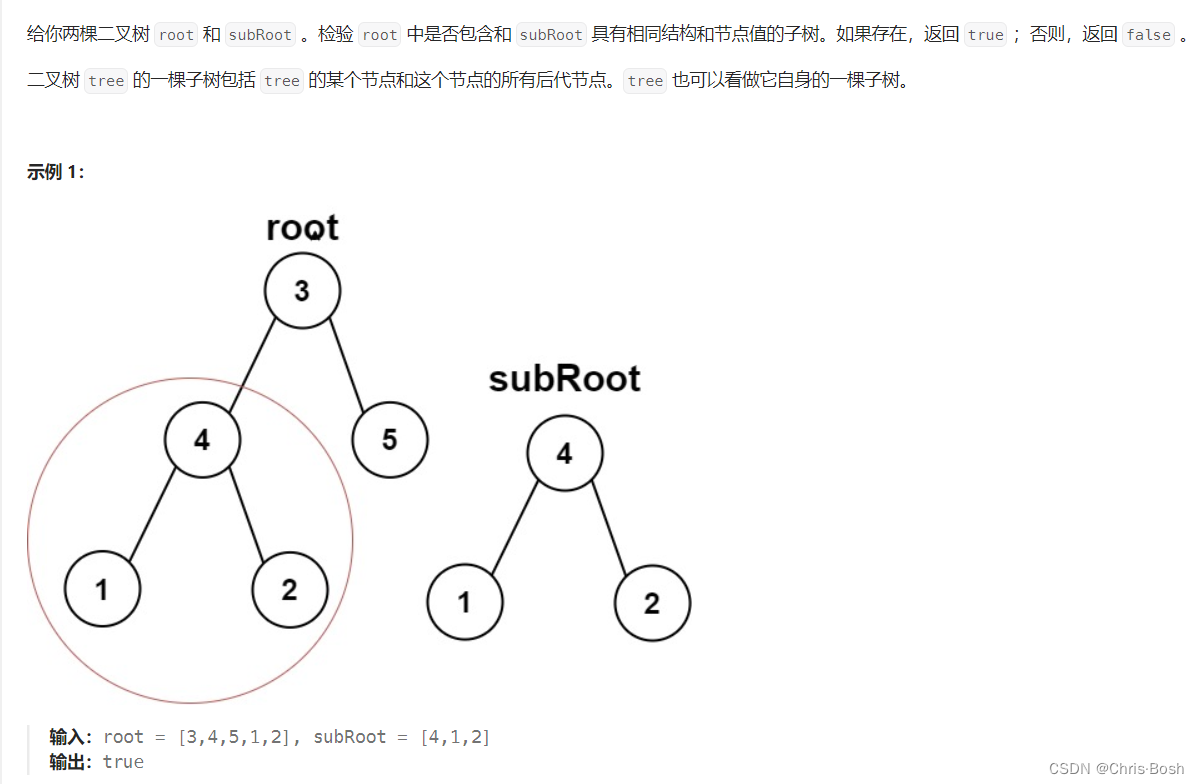
bool isSameTree(struct TreeNode* p, struct TreeNode* q) 
{
    if (p==NULL&&q==NULL)
    return true;
    if (p==NULL||q==NULL)
    return false;
    if (p->val!=q->val)
    return false;

    return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
    if(root==NULL)
    return false;
    
    if (root->val==subRoot->val)
    {
        if (isSameTree(root,subRoot))
        return true;
    }

    return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
}

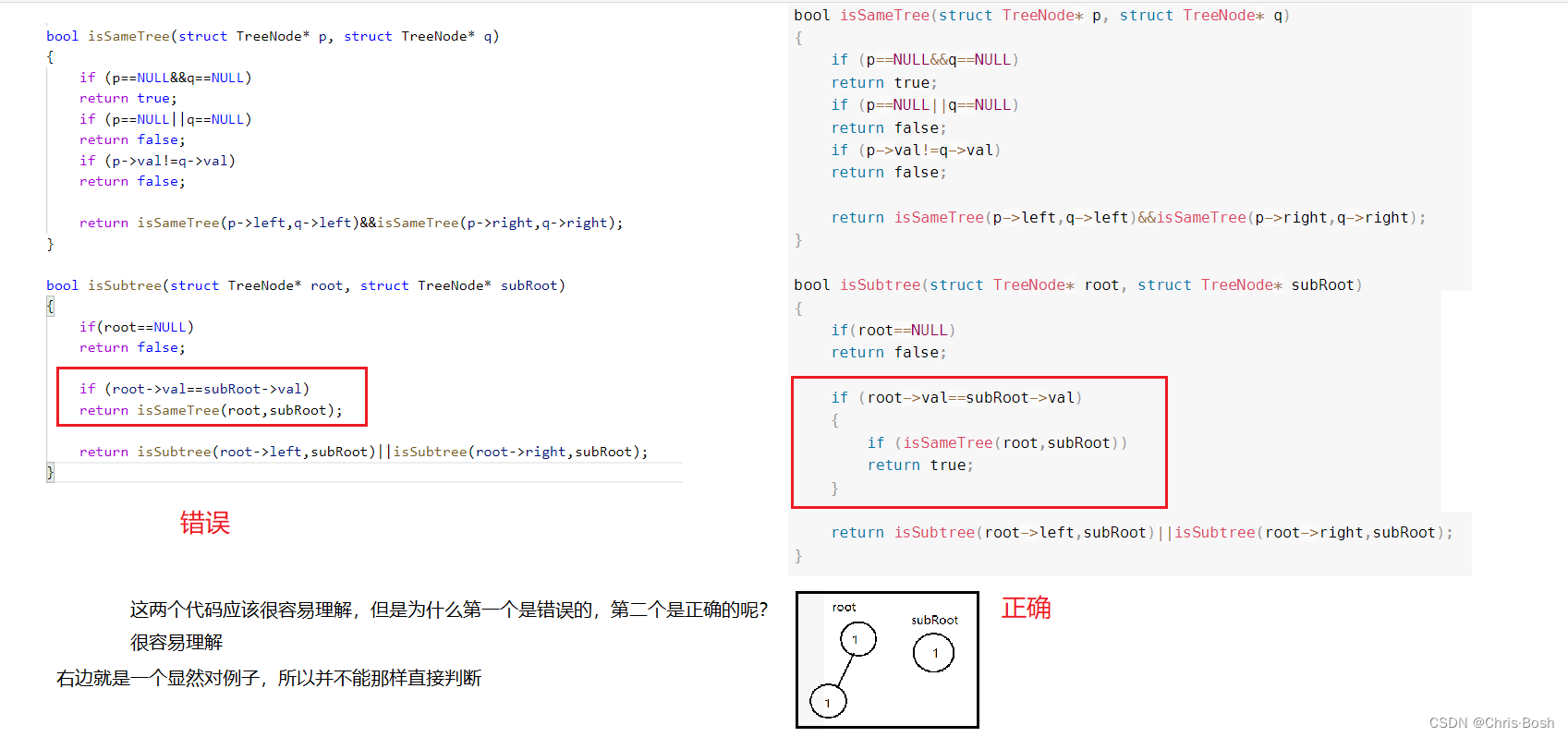
11.翻转二叉树

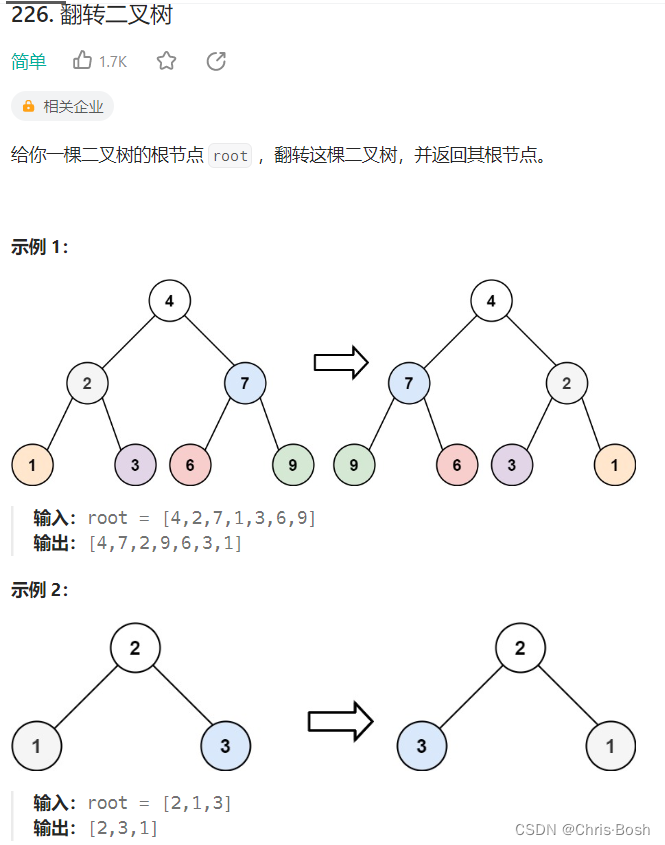
第一次写是这样的，但是发现这样写麻烦了，没必要直接写个swap函数，还调用二级指针麻烦！

void swap(struct TreeNode** a, struct TreeNode** b) {
    struct TreeNode* temp = *a;
    *a = *b;
    *b = temp;
}

struct TreeNode* invertTree(struct TreeNode* root) {
    if (root == NULL)
        return NULL;
    
    swap(&(root->left), &(root->right));
    
    invertTree(root->left);
    invertTree(root->right);
    
    return root;
}

修改一下，看着简单舒服多了

struct TreeNode* invertTree(struct TreeNode* root) 
{
        if (root == NULL) 
        return NULL;
         struct TreeNode* temp;
        temp=root->left;
        root->left=root->right;
        root->right=temp;
        invertTree(root->left);
        invertTree(root->right);
        return root;
}

到这里，这个级别的代码就应该不需要解析了吧，都能看懂。

12.二叉树的前序遍历

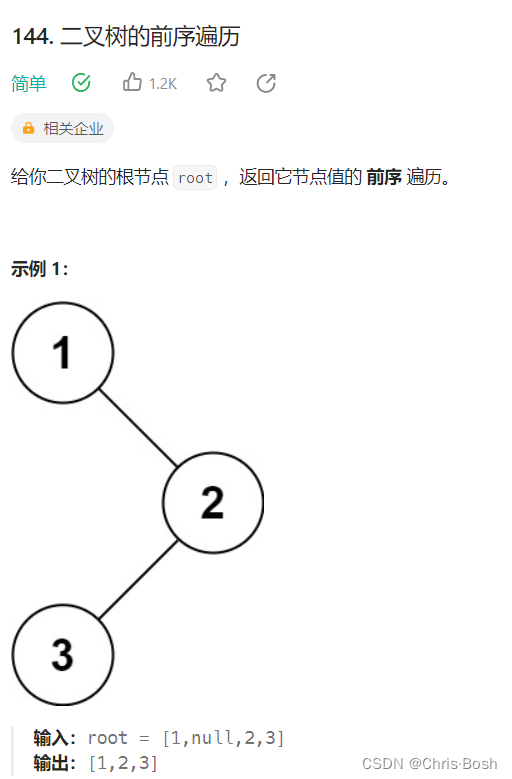
void preorder(struct TreeNode* root, int* res, int* resSize) 
{
    //root：当前节点的指针。
    //res：存储遍历结果的数组。
    //resSize：指向遍历结果数组元素个数的指针。
    if (root == NULL) 
        return;
    res[(*resSize)++] = root->val;
    preorder(root->left, res, resSize);
    preorder(root->right, res, resSize);
}

int* preorderTraversal(struct TreeNode* root, int* returnSize)
{
    int* res = malloc(sizeof(int) * 2000);
    *returnSize = 0;
    preorder(root, res, returnSize);
    return res;
}

12.1 二叉树的中序遍历

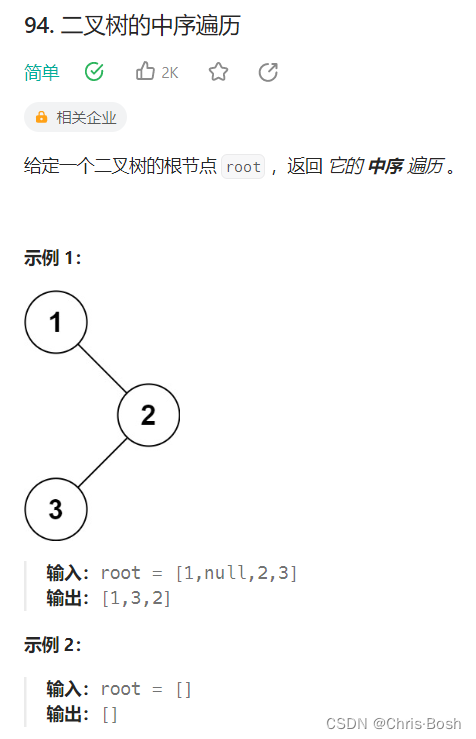
void inorder(struct TreeNode* root, int* res, int* resSize) 
{
    //root：当前节点的指针。
    //res：存储遍历结果的数组。
    //resSize：指向遍历结果数组元素个数的指针。
    if (root == NULL) 
        return;
    inorder(root->left, res, resSize);
      res[(*resSize)++] = root->val;
    inorder(root->right, res, resSize);
}

int* inorderTraversal(struct TreeNode* root, int* returnSize) 
{
    int* res = malloc(sizeof(int) * 2000);
    *returnSize = 0;
    inorder(root, res, returnSize);
    return res;
}

12.2 二叉树的后序遍历

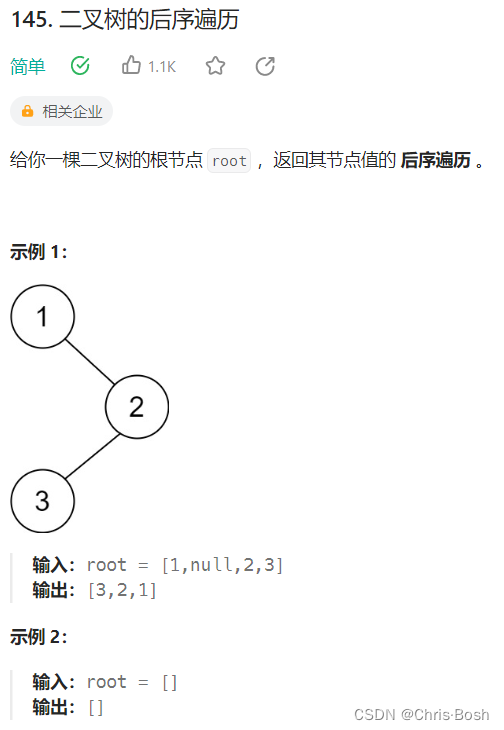
void postorder(struct TreeNode* root, int* res, int* resSize) 
{
    //root：当前节点的指针。
    //res：存储遍历结果的数组。
    //resSize：指向遍历结果数组元素个数的指针。
    if (root == NULL) 
        return;
    postorder(root->left, res, resSize);
    postorder(root->right, res, resSize);
    res[(*resSize)++] = root->val;
}

int* postorderTraversal(struct TreeNo
de* root, int* returnSize) 
{
     int* res = malloc(sizeof(int) * 2000);
    *returnSize = 0;
    postorder(root, res, returnSize);
    return res;
}

这三道题如出一辙，所以我把他们放到一起。代码都很简单，大家应该都能看懂！

13.平衡二叉树

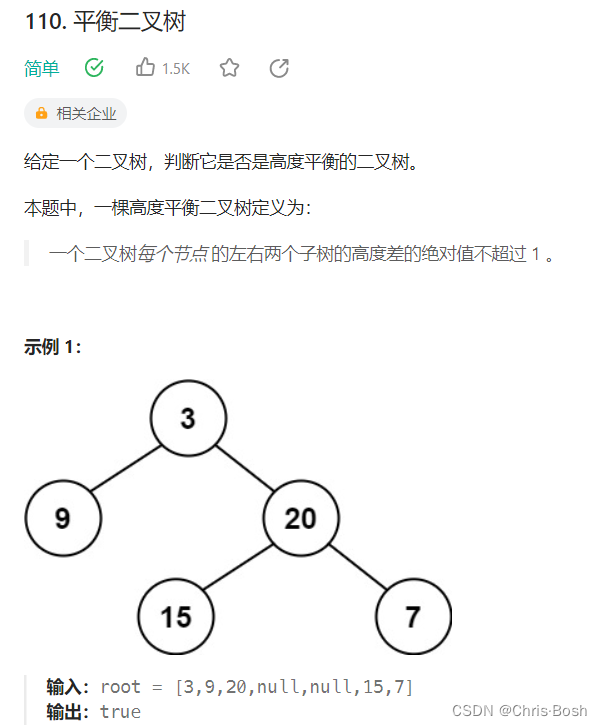
int TreeHeight(struct TreeNode* root)
{
	if (root == NULL)
		return 0;
	int leftHeight = TreeHeight(root->left);
	int rightHeight = TreeHeight(root->right);

	return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}


bool isBalanced(struct TreeNode* root) 
{
    	if (root == NULL)
		return true;
        else 
        return fabs(TreeHeight(root->left) - TreeHeight(root->right)) <= 1 
        && isBalanced(root->left) 
        && isBalanced(root->right);
}

解析:
先求二叉树的左高度和右高度，然后递归返回来判断是否满足题意。

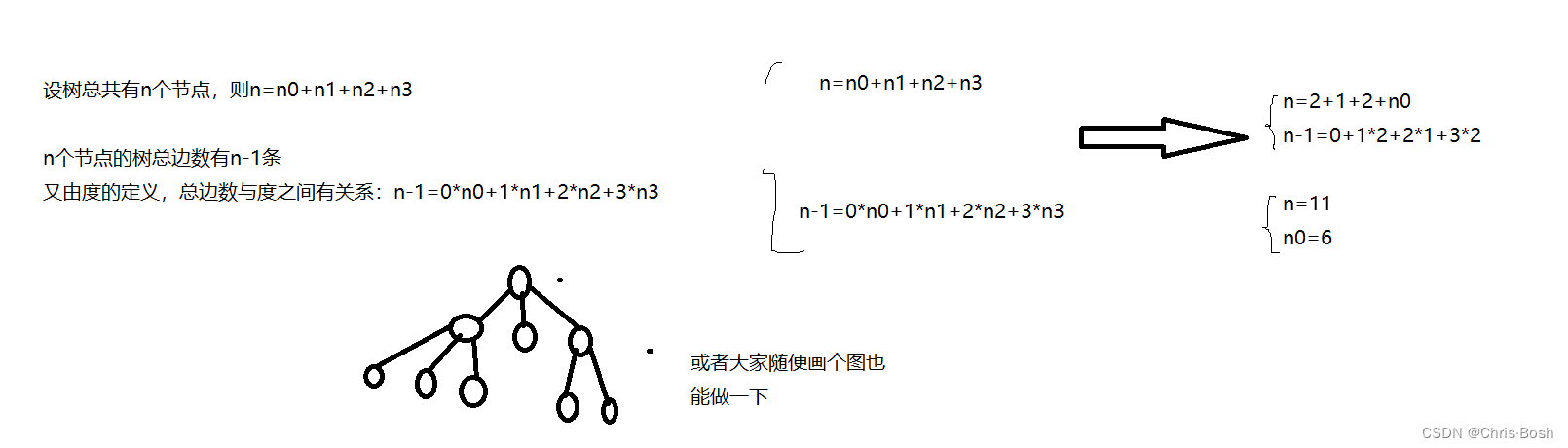
14.在一颗度为3的树中，度为3的结点有2个，度为2的结点有1个，度为1的结点有2个，则叶子结点有（ ）个

A.4
B.5
C.6
D.7

解析：C

15.设根结点的深度为1，则一个拥有n个结点的二叉树的深度一定在（ ）区间内

A.[log(n + 1)，n]
B.[logn，n]
C.[log(n + 1)，n - 1]
D.[log(n + 1)，n + 1]

解析：

最大深度： 即每次只有一个节点，次数二叉树的高度为n，为最高的高度
最小深度： 此树为完全二叉树， 如果是完全二叉树
根据二叉树性质，完全二叉树的高低为 h = log(n+1)向上取整

故答案为 [log(n + 1)，n]

16.一颗完全二叉树有1001个结点，其叶子结点的个数是（ ）

A.251
B.500
C.501
D.不能确定

解析：C

完全二叉树的最后一个结点的编号一定是1001，则它的父结点的编号为1001/2=500，则叶子结点个数为1001-500=501.
总结一下：完全二叉树的最后一个结点的编号是n，则它的父结点的编号为[n/2]，则叶子结点个数为n-[n/2]。

17.一颗拥有1000个结点的树度为4，则它的最小深度是（ ）

A.5
B.6
C.7
D.8

解析：B
如果这棵树每一层都是满的，则它的深度最小，假设它为一个四叉树，高度为h，则这个数的节点个数为(4^h - 1) / 3，当h = 5, 最大节点数为341， 当h = 6, 最大节点数为1365，所以最小深度应该为6。

18.如果一颗二叉树的前序遍历的结果是ABCD，则满足条件的不同的二叉树有（ ）种

A.13
B.14
C.15
D.16

解析：B

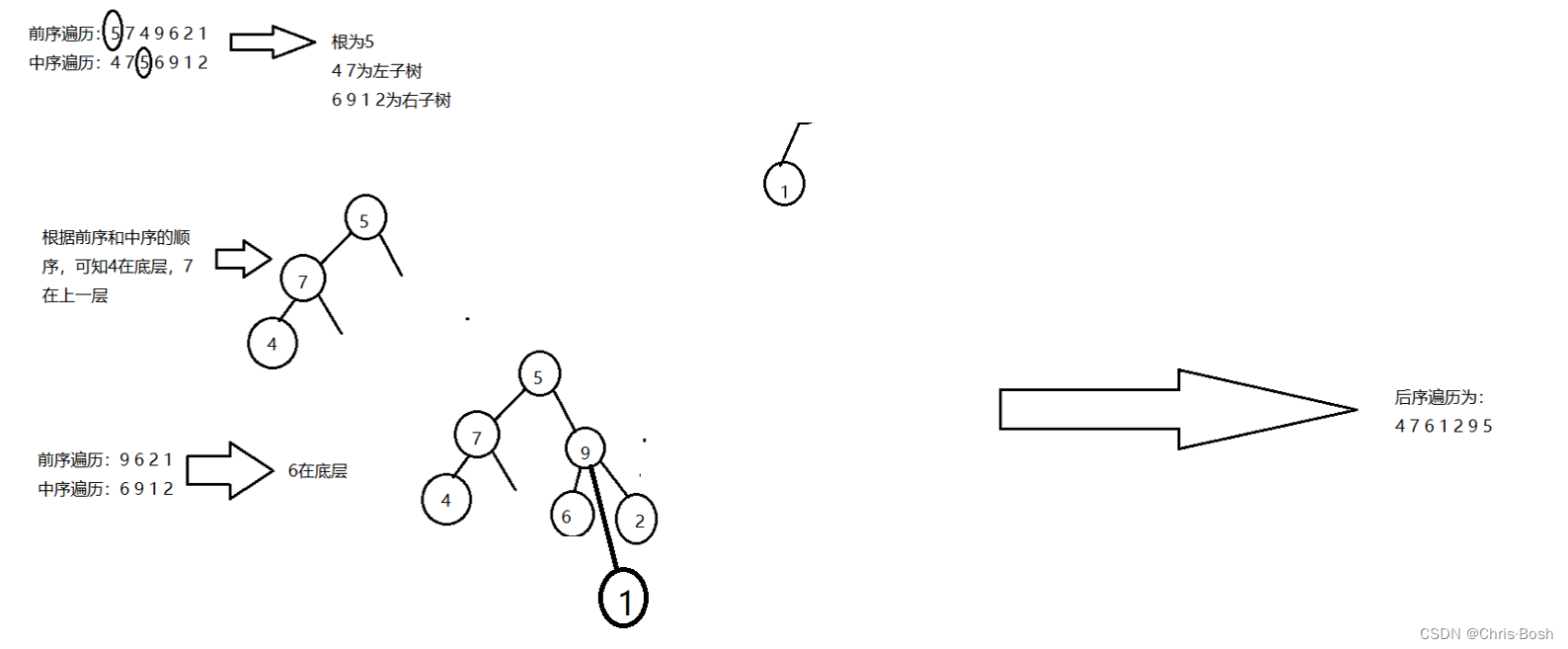
19.已知某二叉树的前序遍历序列为5 7 4 9 6 2 1，中序遍历序列为4 7 5 6 9 1 2，则其后序遍历序列为（ ）

A.4 2 5 7 6 9 1
B.4 2 7 5 6 9 1
C.4 7 6 1 2 9 5
D.4 7 2 9 5 6 1

解析：C

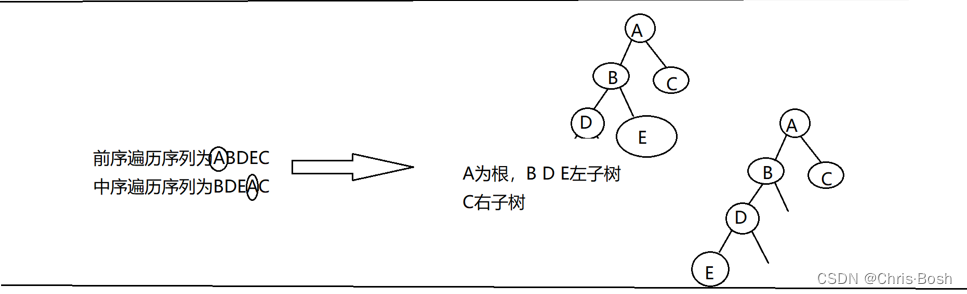
20.已知某二叉树的前序遍历序列为ABDEC，中序遍历序列为BDEAC，则该二叉树（ ）

A.是满二叉树
B.是完全二叉树，不是满二叉树
C.不是完全二叉树
D.是所有的结点都没有右子树的二叉树

解析：感觉有两种情况 B,C

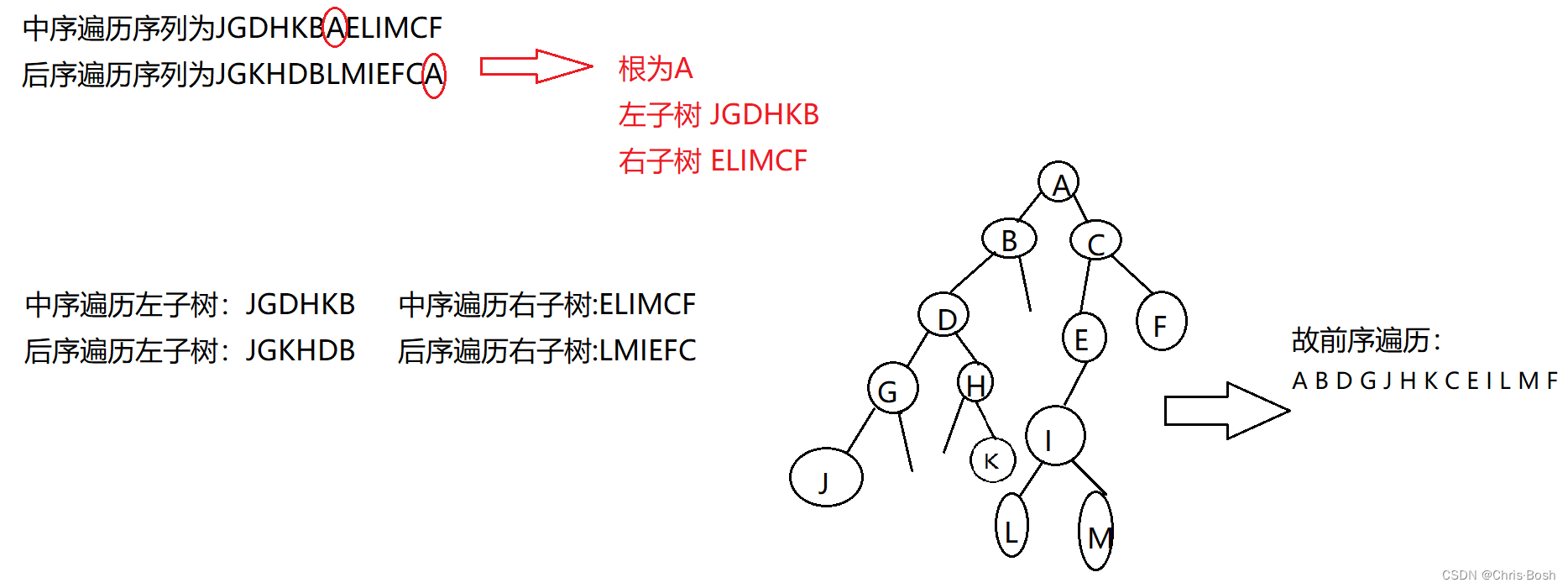
21.已知某二叉树的中序遍历序列为JGDHKBAELIMCF，后序遍历序列为JGKHDBLMIEFCA，则其前序遍历序列为（ ）

A.ABDGHJKCEFILM
B.ABDGJHKCEILMF
C.ABDHKGJCEILMF
D.ABDGJHKCEIMLF

解析：B