Lagrange对偶法

发布时间：2024年01月12日

这里写自定义目录标题

Lagrange dual
上海交通大学 CS257 Linear and Convex Optimization
南京大学 Duality (I) - NJU

the standard form (5.1)
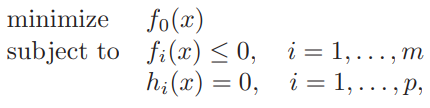
在这里插入图片描述
min ? X ???? f ( X ) s . t . ?? g i ( X ) ≤ 0 , ? i = 1 , … , m , \begin{array}{l} {\mathop {\min }_{\bf{X}} \;\;f\left( {\bf{X}} \right)}\\ {{\rm{s}}.{\rm{t}}.\;{g_i}\left( {\bf{X}} \right) \le 0,\forall i = 1, \ldots ,m,} \end{array} minX?f(X)s.t.gi?(X)≤0,?i=1,…,m,?

5.1.1 The Lagrangian

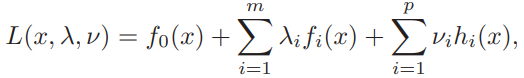
在这里插入图片描述
the dual variables or Lagrange multiplier vectors associated with the problem (5.1).

5.1.2 The Lagrange dual function

the minimum value of the Lagrangian
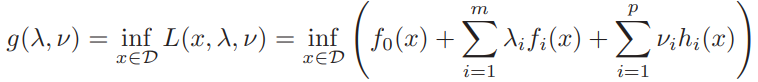
在这里插入图片描述

5.2 The Lagrange dual problem

the Lagrange dual problem associated with the problem (5.1).
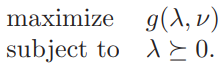
在这里插入图片描述

5.2.3 Strong duality and Slater’s constraint qualification

在这里插入图片描述

5.2.3 Strong duality and Slater’s constraint qualification

Slater’s theorem states that
strong duality holds, if Slater’s condition holds (and the problem is convex).
strong duality obtains, when the primal problem is convex and Slater’s condition holds

Slater’s Condition for Convex Problems
上海交通大学 CS257 Linear and Convex Optimization
在这里插入图片描述

5.5.3 KKT optimality conditions

Karush-Kuhn-Tucker (KKT) conditions
在这里插入图片描述
for any optimization problem with differentiable objective and constraint functions for which strong duality obtains, any pair of primal and dual optimal points must satisfy the KKT conditions (5.49).

在这里插入图片描述

文章来源:https://blog.csdn.net/qq_42806204/article/details/135554028
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章